【摘要】：对应于这些分岔点，在上面的幅频响应曲线中存在相应的环面分岔点，同时稳定周期运动通过这些分岔失去其稳定性，从而导致弹性地基梁的拟周期运动。为了证明这些拟周期运动的存在，接下来利用Runge-Kutta法对离散化模型直接进行相应的数值积分。图6.7给出柔性地基梁当p=0.10时的非周期运动，其中Ω/ω1=1.005。
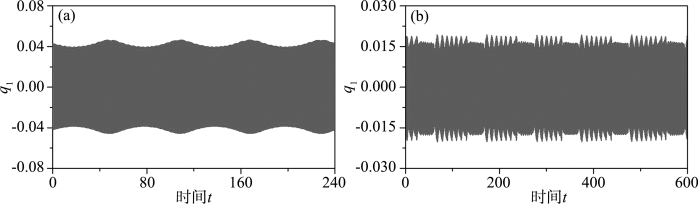
在第5章中的摄动分析已经预测了在共振区内的Hopf分岔点。对应于这些分岔点，在上面的幅频响应曲线中存在相应的环面分岔点，同时稳定周期运动通过这些分岔失去其稳定性，从而导致弹性地基梁的拟周期运动。为了证明这些拟周期运动的存在，接下来利用Runge-Kutta法对离散化模型直接进行相应的数值积分。图6.7（a）给出柔性地基梁当p=0.10时的非周期运动，其中Ω/ω1=1.005。可以看出弹性地基梁跨中位移的时间历程明显呈现出运动的拟周期性。然而，由于高阶项和参数共振项的影响，当激励频率在共振区内缓慢变化时，柔性地基梁并不会发生任何混沌运动。
对于刚性地基梁而言，当激励频率Ω在频率区域Ω/ω1∈（1.32，1.37）缓慢变化时，弹性地基梁似乎经历了以下过程：1T运动→倍周期分岔→2T运动→环面分岔→拟周期运动→折叠分岔→混沌运动→2T运动→倍周期分岔→1T运动。图6.7（b）给出了刚性地基梁当p=0.10时的混沌运动，其中Ω/ω1=1.350。可以看出刚性地基梁的时间历程呈现明显的阵发性，显然这种混沌运动主要由阵发机制激发。
(www.xing528.com)
图6.7 弹性地基梁的非周期运动
（a）柔性地基梁的拟周期运动：Ω/ω1=1.005；（b）刚性地基梁的混沌运动：Ω/ω1=1.350
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
