【摘要】:图6.4刚性地基梁的幅频响应曲线:Ω/ω1≈1.0;Ω/ω1≈2.0 柔性地基梁的幅频响应曲线:Ω/ω1≈1.0;Ω/ω1≈2.0接下来分析大幅激励作用下弹性地基梁的非线性响应,其中激励幅值提高到p=0.20。图6.5给出刚性地基梁与柔性地基梁的最大振幅随激励频率在主共振区和亚谐波共振区中变化情况。从本质上讲,当Ω/ω1≈2.0时,大幅激励影响了弹性地基梁1T运动的稳定性,因此幅频响应曲线存在其他的稳定周期解分支,如图6.5所示。
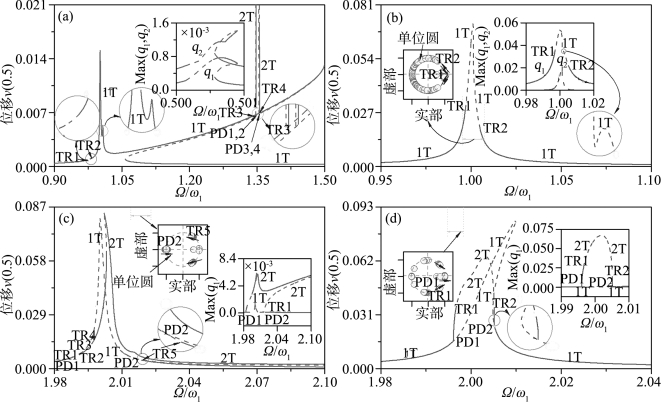
图6.4 刚性地基梁的幅频响应曲线(p=0.10):(a)Ω/ω1≈1.0;(b)Ω/ω1≈2.0
柔性地基梁的幅频响应曲线(p=0.10):(c)Ω/ω1≈1.0;(d)Ω/ω1≈2.0
接下来分析大幅激励作用下弹性地基梁的非线性响应,其中激励幅值提高到p=0.20。图6.5给出刚性地基梁与柔性地基梁的最大振幅随激励频率在主共振区和亚谐波共振区中变化情况。显然,在大幅激励作用下,弹性地基梁响应的非线性效应显著增强,振幅进一步增大。与前面的数值结果相比,幅频响应曲线呈现出定量和定性的差异。从本质上讲,当Ω/ω1≈2.0时,大幅激励影响了弹性地基梁1T运动的稳定性,因此幅频响应曲线存在其他的稳定周期解分支,如图6.5所示。此外,由于参数共振的明显影响,刚性地基梁和柔性地基梁的2T周期解分支存在显著差异。对于前者,1T和2T周期解分支在倍周期性分岔点(PD3和PD4)汇合,并且幅频响应曲线中存在两条不稳定2T周期解分支。对于后者,由于主参数共振引起的参数不稳定性(Ω≈2ω1)出现在Ω/ω1=2.015附近,如图6.5所示,弹性地基梁的幅频响应曲线存在其他2T周期解分支,并且第一阶模态的振幅远大于第二阶模态的振幅。(https://www.xing528.com)
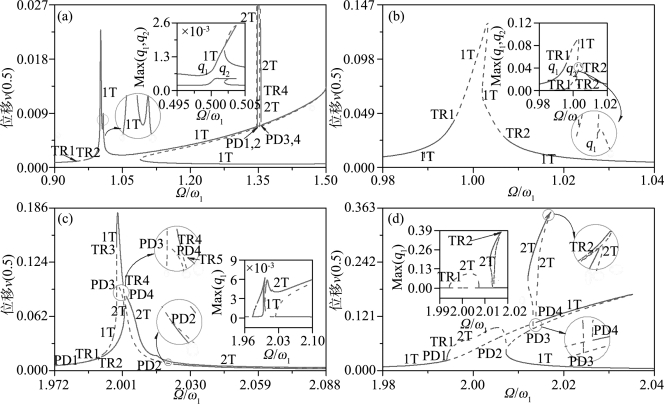
图6.5 刚性地基梁的幅频响应曲线(p=0.20):(a)Ω/ω1≈1.0;(b)Ω/ω1≈2.0
柔性地基梁的幅频响应曲线(p=0.20):(c)Ω/ω1≈1.0;(d)Ω/ω1≈2.0
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




