【摘要】:前面的数值结果主要关注固支-自由梁。实际上,铰支(自由)-自由梁不同固有频率之间同样可能存在2∶1(3∶1)比例关系。当K0=447.11时,铰支-自由梁的前两阶固有频率分别为35.547和71.114。表5.1给出了边界条件对不同弹性地基梁幅频响应曲线分岔点的影响。当Ω≈ω2时,弹性地基梁幅频响应的硬化特性明显增强并且存在较宽的多值区,同时不存在任何两模态响应。然而,当Ω≈ω1时,铰支(自由)-自由梁的幅频响应曲线并不存在任何多值区。
前面的数值结果主要关注固支-自由梁。实际上,铰支(自由)-自由梁不同固有频率之间同样可能存在2∶1(3∶1)比例关系。当K0=447.11(801.62)时,铰支-自由梁的前两阶固有频率分别为35.547(13.324)和71.114(39.934)。当K0=542.45(839.80)时,自由-自由梁的前两阶固有频率分别为40.505(14.678)和81.031(43.996)。显然,这些弹性地基梁的2∶1(3∶1)内共振仍然可能被激发。
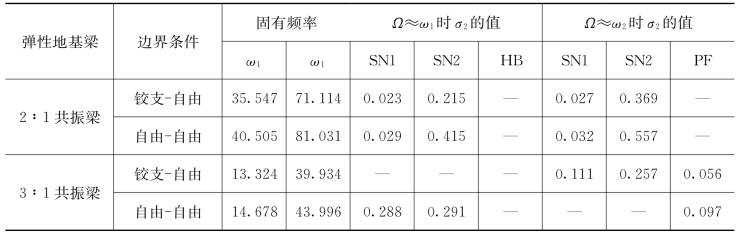
表5.1给出了边界条件对不同弹性地基梁幅频响应曲线分岔点的影响。可以看出,弹性地基梁的单模态响应特性主要由二阶非线性系数Sii控制。当Ω≈ω2时,弹性地基梁幅频响应的硬化特性明显增强并且存在较宽的多值区,同时不存在任何两模态响应。当Ω≈ω1时,系统的非线性响应主要由直接激发模态控制。对于2∶1共振梁而言,铰支(自由)-自由梁的幅频响应并不存在任何Hopf分岔和叉形分岔。相反,3∶1共振梁的幅频响应曲线只存在叉形分岔,因此相应的弹性地基梁可能存在两模态解。然而,当Ω≈ω1时,铰支(自由)-自由梁的幅频响应曲线并不存在任何多值区。(https://www.xing528.com)
表5.1 边界条件对弹性地基梁幅频响应曲线分岔点的影响
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




