剪力地基动能分析：精细化动力设计

第2章建立的理论模型假定弹性地基梁轴向不承受荷载，且符合不可伸长条件。显然，基本可忽略弹性地基梁的轴向力F1。因此剪力F2主导了弹性地基梁的动力设计：F2=j¨v′-EIv‴-h（k0v-k1v″+Pcosωt）v′/2。图5.18（a）和（b）给出了弹性地基梁剪力随时间的变化。可以看出，弹性地基梁上剪力最大值主要发生在梁的左端（固支端）。而且间接激发模态对弹性地基梁的剪力响应有明显的影响。需要指出的是，与单模态结果相比，双模态解确定的剪力在Ω≈ω1时沿梁长方向有明显的波动。

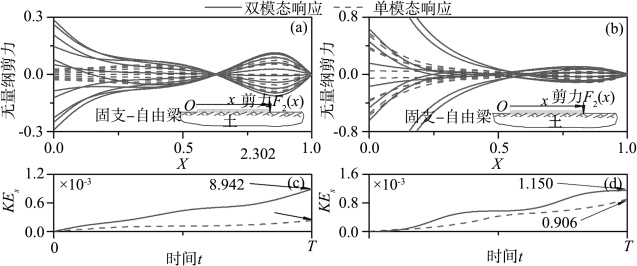
图5.18　弹性地基梁的剪力

（a）2∶1内共振；（b）3∶1内共振；动能：（c）2∶1内共振；（d）3∶1内共振(www.xing528.com)

另一方面，为了更好地研究土-结构相互作用问题，需要考虑土-结构相互作用激发的土场能量传输。如果已知弹性地基的基本参数（杨氏模量Es和泊松比νs），那么可以确定出弹性地基所吸收的能量。从物理层面而言，地基所吸收的能量主要由梁的振动通过地基反力传输到土场中。确定出该能量后，就可以粗略估算出整个运动过程中地基吸收的能量。总体而言，地基吸收的无量纲能量KEs可以表示为：

图5.18（c）和（d）分别给出了一个周期内地基吸收能量变化情况。显然，地基吸收的能量随时间增长而单调增大。另一方面，单模态响应明显低估了弹性地基所吸收的能量，从而导致低估土场波动情况。从这个角度而言，弹性地基梁的内共振显著增加了振动过程中弹性地基吸收的能量。