对于第二阶模态主共振情况（Ω≈ω2），弹性地基梁平均方程的极坐标形式可以表示成：
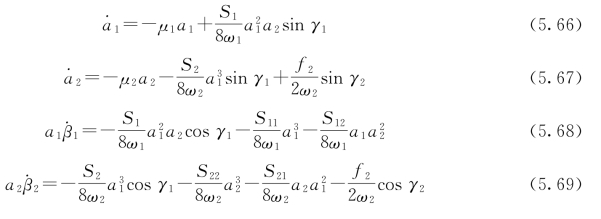
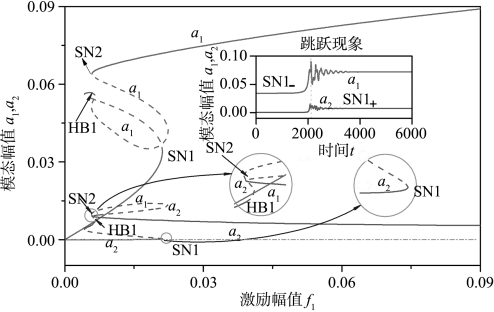
图5.12 弹性地基梁的激励响应曲线（σ2=0.04和Ω≈ω1）
相应的间接激发模态幅值为：a1=（-S1cosγ2±Δ）/2S11。
图5.13给出了第二阶模态主共振时（Ω≈ω2）弹性地基梁第一阶模态和第二阶模态的幅频响应曲线，其中f2=0.01。可以看出弹性地基梁的单模态响应呈明显的硬化行为。同时，幅频响应曲线在较宽的频率区域内存在两模态解。对于两模态解分支而言，稳定的平衡解在HB1处经过Hopf分岔失去其稳定性，同时不稳定解分支也在HB1处存在Hopf分岔。值得指出的是，间接激发的低阶模态幅值远大于高阶模态幅值。因此，高阶模态主导了弹性地基梁的非线性响应。
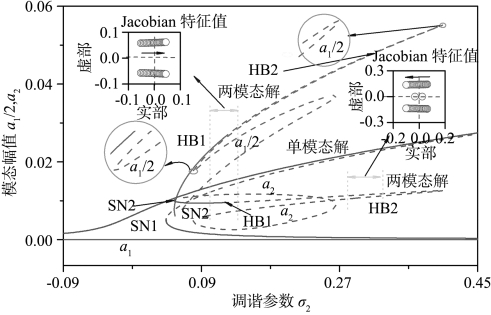
图5.13 弹性地基梁的幅频响应曲线（f2=0.01和Ω≈ω2）
图5.14给出了平均方程的周期解分支，其中TR为环面分岔点。可以看出，随着调谐参数σ2的减小，非稳定极限环单调增大。另外，非稳定周期解分支在PD1处存在倍周期分岔。此外，还可以看出，不稳定周期解经历了一系列倍周期分岔，并在PD2处获得其稳定性。然而平均方程稳定周期解仅存在于一个特定的频率区间，并且在TR1处经过环面分岔失去其稳定性。
(www.xing528.com)
图5.14 弹性地基梁平均方程的周期解分支（f2=0.01和Ω≈ω2）
图5.15给出了弹性地基梁平均方程的数值积分结果，其中σ2=0.154。可以看出动态解的拟周期性。然而，随调谐参数σ2的减小，平均方程并不会出现混沌解。相反，由于初值条件的变化，拟周期解会跳跃到两模态解或者单模态解。值得注意的是，如果外激励幅值f2轻微增大，如f2＞0.0105，那么平均方程的动态解将进入混沌区。图5.16给出了弹性地基梁平均方程的混沌解，其中f2=0.011。对比图5.15可以看出，平均方程经历了环面的破坏。
图5.15 弹性地基梁的平均方程的拟周期解
（a）时间历程；（b）FFT；（c）庞加莱截面
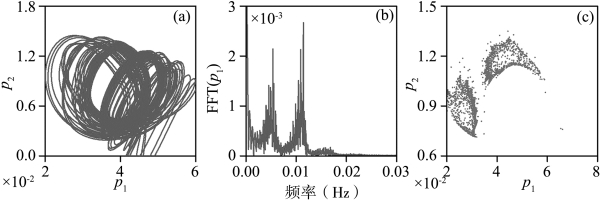
图5.16 弹性地基梁的平均方程的混沌解
（a）相图；（b）FFT；（c）庞加莱截面
图5.17给出了弹性地基梁的激励响应曲线，其中σ2=0.10。可以看出，两模态解在整个区域内基本一直存在，而且弹性地基梁间接激发模态的幅值明显大于直接激发模态的幅值。
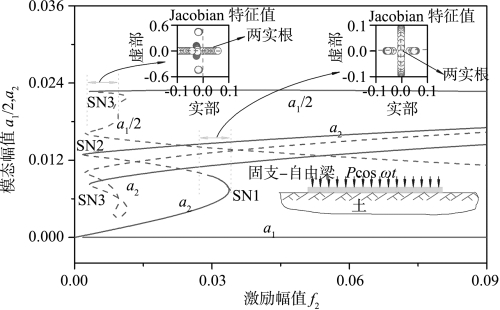
图5.17 弹性地基梁的激励响应曲线（σ2=0.10和Ω≈ω2）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
