对于第二阶模态主共振情况(Ω≈ω2),弹性地基梁平均方程的极坐标形式可以写成:

图5.4给出了第二阶模态主共振时(Ω≈ω2)弹性地基梁第一阶模态和第二阶模态的幅频响应曲线,其中f2=0.002,PE为叉形分岔点。可以看出,单模态解并不存在任何多值区域,并且通过在PE1处的叉形分岔从而失去其稳定性,相反通过PE2处的另一叉形分岔又重新获得其稳定性。另一方面,两模态解存在两个明显的多值区。在左边的多值区内,弹性地基梁的非线性响应主要由直接激发模态控制。然而,在右边的多值区内,弹性地基梁的非线性响应由间接激发模态控制,而且两模态解分支存在两个Hopf分岔点。
在两个Hopf分岔点之间(HB1和HB2),弹性地基梁的平均方程可能呈现出丰富的非线性动力学现象。图5.5给出了相应的周期解分支变化情况,其中CE为折叠分岔。可以看出,从HB1和HB2处衍生的周期解分别通过不同的倍周期分岔从而失去其稳定性(PD1和PD3)。随着调谐参数σ2的减小,后者通过在PD4处的倍周期分岔获得其稳定性,并且在CE1处存在一个折叠分岔。同时可以看出,从CE1处开始的周期解分支逐渐接近鞍点。图5.6给出了周期解的周期T随调谐参数σ2的变化情况。可以看出系统存在相应的同宿轨道[53],如图5.5所示。相反,从PD1和PD3处衍生的P-2周期解经过一系列倍周期分岔从而导致混沌,如图5.7(a),(c)所示。然而,随调谐参数σ2的进一步增大或减小,将会出现两种不同的激变现象:P-1周期解和更大的混沌吸引子,如图5.7(b)所示。值得指出的是,该混沌吸引子经历一系列反向倍周期分岔后,从而导致P-1周期解。
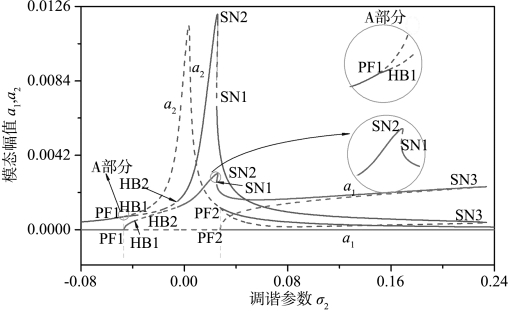
图5.4 弹性地基梁的幅频响应曲线(f2=0.002和Ω≈ω2)
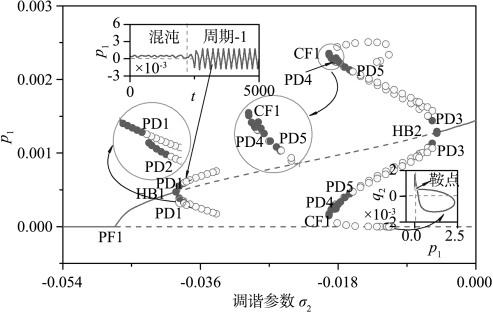
图5.5 弹性地基梁平均方程的周期解分支(σ2∈(-0.0391,-0.0042))(https://www.xing528.com)
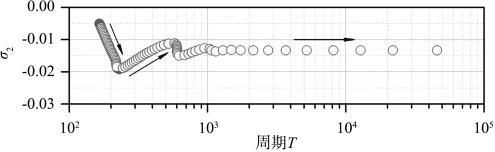
图5.6 弹性地基梁平均方程周期解的周期T:Ω≈ω2。
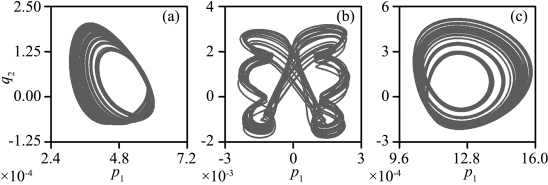
图5.7 弹性地基梁平均方程的混沌吸引子
(a)σ2=-0.0382;(b)σ2=-0.0073;(c)σ2=-0.0065
图5.8给出弹性地基梁的激励响应曲线,其中调谐参数σ2=0.04。可以看出,单模态解通过在PE1处的亚临界叉形分岔失去其稳定性。同时,相应的叉形分岔导致了系统两模态解的出现,而且该单模态解通过在SN1处的鞍结分岔重新获得其稳定性。当外激励幅值f2从SN3处增大时,第一阶模态的幅值出现明显的饱和现象。同时,间接激发模态对弹性地基梁非线性响应的影响相对较小。
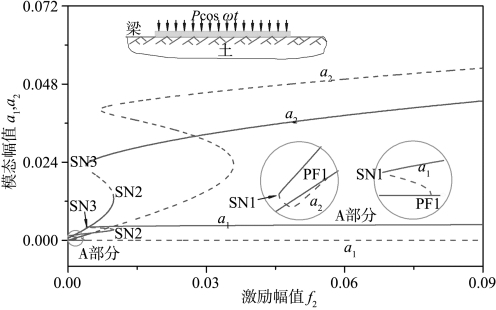
图5.8 弹性地基梁的激励响应曲线(σ2=0.04,Ω≈ω2)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




