超谐波共振响应及其应用-土结构相互作用中的精细化动力学

对于2次超谐波共振情况（Ω≈ωn/2），引入调谐参数σ，使其满足：2Ω=ωn+ε2σ，并将外激励幅值p调整为ε3/2p。因此激励项出现在ε3/2阶：

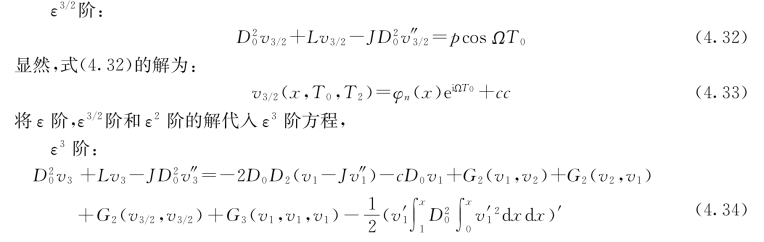
可以得到2次超谐波共振（Ω≈ωn/2）的可解性条件为：

相应地，弹性地基梁2次超谐共振位移v（x，t）二阶近似表达式可以写成：

对于3次超谐共振情况（Ω≈ωn/3），引入调谐参数σ，使其满足：3Ω=ωn+ε2σ。调整外激励项p为εp。利用多尺度法所得到的各阶方程与1/3次亚谐共振情况一致。因此，可解性条件可以写成[47]：(www.xing528.com)

图4.3　弹性地基梁超谐波共振幅频响应曲线

（a）2次超谐共振（Ω≈ωn/2）；（b）3次超谐共振（Ω≈ωn/3）

图4.3（a）给出了弹性地基梁2次超谐共振时的幅频响应曲线（Ω≈ωn/2），其中激励幅值p=3.2。可以看出，随着Winkler参数K0的增大，弹性地基梁的非线性响应幅值明显减小。相反，非线性软化特性增强，从而导致更宽的多值区。

图4.3（b）给出了弹性地基梁3次超谐共振时的幅频响应曲线（Ω≈ωn/3），其中激励幅值p=6.4。可以看出，不同Winkler参数K0导致不同的初始偏移量。随Winkler参数K0的增大，骨架曲线的初始偏移量有一定的右移。同时，非线性响应的幅值也明显减小。值得指出的是，当Winkler参数K0=500时，弹性地基梁的非线性特性并不明显。