在这一节里，主要研究弹性地基梁的非线性模态和非线性频率。理论上讲，可以通过不同的方法确定连续系统的非线性模态。然而目前的理论模型考虑了二次弯矩效应，弹性地基梁的保守特性被破坏。因此，可以利用多尺度法[43]确定弹性地基梁的非线性模态。按照这种方法，弹性地基梁的位移v（x，t）可以表示为：
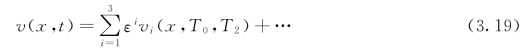
其中，ε为小参数（ε≪1）；Ti=εit（i=0，2）。显然∂/∂t=D0+ε2D2+…。将式（3.19）代入式（3.1），并按小参数ε的幂次进行整理，可以得到：
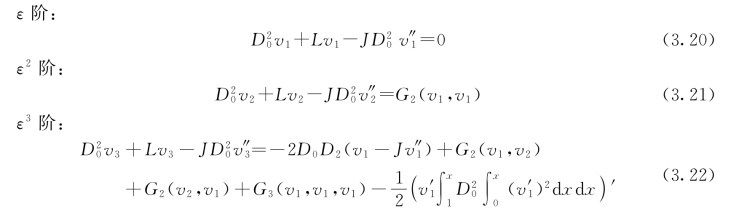
其中忽略了式（3.22）中的激励项和阻尼项。对于第n阶模态非线性自由振动，式（3.20）的解可以写成：
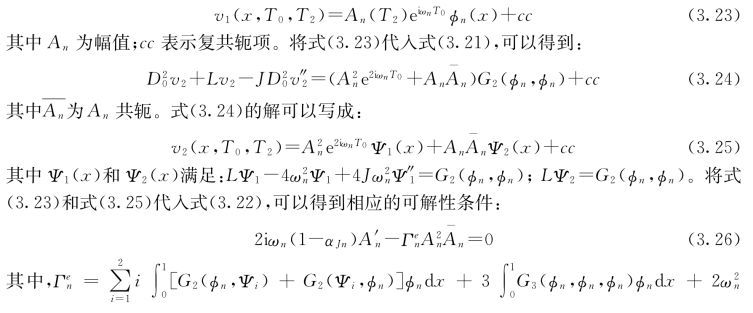
其中，已令小参数ε=1；βn0为常数；ωNn为非线性固有频率
可以看出式（3.29）中包含与时间t无关的漂移项
显然，弹性地基梁非线性响应并不同步。因此与Rosenberg定义的非线性模态概念相比，目前的非线性模态存在本质的差别。另外，如果非线性系数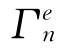
已知，则非线性频率ωNn主要由响应幅值an确定。
图3.5给出了弹性地基梁的非线性频率与非线性响应幅值之间的关系，可以看出相应的骨架曲线呈硬弹簧特性，而且硬弹簧特性随着Winkler参数K0的增大而增强。相反，剪切参数K1对非线性响应起软化作用。为进一步研究弹性地基参数对骨架曲线的影响，图3.5中还对比了截止频率前后骨架曲线的差别。对比K0=500，可以看出当K0=700时的骨架曲线呈现出更强的硬弹簧特性。显然，弹性地基梁的边界条件明显影响骨架曲线的非线性特性。值得指出的是，随着边界约束的放松，弹性地基梁非线性响应的硬化特性进一步增强。(www.xing528.com)
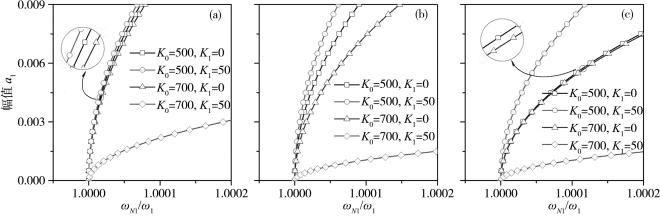
图3.5 弹性地基梁第一阶固有模态的非线性频率
（a）固支-自由梁；（b）铰支-自由梁；（c）自由-自由梁
此外，利用式（3.29）可以确定不同时刻下的弹性地基梁非线性动力构型。图3.6给出了弹性地基梁零速度模态及其在非线性半周期TN1内的演化过程。可以看出，当K0=500时，第一阶和第二阶非线性模态之间的差别相对较小。而且，截止频率明显影响二阶非线性模态。当K0=700时，弹性地基梁的非线性模态存在定量的差别。另外，随边界约束放松，这种非线性模态之间的差别明显减小。
另一方面，由图3.6（c）可知，自由-自由梁的左端存在明显的非零竖向位移v。因此，弹性地基梁存在小的轴向位移u。值得注意的是，在建立弹性地基梁的非线性运动方程（式（3.1））时考虑了弹性地基梁轴向位移u的影响，并且利用了边界条件：u|x=0=0。然而这种边界条件对于自由-自由梁而言并不成立（见图3.6（c））。显然，这种不同会导致自由-自由梁的非线性模态发生小的变化。当然，如果弹性地基梁足够长，那么可以忽略这种较小的差别。
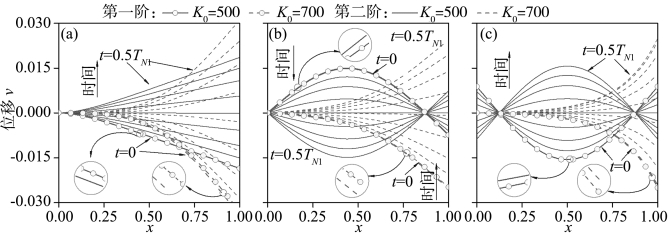
图3.6 弹性地基梁在K1=50和a1=0.01时的零速度模态构型（粗线）及其非线性半周期TN1内的演化过程
（a）固支-自由梁；（b）铰支-自由梁；（c）自由-自由梁
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
