建模理论实践，固支-自由梁分析与动力设计

对于固支-自由梁，边界条件可以写为：

利用上面的边界条件，可以确定相应的特征值问题。然后基于该问题的特征值分析可以得到固支-自由梁的频率方程：

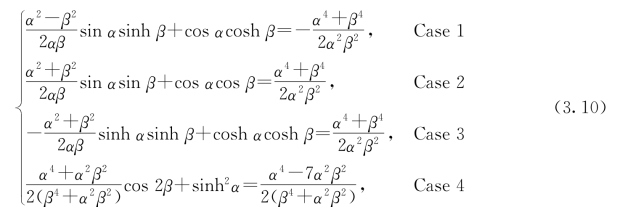
利用式（3.10）可以确定弹性地基梁的第i阶固有频率ωi。在此基础之上，可以确定系数αi和βi。相应的弹性地基梁第i阶固有模态φi（x）可以表示为：(www.xing528.com)

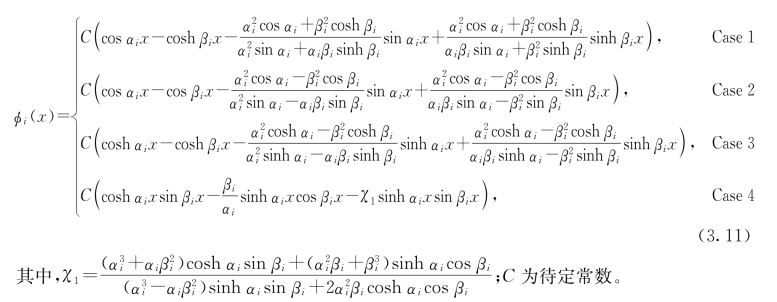
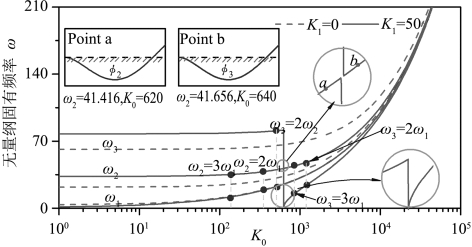
图3.1　弹性地基Winkler参数K0对固支-自由梁固有频率的影响

考虑弹性地基梁的材料特性参数：长度为l=6.096 m，高度为h=0.305 m，宽度为b=0.61 m，密度为ρ=2.403×103kg/m3，弹性模量为E=2.482×104MPa。图3.1给出了弹性地基Winkler参数K0对固支-自由梁固有频率的影响。可以看出，当弹性地基为Winkler模型时，固有频率随Winkler参数K0的增大而增大。同时剪切参数K1也明显影响地基梁的固有频率。实际上，剪切参数K1的引入减小了第一阶固有频率。值得注意的是，在K1=50且K0=625时，固有频率谱中存在截止频率（cut-off frequency），从而导致了相应的跳跃现象。当K0≈625时，截止频率导致弹性地基梁的相邻两阶固有频率迅速接近并分离，因此弹性地基梁的频谱上存在明显的频率偏转现象（curve-veering phenomenon）。