【摘要】：根据Newton法，可以得到弹性地基梁在x轴和y轴方向力的平衡方程：其中，mb=ρbAb为梁的单位长质量；ρb为梁的密度；Ab=bh为梁的横截面积；F1和F2分别为轴向力和剪力；p（x，t）为外荷载。如图2.2所示，弹性地基上梁的弯矩平衡公式可以表示为：其中，j≡为转动惯量；Mb为梁单元的弯矩。式左侧第三项为外荷载和地基反力沿ξ轴方向的分量导致的二次弯矩项；式右端项为转动惯量引起的弯矩。与此同时，弹性地基梁的边界条件为：
根据Newton法，可以得到弹性地基梁在x轴和y轴方向力的平衡方程：
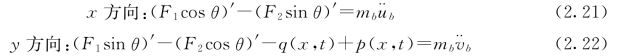
其中，mb=ρbAb为梁的单位长质量；ρb为梁的密度；Ab=bh为梁的横截面积；F1和F2分别为轴向力和剪力；p（x，t）为外荷载。如图2.2所示，弹性地基上梁的弯矩平衡公式可以表示为：
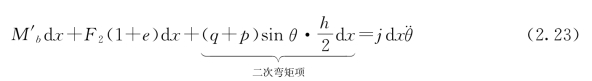
其中，j≡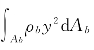
为转动惯量；Mb为梁单元的弯矩。式（2.23）左侧第三项为外荷载和地基反力沿ξ轴方向的分量导致的二次弯矩项（见图2.2）；式（2.23）右端项为转动惯量引起的弯矩。利用该式，可以得到剪力F2的表达式：
若假设弹性地基梁的中轴线与x轴重合，则弯矩Mb可以表示为：(www.xing528.com)
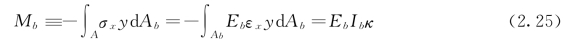
其中，Ib=
为梁的截面惯性矩。将式（2.19）代入式（2.21），并在x∈（x，L）内积分；另一方面利用不可伸长边界条件Fx|x=L=0，可以得到轴向力F1的表达式：
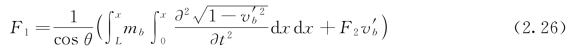
将式（2.24）和式（2.26）代入式（2.22），并利用式（2.19）、式（2.20）和式（2.25）及地基反力的统一公式（2.7），可以得到弹性地基梁的非线性面内运动方程[39]：
上式只保留到三次非线性项，并引入了阻尼项
（cb为黏滞阻尼系数）。与此同时，弹性地基梁的边界条件为（x=0，L）：
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
