汽车维修钣金工-平面弯曲和纯弯曲

当直杆受到垂直于轴线的外力作用时，其轴线由直线变为曲线，这种变形称为弯曲变形。发生弯曲或弯曲变形为主的杆件称为梁。梁的横截面具有对称轴线和对称平面。

如果梁上的外力或力偶都位于对称平面内，且外力垂直于轴线，则变形后的轴线将是平面曲线，并仍位于对称平面内，这种情况称为平面弯曲。平面弯曲是最普通，也是最常见的弯曲形式。

1.力和弯矩的概念

在图6-12中，当梁N_A—N_B受到载荷F的作用时，如果梁在发生微量变形后进入平衡状态，这时，梁上的受力状况是一个平衡力系的状态。根据受力状态分析可知梁主要受到剪力和弯矩作用。从Q到Q′平面来看，处于N_A到Q的一段必然有应力向上；处于N_B到Q的一段有向下应力，因此Q到Q′平面上产生剪应力。

N_A到F是一个力偶现象，N_B到F也是一力偶现象。

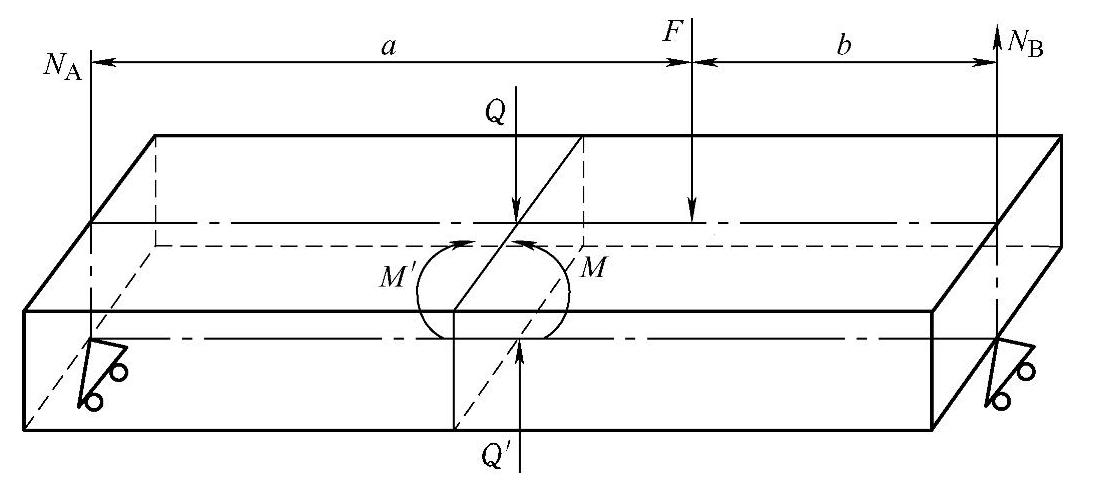
图6-12 力和弯矩的概念

N_A到F受到弯曲力其力臂为a，弯矩力Fa。

N_B到F受到弯曲力其力臂为b，弯矩力Fb。

由以上分析可以得到以下结论：切于QQ′横截面的力称为剪力，剪力的作用线通过截面形心，与外力平行。力偶矩M和M′称为弯矩，弯矩是力偶面与横截面垂直的内力。

2.纯弯曲梁横截面上的应力

在一般情况下，梁的弯曲横截面上既有剪应力，又有弯矩力，剪应力的存在说明梁不仅有弯曲变形，且有剪切变形，这种平面弯曲称为剪切弯曲。

如果各横截面上，只有弯矩，而无剪力，则称为纯弯曲。如图6-13所示，F—A和B—F，属于剪切弯曲。A—B属于纯弯曲。纯弯曲的梁横截面上没有剪应力，只有弯矩力。

3.中性层的概念

如果我们将梁看成是由无数纵向纤维组成的，假设所有纤维只受纵向的拉伸和压缩时，互相无挤压，那么梁在弯曲时，必然以形心形成中性层，在弯曲突起的中性层以上，纵向纤维受拉伸作用；中性层以下，纵向纤维受压缩作用，如图6-14所示。

图6-13 A—B属于纯弯曲

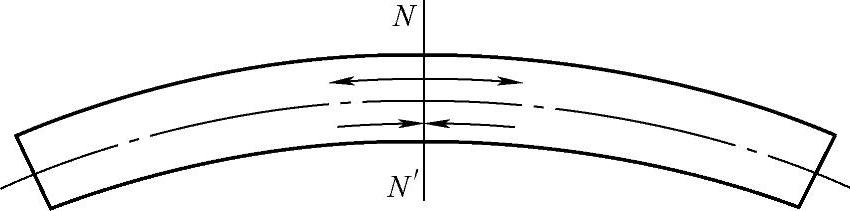
图6-14 中性层的概念

其应力状态是中性层的纵向平面内应力为零，中性层以上是拉伸应力，中性层以下是压缩应力，应力的大小与其离中性轴的距离成正比。Y值相同的点应力值相同，如图6-15所示。

当截面形状对称于中性轴时，如矩形、圆形、工字形等，最大拉应力等于最大压应力。

当截面形状不对称中性轴时，如T字形（见图6-16）、槽型等截面，拉应力和压应力的最大值就不相等。

图6-15 对称截面应力分布

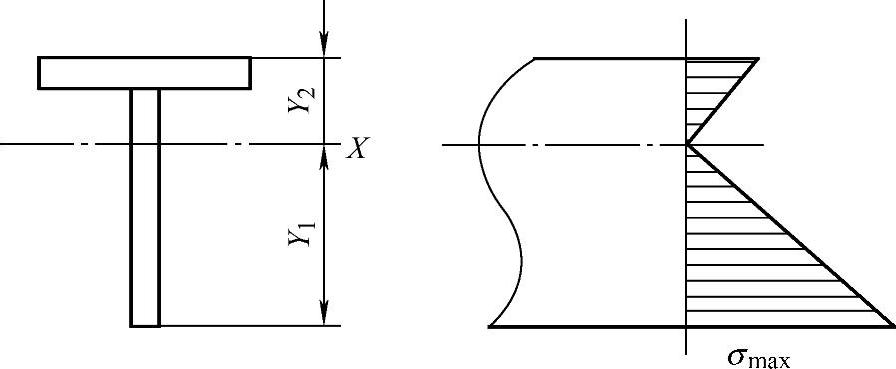
图6-16 T字形截面应力分布(www.xing528.com)

因此，在设计框架结构上应用到截面形状不对称中性轴的材料时，就应该将应力大的一面放在受压应力的方向上比放在受拉的应力方向上更为经济和可靠一些，因为，材料在受压时比受拉时更不易损坏。

4.梁的剪应力概念

剪切弯曲时，梁的横截面上有剪应力，相应地在纵截面也上有剪应力，根据剪应力互生定律（受力物体内，某一点处所做的两个互相垂直的截面上的剪应力，必定是成对存在，且数值相等，同时都垂直于两个截面的交线方向，则共同指向或背离这一交线）梁的纵向截面也相应地有剪应力。比如：竹竿在弯曲时常出现沿纵向开裂，说明梁在弯曲时纵向剪应力的存在，而竹竿沿纵向的剪力强度较弱，因而沿纵向被剪坏。

剪应力在横截面上的分布规律与截面的形状有一定关系。一般情况下，其大小沿截面高度方向呈曲线变化，且中性轴上各点的剪应力最大，如图6-17所示。横截面上各点的剪应力平行于剪力面，中心轴距离相同的各点剪应力大小相等。

图6-17 中性轴上各点的剪应力最大

横截面上各点的剪应力平行于剪力面，中心轴距离相同的各点剪应力大小相等

5.典型梁的受力分析

（1）悬臂梁在集中力作用下的受力情况 如图6-18所示为台钻的手柄，其在集中载荷作用下的受力分析如下：

因为F=Q，其中Q=剪力，根据剪应力互生定律，所以各横截面上剪切力均等于F。

因为M=FL，当F在0位时，弯矩M=FL=0；当F在L段时，则FL=M。因此，悬臂梁的固定端横截面上的弯矩力最大。

（2）简支梁在均布载荷作用下的受力情况 如图6-19所示为简支梁在均布载荷作用下的剪力和弯矩变化规律。

6.提高梁弯曲强度的措施

（1）降低最大弯矩值M_max 最大弯矩值不仅决定于力的大小，而且决定于力在梁上的分布，力的大小是由工作需要而定，而力在梁上的分布合理性，可以通过支座和载荷的合理布置达到。

例如：承受均布载荷的简支梁，最大弯矩值为FL²/8，若把两端支座各向里移动L/5。则最大弯矩为0.025FL²，仅为前者的1/5，故而在同样的载荷下，梁的截面可以减小，这样就大大节省了材料，并减轻自重，如图6-20所示。

图6-18 台钻的手柄的剪力图和弯矩图分析

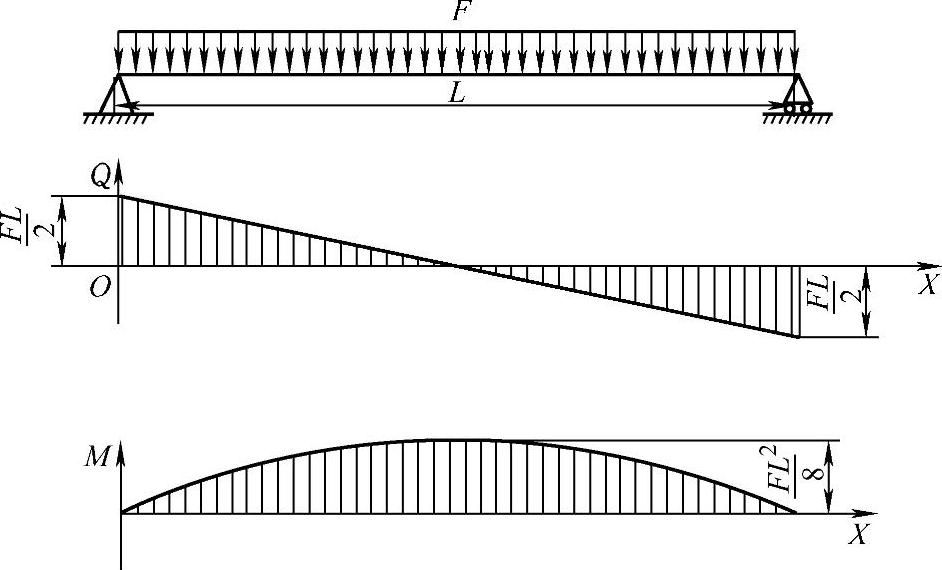
图6-19 简支梁在均布载荷作用下的剪力和弯矩变化规律

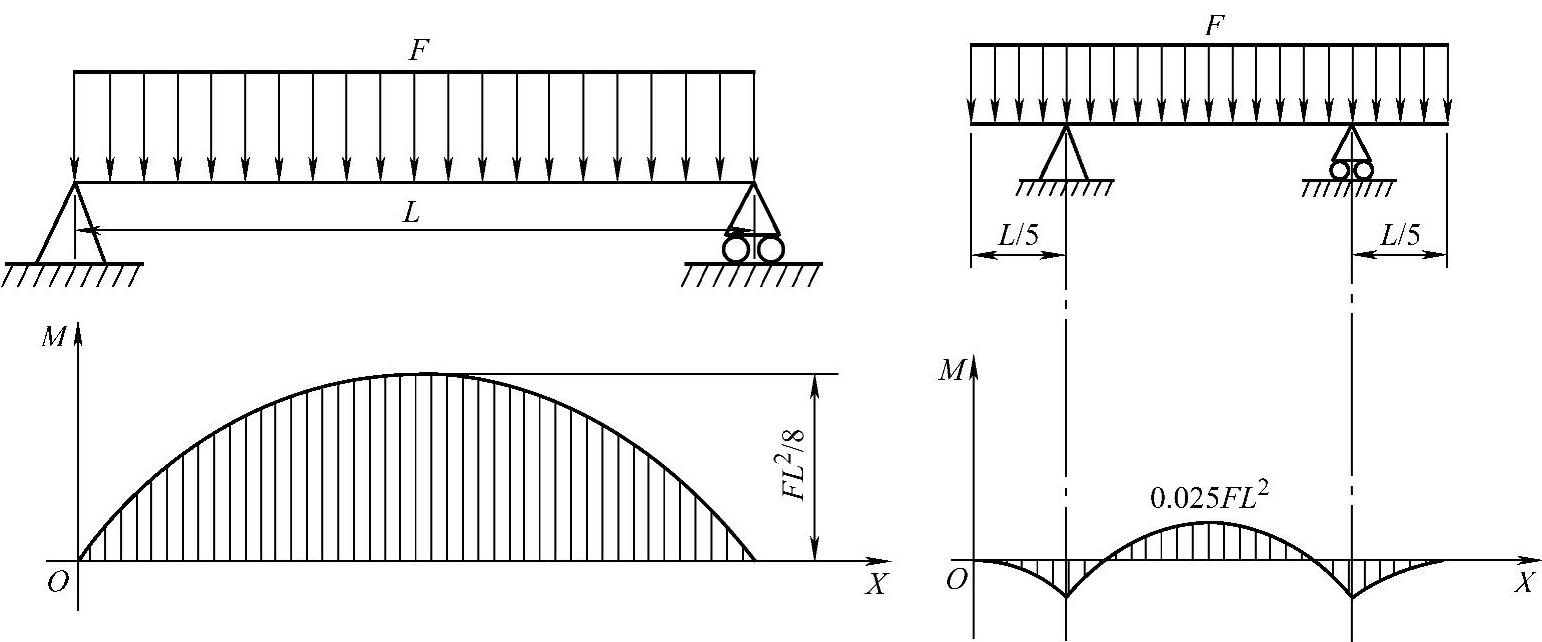
图6-20 支座位置与最大弯矩的关系

（2）选择合理的截面形状

1）选择抗弯截面模量与截面面积的比值高的截面。因为抗弯截面模量是控制弯曲强度的另一个重要因素。它的大小不仅和截面面积有关，而且与截面形状有关，用料的多少只决定于截面的面积，比值越大，说明在相同截面面积的条件下，抗弯截面模量越大，也就是在相同的用料条件下，梁的承载能力高，所以比值大的截面合理。

2）根据材料的特性选择截面。当材料的拉压强度相等时，要求截面形状应对称于中心轴，采用矩形、工字形等截面形状为合理。当材料的拉压强度不等时，则要求截面形状不对称于中性轴，采用T字形、槽型等截面形状较为合理。

3）从等强度角度确定截面尺寸。等截面梁的截面尺寸是由最大弯矩确定的，其他截面由于弯矩小，最大应力都未达到许用值，材料未得到充分利用。因此，从整体来说，等截面梁是不合理的。故工程中常出现变截面梁。如：摇臂钻床的横臂、汽车上的板簧、阶梯轴等。它们的截面尺寸都随弯矩大小而变，若各截面的最大应力都达到许用值，因此称为等强度梁。