1.等长桩
群桩的水平位移用表示群桩相对水平位移的群桩水平位移折减系数RRρ表示[Poulos(1971b)]

在两种水平荷载和桩顶自由条件下,用RRρH和RRρM分别表示仅受水平力和仅受弯矩的桩顶自由桩的群桩位移折减系数;同理,用RRθH和RRθM分别表示仅受水平力和仅受弯矩的桩顶自由桩的群桩转角折减系数。在桩顶固定条件下,用RRρF表示仅受水平力的桩顶固定桩的群桩位移折减系数。
为了进一步验证本书在考虑桩的存在对地基土变形带来影响的有效性,即克服现有方法忽略群桩“加筋效应”的可行性,将本书方法与Poulos(1971b)的弹性理论计算结果进行了比较。在图5.13 中,土的泊松比μs= 0.5,桩长细比L/d = 25,桩的柔度系数KR=EpIp/EsL4= 10-5。对于桩顶固定时3 ×3 桩群桩和桩顶固定时4 ×4 桩群桩,当桩间距s/d = 2时,本书方法所求得的群桩折减系数比Poulos(1971b)的解答小27%。

图5.13 不同群桩的群桩折减系数的影响对比(L/d=25,KR=10 -5)
在图5.14 中,土的泊松比μs= 0.5,桩长细比L/d = 25,桩的柔度系数KR= EpIp/EsL4=10-5、10-1。对于桩顶固定时3 ×3 桩群桩和桩顶固定时4 ×4 桩群桩,桩间距s/d =2 时,当KR= 10-1时,即桩身刚度较大时,两种方法的计算结果相差不大,即Poulos(1971b)方法所求得的群桩折减系数比本书的解答大6%;但当KR= 10-5时,即桩身刚度较小时,Poulos(1971b)方法所求得的群桩折减系数比本书解答大27%。
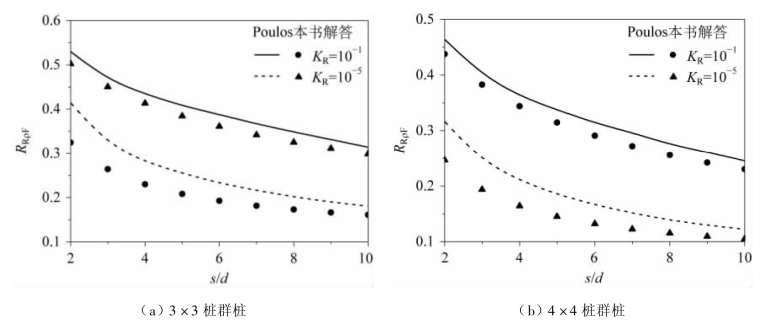
图5.14 不同刚度群桩折减系数的影响对比(L/d=25)
在图5.15 中,土的泊松比μs= 0.5,桩长细比L/d = 10 和100,桩的柔度系数KR=EpIp/EsL4= 10-5。对于桩顶固定时3 ×3 桩群桩和桩顶固定时4 ×4 桩群桩,当L/d = 100 时,桩间距s/d = 2 时,两种方法的计算结果相差不大,即Poulos(1971b)方法所求得的群桩折减系数比本书的解答大17%;但对于L/d =10 时,即桩长较小时,Poulos(1971b)方法所求得的群桩折减系数比本书的解答大60%。
 (https://www.xing528.com)
(https://www.xing528.com)
图5.15 不同桩长群桩折减系数的影响对比(KR=10 -5)
在图5.16 中,土的泊松比μs= 0.5,桩长细比L/d = 25,桩的柔度系数KR= EpIp/EsL4=10-5。对于3 ×3 桩桩顶自由群桩和4 ×4 桩桩顶自由群桩,桩间距s/d = 2 时,Poulos(1971b)方法所求得的群桩折减系数比本书的解答大24%和28%。

图5.16 桩顶自由桩的群桩折减系数的影响对比(L/d=25,KR=10 -5)
从上面的比较结果可以看出,本书计算结果相对于Poulos(1971b)的解答要小。这是由于Poulos 的群桩计算方法,忽略了群桩在土中的“加筋效应”,没有考虑邻桩的存在对土的变形的影响,即过高估计了群桩中桩—桩之间的相互作用,从而使计算的群桩的沉降偏大。本书方法能够考虑桩对土的“加筋效应”,可以更加准确地计算桩—桩之间的相互作用,本书方法显然更可行。
2.非等长桩情况
根据式(5.21)对等长桩群桩的折减系数的定义,非等长群桩的折减系数表示为

该式也可以用来表达不同刚度、不同直径等各种混合桩型群桩的折减系数。
为了验证本书非等长桩群桩桩顶固定时群桩折减系数计算结果的正确性,与等长桩解法进行了比较。即长桩和短桩的桩长细比都为L/d = 50,土的泊松比μs= 0.3,桩土弹性模量比为Ep/Es= 1 000。从图5.17 可以看出两种解法计算结果完全一致。

图5.17 桩顶固定时的非等长桩群桩折减系数对比
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




