桩顶固定位移相互作用系数的变化

1.与Poulos（1971b）解答的对比

为了说明本书计算结果与Poulos（1971b）解答的区别，取土的泊松比μs= 0.5，不同的桩长细比L/d = 10、25，不同的水平荷载作用方向线偏离角β = 0°、90°，不同的桩身刚度系数KR= EpIp/EsL4= 0.001、0.1、10 情况下两根桩顶固定桩的位移相互作用系数进行比较。

从图3.9 ～图3.11 可以看出，对于两种水平荷载作用方向线偏离角，当桩身刚度系数较大时（KR= 10），两种计算方的计算结果相差较小，而当桩身刚度系数较小时（KR= 0.001），本书计算结果都比Poulos（1971b）的解答小。所得出的比较结论与桩顶自由时的相同，这是由于本书在计算两根桩之间的相互作用系数时，考虑了桩在土中的“加筋效应”。

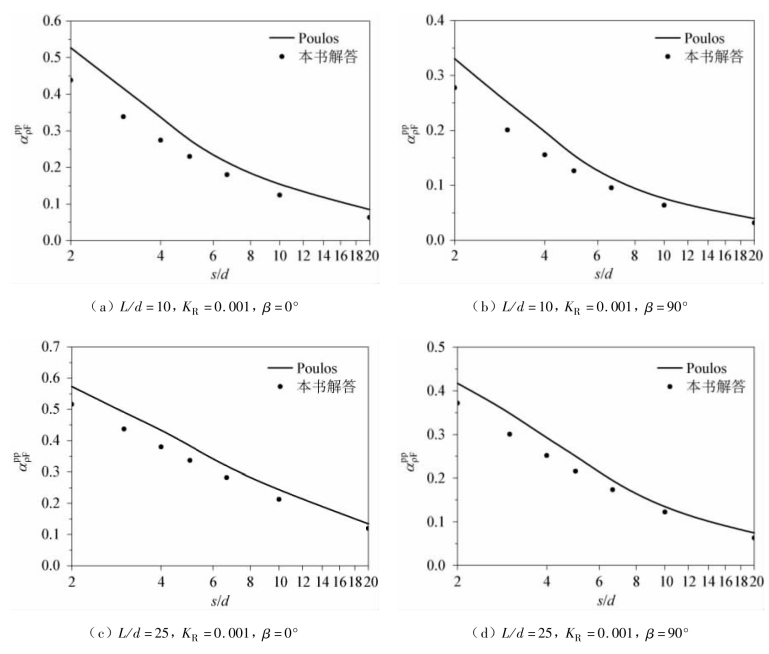
图3.9　桩顶固定的位移相互作用系数随桩距的变化

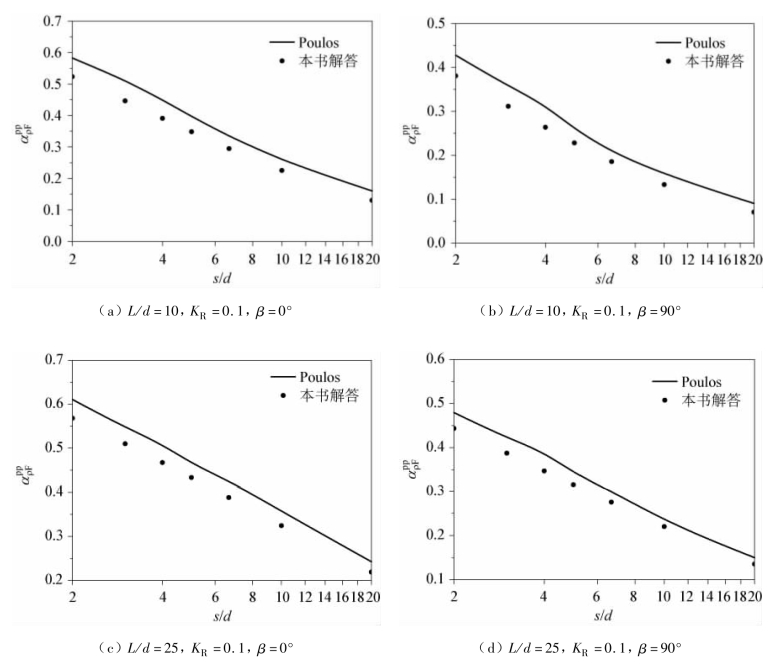
图3.10　桩顶固定的位移相互作用系数随桩距的变化

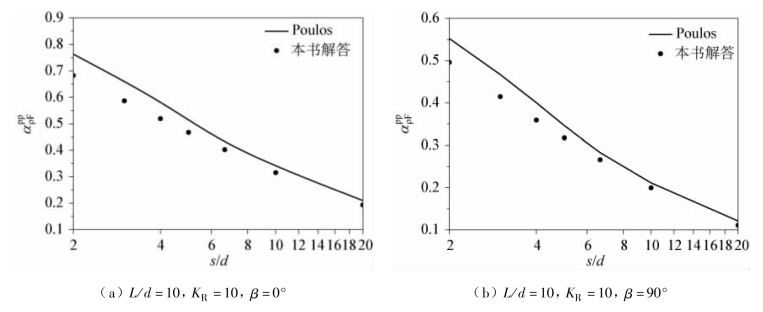
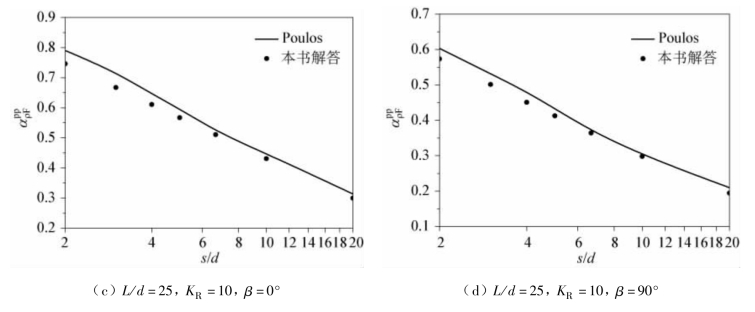
图3.11　桩顶固定的位移相互作用系数随桩距的变化

2.与Leung 等（1987）、Randolph（1981）和Poulos（1971b）解答的对比

为了说明本书计算结果与其他学者解答的区别，图3.12 给出了与Poulos（1971b）、Randolph（1981）和Leung 等（1987）解答的对比结果。土的泊松比μs= 0.5，刚度系数KR=EpIp/EsL4= 10-5，桩长细比L/d = 25。除了当荷载作用方向线偏离角β = 90° 和桩心距s/d = 2 以外，对于其他的不同桩心距，Leung 等（1987）、Randolph（1981）的计算结果相差不大，本书计算结果比两者的计算结果相略小，而Poulos（1971）的计算结果偏大。(www.xing528.com)

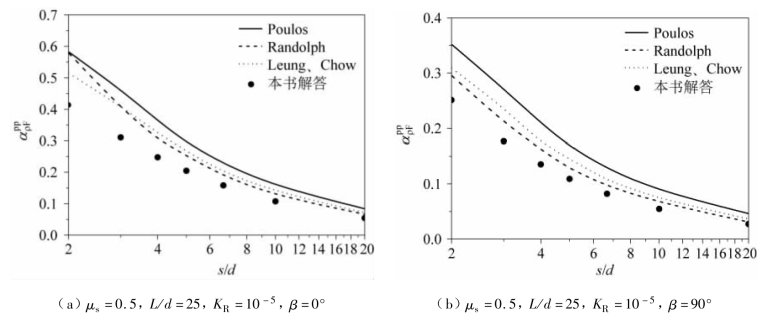
图3.12　仅受水平力作用下两桩相互作用系数的比较

3.与El Sharnouby 等（1985）和Poulos（1971b）解答的对比

图3.13 给出了与El Sharnouby 等（1985）和Poulos（1971b）解答的对比结果。土的泊松比μs= 0.5，不同的刚度系数KR= EpIp/EsL4= 10-5、10-3，桩长细比L/d = 25。与桩顶自由桩比较结果类似，对于柔性桩，Poulos（1971b）的计算结果比El Sharnouby 等（1985）的计算结果大20%，但当El Sharnouby 等（1985）采用与Poulos（1971b）相同的计算单元数时，两种计算方法的结果接近［El Sharnouby 等（1985）］。

本书计算结果比其他两种计算方法的计算结果相比略小，这是由于本书计算方法考虑了桩在土中的“加筋效应”。

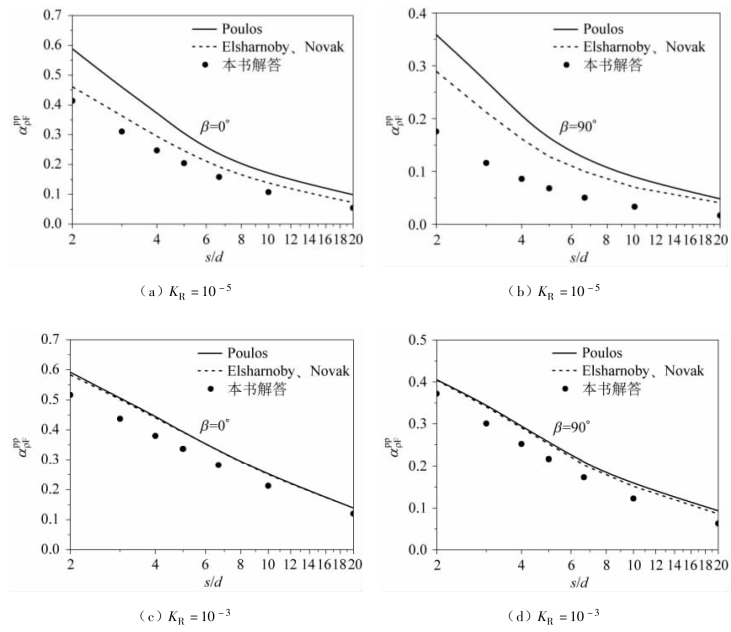
图3.13　仅受水平力作用下两桩相互作用系数的比较

4.与Chow（1987）、Randolph（1981）和Poulos（1971b）解答的对比

图3.14 给出了与Chow（1987）、Randolph（1981）和Poulos 等（1980）解答的对比结果。不同的桩土弹性模量比Ep/Es= 80、8 000，不同的荷载作用方向线偏离角β = 0°、90°，桩长细比L/d = 25。在Randolph（1981）、Poulos（1971b）和本书的解答中土的泊松比为μs= 0.5，在Chow（1987）的解答中土的泊松比为μs= 0.499。Randolph（1981）采用近似表达式法与Poulos 等（1980）的弹性理论解答较接近，Chow（1987）采用有限单元法计算刚度法中的影响系数，比Randolph（1981）和Poulos（1971b）的计算结果都小，而本书计算方法与Chow（1987）的计算结果较为接近。

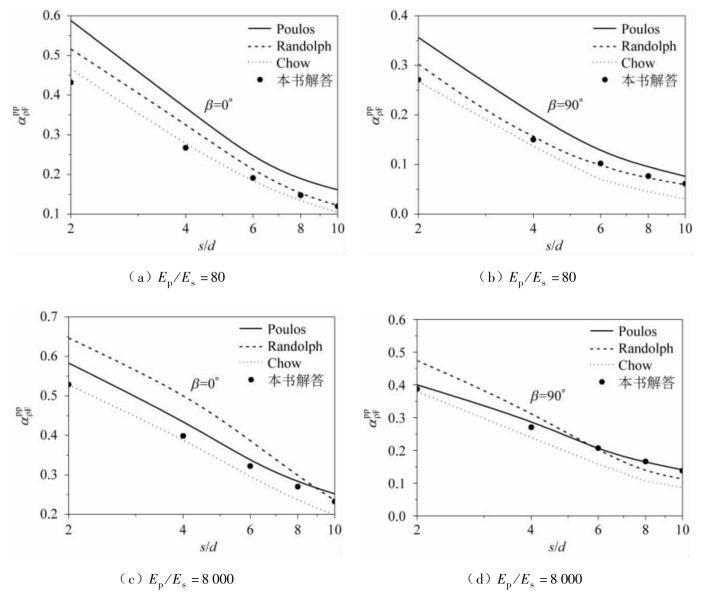
图3.14　仅受水平力作用下两桩相互作用系数的比较