高承台桩基位移系数解法及其影响因素

1.分段数对精度的影响

为了确定桩身分段数对两根桩之间相互作用系数计算精度的影响，图3.2 给出了仅受水平力的桩顶自由桩的位移相互作用系数与桩体分段数之间的关系，桩体分段数表示为：n = δL/d，其中，δ 表示单位桩长L/d 的分段数。计算中桩心距s/d = 4，在不同的桩土模量比Ep/Es= 10、1 000、桩长细比L/d = 20、60、80、100、土的泊松比μs= 0.15、0.3、0.49 情况下，考察了单位桩长分段数δ 对仅受水平力的桩顶自由桩的位移相互作用系数计算精度的影响。

图3.2　桩分段数对相互作用系数的影响

比较图3.2a ～d 可以得出如下一些结论：

（1）桩长细比L/d 对数值计算精度的影响不明显，图中所示四种情况下数值计算结果呈现出相同的规律，这个结论与曹明（2007）的竖向荷载作用下的分析结果一致。

（2）地基土泊松比对数值计算精度在δ ＞2 时影响并不明显，这个结论与曹明（2007）的竖向荷载作用下的分析结果一致。

但在δ ＜2 时，与曹明（2007）的竖向荷载作用下的分析结果不一致。在竖向荷载作用下，地基土泊松比对数值计算精度有明显影响。随着泊松比μs的增大，数值计算精度收敛速度减小。这是因为在Fredholm 积分方程中考虑到应变的间断性，在积分方程中有项，当μs接近于0.5 时，这项趋近于零，从而增大数值计算中的误差，通过增加桩的分段数，可以减小这个误差，使数值解答趋于稳定。而水平荷载作用下的位移相互作用系数求解方程中，没有此项，因此，泊松比的变化对计算精度影响不大。

（3）桩土弹性模量比Ep/Es在δ ＞2 时对计算精度影响并不明显，在δ ＜2 时有比较明显的影响，随着桩土弹性模量比Ep/Es的增大，数值计算精度收敛速度显著减小。这是由于随着桩土弹性模量比Ep/Es的增大，Fredholm 积分方程中有一项κ 趋近于零，与曹明（2015）的分析结果一致。

（4）综合以上分析以及陆建飞（2000）、梁发云（2004）和曹明（2015）的分析结果，当桩的分段数δ≥3 时，数值结果已经稳定。虽然说桩体分段数越多，计算精度越高，但随着计算精度的提高，计算耗时也在增加。

2.与Leung 等（1987）、Randolph（1981）和Poulos（1971b）解答的对比

为了说明本书计算结果与其他学者解答的区别，图3.3 给出了与Poulos（1971b）、Randolph（1981）和Leung 等（1987）解答的对比结果。土的泊松比μs= 0.5，刚度系数KR=EpIp/EsL4= 10-5，桩长细比L/d = 25。本书计算结果与Leung 等（1987）的计算结果相差不大，而Poulos（1971）与Randolph（1981）的计算结果基本相同，这是因为本书在计算中，考虑了桩土分离以后桩所在位置孔洞的存在，在理论上更加严密，误差更小。Leung 等（1987）采用荷载—位移曲线法计算桩—土相互作用。

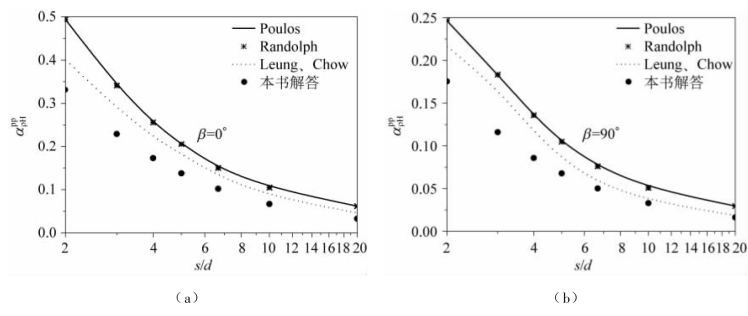
图3.3　仅受水平力作用下两桩相互作用系数的比较

3.与Poulos（1971b）和曹明（2015）解答的对比

图3.4 给出了与Poulos（1971b）和曹明（2015）解答的对比结果。Poulos（1971b）给出了在均质半无限空间体中，相对于各种桩长细比L/d，桩身刚度系数KR= EpIp/EsL4和桩间距s/d 的两根摩擦桩之间的相互作用系数。在Poulos（1971b）和本书解答中土的泊松比μs=0.5，在曹明（2015）有限单元法的解答中土的泊松比μs= 0.49。可以看出，包括本书在内的三种求解方法对两根摩擦桩相互作用系数的计算结果都有区别。这是由于在计算桩—土相互作用时采用的计算模型不同。Poulos（1971b）的计算结果相对于本书的计算结果要偏大，而与曹明（2015）有限元解答相差不大，这是因为本书在计算中，考虑了桩土分离以后桩所在位置孔洞的存在，在理论上更加严密，误差更小。

图3.4　相互作用系数随桩距的变化(www.xing528.com)

4.与Poulos（1971b）解答的进一步对比

为了进一步说明本书计算结果与Poulos（1971b）解答的区别，取土的泊松比为μs= 0.5，不同的桩长细比L/d =25、100，不同的荷载作用方向线偏离角β =0°、90°，不同的桩身刚度系数KR= EpIp/EsL4= 10-5、10-1情况下两根摩擦桩之间仅受弯矩作用下的位移相互作用系数进行比较。

从图3.5 和图3.6 可以看出，当桩身刚度系数较大时（KR= 10-1），两种计算方法的计算结果相差较小，而当桩身刚度系数较小时（KR= 10-5），本书计算结果比Poulos（1971b）的解答都小，这是由于本书在计算两根桩之间的相互作用系数时，考虑了桩在土中的“加筋效应”。基于Mindlin 解计算桩间相互作用时，仅仅对各桩变形简单叠加而未考虑桩的存在对地基上变形所带来的影响从而过高地估计了桩的相互作用，而相邻桩的存在有减少相应桩身周围土体水平位移的作用。这种作用，就叫“加筋效应”。本书通过虚拟桩来考虑桩间这种相互作用，因此本书的解答更为合理。

图3.5　仅受弯矩作用下相互作用系数随桩距的变化

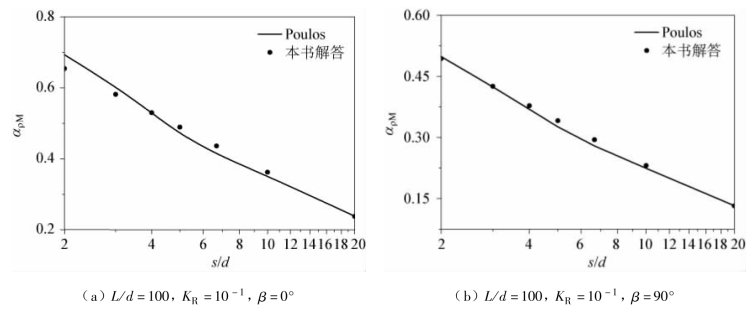
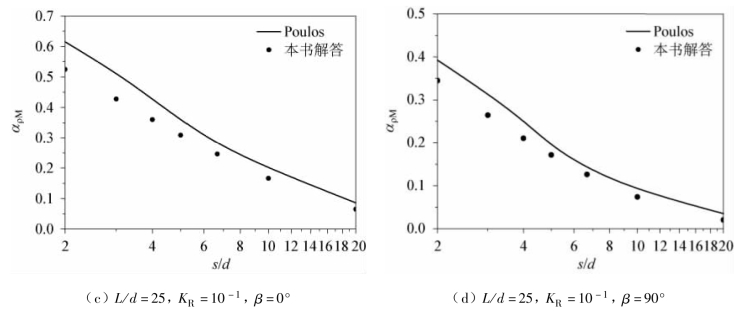
图3.6　仅受弯矩作用下相互作用系数随桩距的变化

5.与El Sharnouby 等（1985）和Poulos（1971b）解答的对比

图3.7　仅受水平力作用下两桩相互作用系数的比较

图3.7 给出了与El Sharnouby 等（1985）和Poulos（1971b）解答的对比结果。土的泊松比μs= 0.5，不同的刚度系数KR= EpIp/EsL4= 10-5和10-3，桩长细比L/d = 25。El Sharnouby 等（1985）采用结构刚度与土刚度相结合的刚度法计算桩—土相互作用，对于柔性桩，Poulos（1971b）的计算结果比El Sharnouby 等（1985）的计算结果大20%，但当El Sharnouby 等（1985）采用与Poulos（1971b）相同的计算单元数时，两种计算方法的结果接近［El Sharnouby 等（1985）］。

本书计算结果比其他两种计算方法的计算结果略小，这是由于本书计算方法考虑了桩在土中的“加筋效应”。

6.与Chow（1987）、Randolph（1981）和Poulos（1971b）解答的对比

图3.8 给出了与Chow（1987）、Randolph（1981）和Poulos（1971b）解答的对比结果。不同的桩土弹性模量比Ep/Es= 80、8 000，不同的荷载作用方向线偏离角β = 0°和90°，桩长细比L/d = 25。在Randolph（1981）、Poulos（1971b）和本书的解答中土的泊松比为μs= 0.5，在Chow（1987）的解答中土的泊松比为μs= 0.499。对于刚性桩，即桩土弹性模量比Ep/Es=8 000 时，Randolph（1981）采用近似表达式法与Poulos 等（1980）的弹性理论解答较接近，Chow（1987）采用有限单元法计算刚度法中的影响系数，比Randolph（1981）和Poulos（1971b）的计算结果都小，而本书计算方法与Chow（1987）的有限元计算结果较为接近。

图3.8　仅受水平力作用下两桩相互作用系数的比较