Fredholm积分方程的建立与高承台混合桩基础位移系数解法

图3.1 所示为半空间土体中两根直径d、弹性模量Ep和长度L 分别相等的桩B′1和B′2，桩体的横截面积都为A。水平向荷载作用下两根桩之间的桩心距为s，连接桩中心线与荷载作用方向线的夹角为β，称为偏离角。设两根桩桩顶分别作用大小相等的单位水平力V（0）或弯矩M（0），将真实桩分解为虚拟土B 和虚拟桩B*1、B*2。由于两根桩的受力性能相同，为了便于分析，以第1 根桩为例，该虚拟桩的弹性模量为

式中，E 为虚拟桩的弹性模量，Es为土的弹性模量。

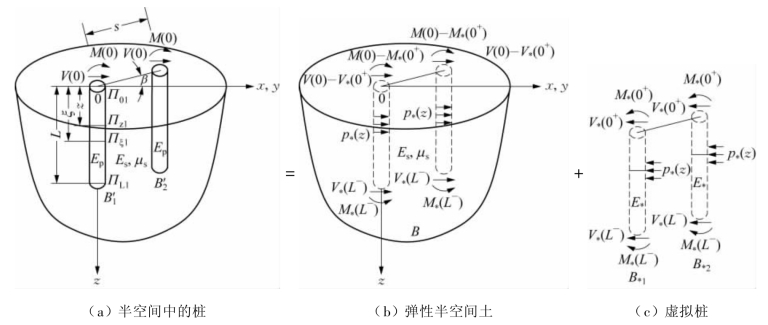
图3.1　两根水平受荷桩的计算模型

根据梁的伯努利—欧拉的挠度理论，图3.1 中所示虚拟桩B 的挠度曲线微分方程为

虚拟桩的平衡方程为

根据Reissner（1940）、Muki 等（1968）假设桩两端通过集中力的方式直接传递给桩周围的土，不考虑桩身与土之间的摩擦力。图3.1c 表示作用在虚拟桩B 上的外力：①-p（z）表示半空间扩展土作用在虚拟桩单位长度上的力；②V（0 +）、-M（0 +）分别表示直接作用在虚拟桩桩顶上的剪力和弯矩；③-V（L -）、M（L -）分别表示作用在桩底上的剪力和弯矩。根据力的作用与反作用原理，作用在半空间扩展土B 上的力包括：①p（z）表示虚拟桩作用在半空间扩展土单位长度上的力；②V（0）-V（0 +）、-［M（0）-M（0 +）］分别表示真实桩在截面Π0上直接作用在半空间扩展土上的剪力和弯矩；③V（L -）、-M（L -）分别表示虚拟桩在截面ΠL上作用在半空间土上的剪力和弯矩。Pak（1989）进一步假定桩身横截面发生小的旋转，则由真实桩的底端直接传递给虚拟桩的弯矩以及真实桩在截面Π0上直接作用在半空间扩展土上的弯矩可以忽略不计，即

半空间扩展土中桩中心轴线上的点X =（0，0，z）在x 方向上的位移为

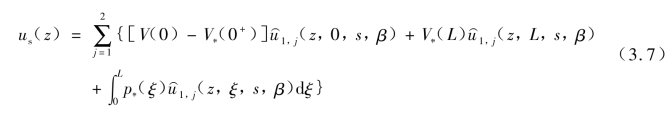
式中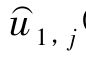，z，ξ，s，β）表示对于每一点z ∈［0，L］和ξ ∈［0，L］，第j 根桩所在位置弹性半空间土任意截面Πξj处作用合力为单位力的均布荷载时在第1 根桩所在位置的弹性半空间土任意截面Πz1圆心处所产生的水平向位移，其值可由Mindlin 基本解进行积分得到。

虚拟桩的位移与半空间扩展土的位移协调，所以在虚拟桩中心轴线上虚拟桩的位移与半空间扩展土的位移相等，即

由式（3.7）和位移协调条件式（3.8），虚拟桩的位移可以表示为

利用式（3.4），式（3.9）可以写为(www.xing528.com)

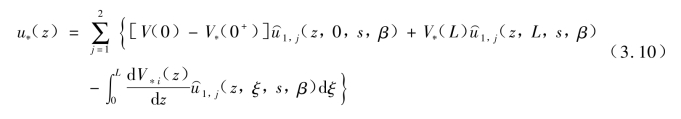
对式（3.10）中右边最后一项进行分部积分，并由式（3.3）可以得到

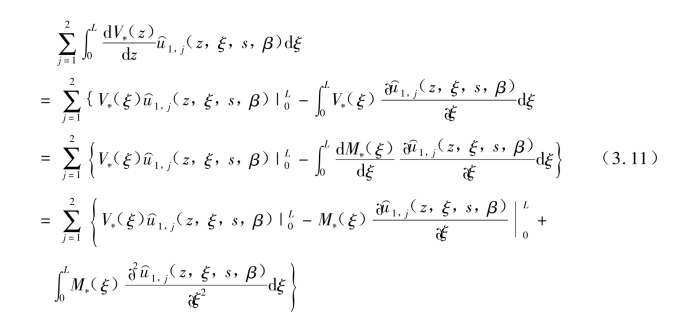
利用式（3.5）和式（3.6），并考虑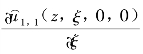的间断性，式（3.11）可以写为

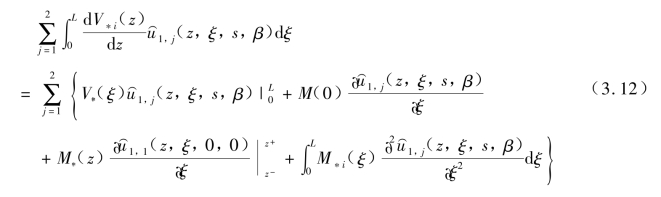
将式（3.12）代入式（3.10）并化简，则得到

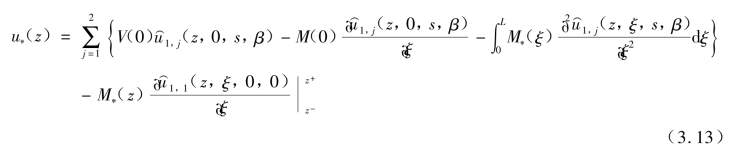
式中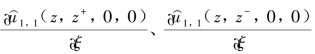，分别表示荷载作用在第1 根桩平面Πξ分别从上侧和下侧无限趋近第1 根桩Πz截面时所引起的Πz截面处圆心的水平向应变。

假设第1 根虚拟桩u（z）为

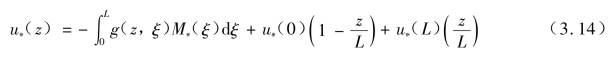
式中，

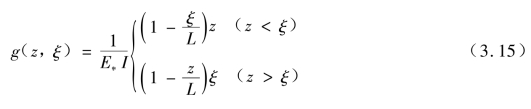
为了进行无量纲分析，假设以下参数

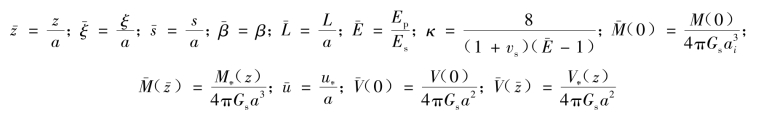
式中，Gs和vs分别是土的剪切模量和泊松比。由式（3.13）、式（2.20）和式（3.14）可得到用无量纲参数表示的控制方程为

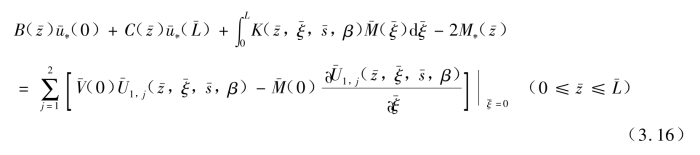
式中，

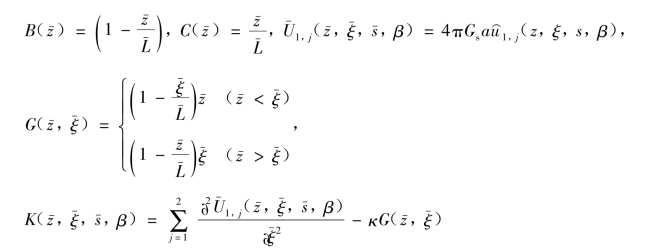
式（3.16）就是求解第i 根桩顶在不同水平向荷载作用下混合桩型桩基问题所需要的第二类Fredholm 积分方程，与式（3.5）和式（3.6）联立可以直接求解，其中待求的未知量为虚拟桩的桩身弯矩、桩顶水平位移和桩底的水平位移。