量子宇宙中的恒星死亡

当恒星死亡时，许多恒星最终会变成极其致密的核物质球，与电子的海洋混合在一起，被称为“白矮星”。这将是我们的太阳在50亿年后耗尽核燃料时的命运，也是银河系中95%以上恒星的命运。只需用纸笔和一点思考，就能计算出这些恒星的最大质量。于1930年第一次完成这项计算的是苏布拉马尼扬·钱德拉塞卡，他使用量子理论和相对论做出了两项非常明确的预测。其一，不出意外会有白矮星这样的东西：一个因泡利不相容原理而抵抗住自身引力挤压的物质球。其二，如果把注意力从那张涂满整篇的理论草稿纸上移开，抬头凝视夜空，那么我们应该绝不会发现质量超过1.4倍太阳质量的白矮星。这些都是极其大胆的预测。

今天，天文学者已经将约10000颗白矮星编入目录。大部分的质量在0.6倍太阳质量左右，而质量的最大纪录正好低于1.4倍太阳质量。“1.4”这个数字，是科学方法的胜利。它依赖于对核物理、量子物理和爱因斯坦狭义相对论的理解，是20世纪物理学交叉分枝的成果。要算出它，还需要在本书中曾遇到过的大自然的各基本常数。在本章结束时，你会了解到，最大质量是由这个比率

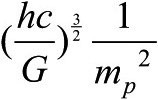
所决定的。仔细看看我们刚刚写下的东西：它由普朗克常数、光速、牛顿引力常数和质子质量所决定。我们可以用基本常数的这个组合来预测一颗垂死恒星的质量上限，这是多么美妙。在比率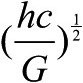中，出现了引力、相对论和作用量量子的三方组合；它称为普朗克质量，而代入数值后，它大约55微克，大致是一粒沙子的质量。所以，令人震惊的是，钱德拉塞卡质量是在对两种质量的沉思中得出的，一种是一粒沙的质量，另一种是一个质子的质量。从这样微小的数字中，出现了一个新的大自然的质量尺度：一颗垂死恒星的质量。

关于钱德拉塞卡质量是如何得出的，笔者可以做一份宽广的概述，但我们想要做得更多一点：我们想要描述实际的计算，因为这才能真正让人脊背发凉。我们无法算出精确的数字（1.4倍太阳质量），但可以接近它，并看到专业物理学者如何使用一系列精心设计的逻辑步骤，在过程中引用人所皆知的物理学原理，得出深刻的结论。并不会有信仰之跃；相反，我们将保持头脑冷静，缓慢而不可阻挡地被引向最激动人心的结论。

我们的出发点是：“恒星是什么？”一个非常近似的说法，可见宇宙是由氢和氦组成的，它们是大爆炸后最初几分钟内形成的最简单的两种元素。经过大约五亿年的膨胀，宇宙的温度已经足够低，气体云中密度稍高的区域可以在自身引力的作用下开始团聚成块。这些就是星系的种子，在其中较小的团块内，第一批恒星开始形成。

这些第一批原恒星（proto-star）中的气体，随着自身的坍缩而变得愈来愈热。用过自行车打气筒的人都知道，压缩气体会使其变热。当气体温度达到100000摄氏度左右时，电子就不能再保持在氢和氦核的轨道上，原子就被撕裂，留下由裸原子核和核电子组成的热等离子体^[258]（plasma）。炽热气体试图向外膨胀，抵抗进一步坍缩；但对于足够大的团块，引力会胜出。由于质子带正电荷，它们会互相排斥；但随着引力坍缩继续，温度不断升高，质子的运动速度会愈来愈快。最终，在几百万摄氏度的温度下，质子的运动速度足够快，足以使它们充分靠近，而弱相互作用开始发挥作用。这时，两个质子就可以发生反应；其中一个质子自发转变成中子，同时发射出一个正电子和一个中微子（和图11.3中描绘的完全一样）。摆脱了电排斥作用，质子和中子就能在强相互作用下结合，产生氘核。这个过程会释放出巨大的能量，因为就像氢分子的形成一样，把东西结合在一起会释放出能量^[259]。

以日常标准来看，一次核聚变释放的能量并不多。100万次质子-质子核聚变所产生的能量，大约相当于一只飞行蚊子的动能，或者一只100瓦灯泡在一纳秒内辐射的能量。但是，这在原子尺度上就是巨大的，并且请记住，我们是在讨论一团坍缩气体云的稠密核心，其中每立方厘米有约10²⁶个质子。如果一立方厘米内的所有质子都融合成氘核，就会释放出10¹³焦耳的能量，足以为一座小镇供电一年。

两个质子融合成一个氘核，是聚变大串联的开始。氘核本身也希望与第三个质子融合，造出轻量版氦核（称为氦-3），并释放出一个光子；而这些氦核结对，聚变生成一个普通版氦核（称为氦-4），并释放出两个质子。在每个阶段，聚变释放出愈来愈多的能量。而且，作为一个不错的衡量标准，在链式反应开始时就发射出来的正电子，也迅速与周围等离子体中的一个电子湮灭，生成一对光子。所有这些释放出来的能量，造就了一团由光子、电子与原子核构成的炽热气体，撑起了落向中心的物质，阻止了进一步的引力坍缩。这就是一颗恒星：核聚变在核心燃烧核燃料，这就产生了向外的压力，使恒星从引力坍缩中稳定了下来。

当然，可供燃烧的氢燃料有限，最终会耗尽。如果不再有能量释放，就不再有向外的压力；引力再次主导变化，而恒星恢复了被推迟的坍缩。如果恒星质量足够大，恒星将加热到约1亿摄氏度左右的温度。在这个阶段，氢燃烧阶段产生的废物氦被点燃，聚变产生碳核氧，引力坍缩再次暂时停止。

但如果恒星质量不足以启动氦聚变会怎么样？对于质量小于太阳质量一半的恒星就会如此；对于它们，会发生一些非常戏剧性的事情。恒星在收缩过程中被加热，但在核心到达1亿摄氏度之前，有其他东西阻止了坍缩。这个东西就是电子由于受泡利不相容原理的控制而施加的压力。前面学到，泡利原理对理解原子如何保持稳定至关重要，它是物质特性的基础。这里是它的另一重功效：泡利原理解释了致密星的存在，尽管它们不再燃烧任何核燃料。这是怎么做到的呢？

随着恒星被压扁，其中的电子也被限制在更小的体积内。可以用恒星内电子的动量p和与之关联的德布罗意波长h/p来表示它。具体来说，这个粒子只能用一个至少与其波长一样大的波包来描述^[260]。这意味着，当恒星密度足够大时，电子一定是相互重叠的，即我们不能想象它们是由孤立的波包所描述。这又意味着量子力学效应，特别是泡利原理，对于描述电子非常重要。具体来说，它们被紧密挤压在一起，以至于两个电子试图占据同一空间区域；由泡利原理可知，它们会抵抗这一点。因此，在垂死的恒星中，电子希望相互避开，这可以提供一种抵抗进一步引力坍缩的刚性。

这是最轻恒星的命运，而像太阳这样的恒星呢？在几段之前我们描述过，它们会将氦烧成碳和氧。但当它们的氦也耗尽时会怎么样呢？它们也得在自身引力作用下开始坍缩，这意味着电子会被挤压到一起。就像较轻的恒星一样，泡利原理最终会发挥作用，阻止坍缩。但是，对于质量极大的恒星来说，即使泡利不相容原理也有其局限性。随着恒星坍缩，电子被挤压得愈来愈近，因此恒星核心被加热，电子运动得更快。当恒星质量足够大时，电子的运动速度极快，接近光速，这时就会出现新的情况。当电子接近光速时，它们能施加的抵抗引力的压力就会减小，以至于无法抵抗。它们不再能战胜引力并阻止坍缩。我们在这一章的任务就是计算这种情况会在何时发生，并且已经给出了重点。对于质量大于1.4倍太阳质量的恒星，电子输了，引力获胜。

这些就是对我们计算的基础的概述。现在我们可以往下走，并忘掉所有核聚变的事情，因为我们的兴趣已经不在燃烧的恒星上了。相反，我们希望了解死亡恒星内部的情况。想要知道，被挤压的电子所产生的量子压力是如何平衡引力，以及如果电子运动速度过快，这种压力是如何变小的。因此，我们研究的中心是一个平衡游戏：引力与量子压力的对决。如果能使其平衡，就能得到白矮星，但如果引力获胜，就会发生灾难。

虽然与计算无关，但我们不能在紧要关头置之不理。一颗大质量恒星内爆后，它还有两种选择。如果它质量不太大，则恒星会继续挤压质子和电子，直到它们也融合产生中子。具体来说，一个质子和一个电子自发转变成一个中子，并发射出一个中微子；这同样是通过弱相互作用完成。这样，恒星就无情地转化成一个由中子构成的小球。用俄国物理学家列夫·朗道^[261]（Lev Landau）的话来说，恒星转化成“一个巨大的原子核”。朗道在他1932年的著作《论恒星的理论》中写下了这些话，就在这书交稿印刷的同一个月，詹姆斯·查德威克^[262]（James Chadwick）发现了中子。如果说朗道预言了中子星的存在，可能言过其实；但是，他以超凡的先见之明，肯定预见到了什么类似的东西。也许功劳该归于沃尔特·巴德^[263]（Walter Baade）和弗里茨·兹威基^[264]（Fritz Zwicky），他们于次年写道：“我们慎重地提出这个观点：超新星^[265]（supernova）表示普通恒星向中子星的转化；在最终阶段，它由极紧密的中子所组成。”人们认为这个观点极其古怪，以至于有人在《洛杉矶时报》上发表了戏仿漫画（见图12.1）。直到1960年代，中子星仍只是理论上的有趣发现。

图12.1：1934年1月19日《洛杉矶时报》上的漫画。

1965年，安东尼·休伊士^[266]（Antony Hewish）和塞缪尔·奥科耶^[267]（Samuel Okoye）发现了“蟹状星云中一个不寻常的高射电亮度温度（radio brightness temperature）源的证据”，尽管他们未能确定这是一颗中子星。支持这一结论的证据于1967年由约瑟夫·什克洛夫斯基^[268]（Iosif Shklovsky）发表，以及不久之后，经过更详细的观测，由约瑟琳·贝尔^[269]（Jocelyn Bell）和休伊士本人再次发表。作为宇宙中最奇特的天体之一，这第一颗中子星，后来被命名为“休伊士-奥科耶脉冲星^[270]（pulsar）”。有趣的是，早在一千年前，那颗创造了休伊士-奥科耶脉冲星的超新星就曾经被天文学家观测到。1054年的这颗有史以来最亮的超新星被中国天文学家观测到^[271]，以及如一幅著名的悬崖壁画所示，也被美国西南部、查科峡谷^[272]的居民观测到。

我们还没有谈到，这些中子是如何抵抗引力并防止进一步坍缩的，但你大概能猜到是怎么回事。中子（类似电子）受泡利原理奴役，它们也能阻止进一步的坍缩。所以就像白矮星一样，中子星也代表了恒星生命可能的终点。就我们的故事而言，中子星是一条岔路；但不能不提到，中子星是我们奇妙宇宙中的一些非常特殊的物体：它们是城市大小的恒星，密度大到一茶勺的量就有一座山那么重，完全由自旋1/2粒子间的天然厌恶所支撑。

对于宇宙中质量最大的恒星，连其中的中子都已接近光速运动，就只剩下了一个选择。灾难等待着降临到这样的巨星，因为中子已经无法产生足够的压力来抵抗引力。目前已知的物理机制还无法阻止一个超过三倍左右太阳质量的恒星向自身塌陷，最终就成了黑洞（black hole）：一个众所周知物理定律崩坏的地方。大自然的法则大概不会停止运行，但要正确理解黑洞内部，需要一个引力的量子理论，它现在还不存在。

现在是时候回到正题，专注于我们的双重目标了：证明白矮星的存在，并计算钱德拉塞卡质量。我们知道要如何做：必须平衡电子压力与引力。这仅用头脑可计算不出来，所以制订一个行动方案比较好。下面就是方案；它相当长，因为我们要先弄清一些背景细节，为实际计算做好准备。

第一步：需要确定在恒星内部由于电子高度压缩而产生的压强是多少。你可能会奇怪，为什么我们不担心恒星内部的其他东西——原子核和光子呢？光子不受泡利不相容原理的影响，并且只要时间足够长，它们总会离开恒星。它们没法对抗引力。至于原子核，半整数自旋的原子核是受泡利不相容原理约束的，但（后面会看到）它们的质量较大，这意味着它们施加的压力比电子小，我们可以安心地忽略它们对平衡游戏的贡献。这极大地简化了问题——电子压力就是所需的一切，这也是我们将要关注的。

第二步：在弄清楚电子压力后，我们需要完成平衡游戏。要如何继续进行，也许并不明显。嘴上会说“引力向内拉，电子往外推”，但要给这句话添上一个数可就是另一回事了。

恒星内部的压力是变化的；中心的压力更大，而表面的更小。压力梯度的存在至关重要。想象恒星内部某处有一个恒星物质组成的立方体，如图12.2所示。引力会将立方体拉向恒星中心，而我们想知道的是电子产生的压力要如何抵消它。电子气体^[273]中的压强，对立方体的六个面都施加了一个力，它等于该面上的压强^[274]乘以该面的面积。这个陈述很精确；此前我们都在用“压力”一词，若你有足够的直观认识，就会知道高压气体比低压气体的“推力”更大。每个给瘪轮胎打过气的人都知道这一点。

图12.2：恒星内部某处的一个小立方体。箭头表示恒星中的电子对立方体施加的压力。

想要正确理解压力，就需要暂时转入我们更熟悉的领域。继续以轮胎为例，物理学者会说，轮胎瘪了，是因为胎内气压过低，若轮胎不变形，就不足以支撑车的重量；这就是为什么总得打足气。我们可以继续计算，如果希望轮胎与地面接触长为5厘米，则质量为1500kg的汽车的正确胎压是多少，如图12.3所示；又到了粉笔灰时间。

图12.3：轮胎在承受车重时轻微变形。

如果轮胎有20厘米宽，而我们希望轮胎与路面接触有5厘米长，则轮胎与地面的接触面积是20×5=100平方厘米。所需要的胎压还不知道——这是我们要计算的——所以我们用符号P来表示它。需要知道轮胎内空气对地面施加的向下的力。这等于压强乘以轮胎与地面接触的面积，即P×100平方厘米。我们应该将其乘以4，因为车有4个轮胎：P×400cm²。这就是轮胎内气体对地面施加的合力。可以这样想：胎内空气分子不断冲击地面（说得严谨一点，它们是在冲击接触地面的轮胎橡胶，但这并不重要）。地面通常不会让步，它在这种情况下会以大小相等但方向相反的力（所以确实用到了牛顿第三定律）推回去。汽车被地面抬起，又被重力拉下；由于它既未沉入地下也没跃入空中，我们知道这两个力一定是相互平衡的。因此，可以在P×400cm²的向上推力与向下的重力之间写下等号。后者就是汽车的重量，而我们知道如何用牛顿第二定律来计算它，F=ma，其中a是地球表面的重力加速度，等于9.81m/s²。所以重量是1500kg×9.8m/s²=14700牛顿（1牛顿等于1kg·m/s²，大致相当于一个苹果的重量）。这两个力相等，意味着：

P×400cm²=14700N

这个方程很容易解：P=(14700/400)N/cm²=36.75N/cm²。36.75牛顿每平方厘米的压强，可能不是一种非常常见的胎压陈述方式，但可以把它转化成更熟悉的“巴”（bar）。1巴是标准大气压，等于100000牛顿每平方米。一平方米有10000平方厘米，所以每平方米100000牛顿相当于每平方厘米10牛顿。因此，所需的胎压为36.75/10=3.7巴（或53磅每平方英寸——你也可以自行计算）。还可以利用我们的公式推断，如果胎压降低50%至1.85巴，则轮胎与地面的接触面积将增至2倍，从而使轮胎更瘪。在复习完压强课程后，我们可以回到图12.2中的恒星物质小立方体上了。

如果立方体的底面更接近恒星的中心，则这个面所受的压力应该比顶面所受的压力要大一些。这个压力差在立方体上产生的合力，想把立方体推离恒星的中心（图中“向上”），而这正是我们想要的，因为同时立方体会被重力拉向恒星的中心（图中“向下”）。如果能搞清楚如何平衡这两个力，那么我们对恒星就会有更多了解。但这知易行难，因为虽然第一步能算出立方体被电子压力向外推的程度，但我们还得算出重力向相反方向拉的程度。顺便一提，无需担心立方体侧边的压力，因为侧边到恒星中心距离相等，所以左侧的压力会与右侧平衡，这就保证了立方体不会向左或向右移动。

要计算出立方体所受的引力，需要利用牛顿的万有引力定律；它告诉我们，恒星内每一块物质对这个小立方体的拉力都是愈远愈小。所以，较远的物质比较近的拉力要小。不同位置的恒星物质对立方体的引力大小不同，取决于距离。要处理这个问题，看似有些棘手，但我们至少能在原则上看出来，应该把恒星切成很多小块，然后计算出对每一块小立方体的力。幸运的是，我们不必去想象真的把恒星切碎，因为可以利用一个非常漂亮的成果。高斯公式（以传奇的德国数学家卡尔·弗里德里希·高斯^[275]的姓氏命名）告诉我们：(a)可以完全忽略比小立方体到恒星中心的距离更远的小块；(b)所有比小立方体到恒星中心更近的小块，其净引力效应正好和这些小块全都挤在恒星的正中心时一样。利用高斯公式并结合万有引力定律，我们可以说，小立方体受到将其拉向恒星中心的力，它等于：

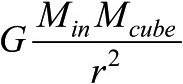
其中M_in是恒星中以立方体与中心距离为半径的球体内部的质量，M_cube是立方体的质量，r是立方体到恒星中心的距离（G是牛顿引力常数）。例如，如果小立方体位于恒星表面，则M_in就是恒星的总质量。对于其他的所有位置，M_in都比这个质量小。

我们现在取得了一点进展，因为要平衡小立方体上的力（请注意，这是为了让立方体不运动，进而阻止恒星爆炸或坍缩^[276]），就要求

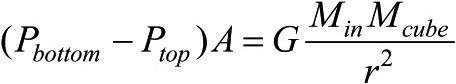
（1）

其中P_bottom和P_top是电子气体在小立方体上下两面施加的压强，A是立方体每个面的面积（记住，压力等于压强乘以面积）。我们把这个方程标记为“(1)”式，因为它非常重要，我们要经常引用它。

第三步：泡一杯茶并自鸣得意，因为在第一步之后，我们就会计算出压强P_bottom和P_top，而第二步就弄清楚了如何使得二力平衡。但真正的工作还没有来，因为还需要实际执行第一步，并确定(1)式中等号左侧的压强差。这就是接下来的任务。

想象一颗恒星，内部挤满了电子和其他东西。电子是如何分布的呢？我们来把注意力集中在一个“典型”电子身上。我们知道，电子服从泡利不相容原理，这意味着在空间的同一区域不可能找到两个相同的电子。对于恒星中被笔者称为“电子气体”的电子海洋，这又意味着什么呢？因为电子之间必然是相互分离的，所以可以假设，每个电子都孤独地位于恒星内一个微小的假想正方体内。实际上，这并不完全正确，因为我们知道电子有两种类型“自旋向上”和“自旋向下”，而泡利原理只禁止相同的粒子靠得太近，也就是说一个正方体内可以容纳两个电子。这与电子不服从泡利原理的假想情况会形成对比。在那种情况下，“虚拟容器”中将不会有多余两个电子被束缚的情况。相反，它们可以分散开来，享受更大的活动空间。其实，如果我们忽略电子之间以及电子和恒星内其他粒子的相互作用，则它们的活动空间将不受限制。

我们知道当一个量子粒子被束缚时会怎么样：根据海森伯不确定性原理，它会四处跃动；而且被束缚得愈紧，跃得愈多。也就是说，随着白矮星前身的坍缩，其中的电子也被束缚得愈来愈紧，而这让它们愈发躁动。正是由于它们的躁动所施加的压力，才会阻止引力坍缩。

我们可以做得比说的更好，因为可以用海森伯不确定性原理来确定电子的典型动量。具体来说，如果将电子约束在尺寸为Δx的区域内，则它会按照典型动量P~h/Δx四处跃动。实际上，在第四章中曾经论证过，这更像是动量的上限，而典型动量是零到这个值之间的某个数。这条信息先记下来，之后会用到。知道了动量，就能立刻了解两件事。第一，如果电子不服从泡利原理，则它们就不会被约束在Δx大小的区域内，而会是一个大得多的区域。这又会导致抖动得更少，意味着压强更小。所以，泡利原理是如何进入游戏的，就很清楚了：它挤压电子，使得电子通过海森伯不确定性原理进行特强抖动。过一会儿，我们会把这个超强抖动的想法用公式表达出来，算出压强；但现在我们应该谈谈可以了解的第二件事。因为动量p=mv，所以抖动的速度还反比于质量；故而电子的四处跳动，与同样构成恒星的原子核的相比，要有力得多；这就是原子核施加的压力不重要的原因。那么，我们要如何用电子的动量算出类似电子所构成的气体的压强呢？

首先要做的是，计算出包含这对电子的小正方体有多大。它的体积是（Δx）3；由于所有的电子都必须装进恒星里，我们可以将这个体积用恒星体积（V）除以恒星内的电子总数（N）来表示。需要正好N/2个容器，来容纳所有的电子，因为每个容器中可以放两个电子。这意味着每个容器所占的体积是V除以N/2，等于2(V/N）。下文中会大量用到N/V这个（恒星内单位体积中的电子数）量，所以我们用一个单独的符号n来表示它。现在可以写下，要容纳下恒星内所有的电子，每个容器的体积得是多少，即（Δx）3=2/n。取等号右侧的立方根，就能算出：

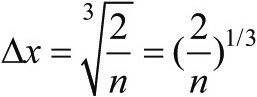
现在可以把这个式子代入到不确定性原理中，得到电子由于量子抖动贡献的典型动量：

（2）

其中～符号表示“大致等于”。显然这有些模糊，因为电子不会以完全相同的方式抖动：有一些比典型值更快，另一些更慢。海森伯不确定性原理并不能告诉我们到底有多少个电子在以这个速度运动，有多少个以那个速度运动。相反，它给出了一个更“宽泛”的陈述，说如果你挤压电子的活动空间，那么它会以大致等于h/Δx的动量抖动。我们就取这个典型动量，并假设所有的电子都这样运动。这样做会损失一点精度，但能极大地简化计算，并且我们思考物理的大方向肯定是正确的^[277]。

现在我们知道了电子的速度，这足以计算出它们对小立方体施加的压力。要看出这一点，想象一队电子以相同的速率（v），共同向一面平面镜的方向前进。它们撞上镜面后又弹回来，再次以相同的速率，向与之前相反的方向运动。我们来计算一下这队电子对镜面施加的力。之后我们可以尝试更现实的计算，其中电子并不都向相同方向运动。这种首先考虑待解决问题的一个简化版本的方法在物理学中非常常见。这样就可以研究物理，而不至于贪多嚼不烂，还能增强信心；在这之后再解决更困难的问题。想象这队电子每立方米中包含n个粒子。为方便论证，假设其截面是圆形，面积为1平方米，如图12.4所示。在1秒钟内，将有nv个电子击中镜面（如果v的单位是米每秒的话）。我们知道，从镜面出发到v×1秒距离，这个范围内所有的电子都将在1秒内撞上镜面，即图中画出的圆柱体内的电子。由于圆柱的体积等于其横截面积乘以长度，因此这个圆柱的体积等于v立方米，而因为每立方米体积内有这队电子里的n个，所以每秒钟有nv个电子击中镜面。

图12.4：一群电子（小点）都朝同一个方向前进。这样尺寸的管子里所有电子每秒钟都会撞到镜子上一次。

当每个电子从镜面上不损失能量地弹回时，其动量的方向会反转，这意味着每个电子的动量改变量为2mv。现在，就像要把一辆行进的巴士停下来并倒行需要一个力一样，要把电子的动量反转也需要一个力。这又得用到艾萨克·牛顿的工作。在第一章中，我们将它的第二定律写成F=ma，但这是更普遍情形的一种特例，即力等于动量的变化率^[278]。因此，整队电子将在镜面上施加合力F=2mv×(nv)，而这是每秒队中电子动量的总变化量。由于电子束的面积为1平方米，这也等于队中电子对镜面施加的压力。

从电子队到电子气只需要向前一小步。电子并不是齐步向着同一个方向前进；必须考虑到，一些电子向上运动，一些向下走，一些向左，等等。最后的净效果是，任何一个方向的压力将减小一个因子6（想想正方体的六个面），变成F=2mv×(nv)/6=nmv²/3。我们可以将式子中的v，用由海森伯原理估计的典型电子速度，即(2)式来代替，从而得到白矮星中电子压强的最终结果^[279]：

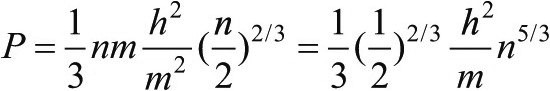
你可能还记得，前面说过这只是近似计算。使用更多的数学算式之后，得到的完整结果是：

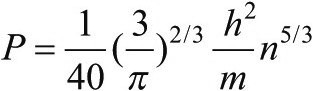
（3）

这是个不错的结果。它告诉我们，恒星内某处的压强，与那里每单位体积内的电子数的5/3次幂成正比。不必担心，在近似处理中，我们没有把比例系数弄对——重要的是，除此以外的其他一切都是对的。事实上，前面已经说过，我们对电子动量的估计可能有点过大，这就解释了为什么我们对压强的估计比真实值要大^[280]。

用电子数密度来表示压强，是一个好的开始；但使用实际的恒星质量密度来表示压强，更符合我们的目的。可以非常安全地假设，恒星的绝大部分质量来自原子核，而非电子（一个质子的质量几乎是电子的2000倍）。我们还知道，恒星中电子的数量必须等于质子的数量，因为恒星是电中性的。为了得到质量密度，需要知道恒星内部每立方米有多少个质子和中子；我们不应该忘记中子，因为它们是核聚变过程的副产品。对于较轻的白矮星，核心主要是氢核聚变的最终产物氦-4，这意味着质子和中子的数量相等。现在需要引入一点记号。原子量A，通常用于计算原子核内质子和中子的总数，而对于氦-4，A=4。原子核中的质子数用符号Z表示，对于氦来说，Z=2。现在我们可以写下电子数密度n与质量密度ρ的关系：

n=Zρ/(m_pA)

而我们假设质子质量m_p与中子质量相同；这对于我们的目的已经足够精确了。m_pA这个量是每个原子核的质量，而p/m_pA则是每单位体积的原子核数量，再用Z乘以这个量就得到了单位体积内的质子数，这就是等式所表达的含义。

我们可以用这个等式代替(3)式中的n；由于n与ρ成比例，所以得出的结果是，压强随着密度的ρ次幂成比例变化。我们刚刚发现的这一突出的物理现象是：

P=κρ^5/3

（4）

而定下压强大小的纯粹数字倒不必太过于担心，这就是我们把它们都绑进符号κ的原因。值得注意的是，κ取决于Z和A之比；因此对于不同种类的白矮星，它的值会有所不同。把一些数绑进一个符号中，有助于“看出”哪些才是重要的。在本例中，这些符号可能会分散我们对要点的注意力，就是恒星中压强和密度的关系。

在继续之前，请注意，量子抖动产生的压强，并不依赖于恒星的温度。它只与恒星受挤压的程度有关。如果考虑到温度，电子会因此而“正常”地颤动，并贡献额外的压强；而恒星愈热，它就颤动得越厉害。我们没有讨论来自这一部分的压强，因为时间不够；并且如果真的去计算，会发现它在大得多的量子压强面前相形见绌。

最后，我们已经准备好将量子压强的表达式代回关键的(1)式，这里值得再写一遍：

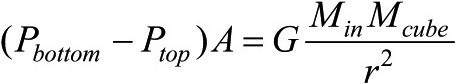(www.xing528.com)

（1）

但这并不像听起来那么容易，因为还需要知道小立方体上下两面的压强差。可以完全用恒星内部的密度来重写(1)式，而密度本来就是随着恒星内的位置不同而变化的（一定得是这样，否则就不会有压强差了），然后就可以尝试通过解方程来确定密度是如何随着到恒星中心的距离而变化的。这么做就要解一个微分方程（differential equation），而笔者希望避免这种程度的数学。相反，我们要更讲策略，想得更努力（并且计算得更少），以便利用(1)式来推导出白矮星的质量和半径之间的关系。

显然，这个小立方体的尺寸和它在恒星中的位置都是完全任意的；我们要得出的关于整体恒星的结论不能依赖于小立方体的细节。我们先来做一些可能看似毫无意义的事情。完全可以用恒星的尺寸来表示立方体的位置和大小。如果R是恒星的半径，则可以将立方体到恒星中心的距离写作r=aR^[281]，其中a是一个介于0和1之间的无量纲（量纲是dimension）数。所谓无量纲，就是说它是纯粹的数，不含有单位。如果a=1，立方体就在恒星的表面；而如果a=1/2，则它在中心到表面一半的位置。类似地，可以用恒星的半径来表示小立方体的尺寸。如果L是立方体的边长，则可以写成L=bR，其中b又是一个纯数；如果希望立方体相对恒星很小，则b也会很小。这里面绝对没有什么深奥的东西；在这个阶段，一切都很明显，乃至看似没有意义。唯一值得注意的是，R是一个十分自然的长度单位，因为没有其他任何跟白矮星有关的长度可以合理地替代它。

我们可以继续用类似的方法困扰自己，用恒星的平均密度来表示立方体所处位置的恒星密度，即写成ρ=fρ，其中f还是一个纯数，而是恒星的平均密度。如前所述，立方体的密度取决于它在恒星内部的位置：如果更接近中心，它的密度就会更大。既然ρ平均密度与小立方体的位置无关，那么f就得与之相关，即f得由距离r所决定，这显然意味着它取决于乘积aR。现在这里是决定剩余计算的关键信息：f是一个纯数，但R不是（因为它度量距离）。这意味着f只能取决于a，而和R毫无关系。这是一个非常重要的结论，因为它告诉我们，白矮星的密度分布曲线是“尺度不变”（scale invariant）的。这就是说，无论恒星的半径是多少，它的密度都会以相同的方式随半径而变化。例如，在距离中心3/4的地方，无论恒星尺寸如何，那里的密度与白矮星平均密度的比值对于所有白矮星都一样。有两种方法可以看出这个结果的关键性，笔者认为应该把它们都展示出来。我们中的一人是这样说的：“这是因为，任何函数，如果是无量纲的，它的变量就必须也是无量纲的；而对于函数f，它依赖于有量纲的r，则能作为其变量的、唯一的无量纲组合是r/R=a，因为R是我们所知唯一具有长度量纲的量。”

另一位笔者觉得下面的话更清楚：“一般而言，f可以由r以复杂的方式决定，而后者即小立方体与恒星中心距离。但为了本段的说明，我们假设它们是简单的成正比，即f∝r。换言之，f=Br，其中B是一个常数。这里的关键是，我们希望f是一个纯数，而r是以（比如说）米为单位。这意味着B必须以1/米为单位，这样长度单位才能互相抵消。那么从结果来看，B会是什么呢？我们不能随意选一些东西，比如‘1米的倒数’，因为这没有意义，与恒星毫无关系。比如说，为什么不选1光年的倒数，并且得到截然不同的正比关系呢？我们手头唯一的长度是R，即恒星的物理半径，所以我们被迫用它来确保f永远是一个纯数。这意味着f只取决于r/R。应该可以看到，如果我们开始时的假设是，比如说f∝r²，也会得出相同的结论。”这些其实和前一位笔者说的一样，只是更长。

这个结论意味着，可以将尺寸为L、体积为L³的小立方体的质量，表示为M_cube=f(a)L³ρ。我们把f写成f(a)，是为了提醒你，f实际上只取决于我们对a=r/R的选择，而与恒星大规模的性质无关。用相同的论证还可以写下M_in=g(a)M这个式子，其中g(a)也只是a的函数。例如，函数g(a)在a=1/2时的值就会告诉我们，具有一半恒星半径的同心球体，其质量占恒星质量的比例；并且它对于所有白矮星都是一样的，与具体的白矮星半径无关，这在前一段已经论证过了^[282]。你可能已经注意到，我们在稳步处理(1)式中出现的各种符号，用无量纲的量（a、b、f和g）乘以只和恒星质量及半径有关的量（恒星的平均密度也由M和R决定，因为ρ=M/V，而根据球体积公式，V=4πR³/3）来代替它们。要完成任务，只需对压强差进行相同的处理；可以写作P_button－P_top=h(a,b)κρ^5/3，其中h(a,b)是一个无量纲的量。h(a,b)由a和b共同决定，是因为压强差不仅取决于小立方体的位置（由a表示），还取决于立方体的大小（由b表示）：较大的立方体，对应的压强差也较大。关键是，和f(a)与g(a)类似，h(a,b)也不能单单与恒星的半径有关。

可以用刚刚推导出的表达式，重新写出(1)式：

(hκρ^5/3)×(b²R²)=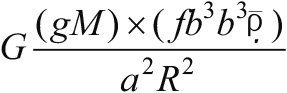

这看起来有点乱，不太像是在一页内就能中大奖。关键之处在于，这是在表达恒星的质量与半径的关系；两者间的具体关系已经近在眼前（或者远在天边，这取决于你的数学能力）。在代入恒星的平均密度[即ρ=M/(4πR³/3)]之后，这个乱七八糟的式子可以整理成

RM^1/3=κ/(λG)

（5）

其中，

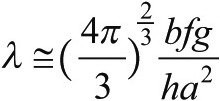
现在的λ只依赖于无量纲的量a、b、f、g和h，这意味着它不由描述恒星整体的量M和R所决定，因此这个式子对于所有的白矮星都是一样的。

如果你担心，当改变a和/或b（这意味着改变小立方体的位置和/或尺寸）时会怎么样，那么你肯定没有领会到这段论证的威力。从表面上看，改变a和b当然会改变λ，这样我们就会得到RM^1/3的不同结果。但这是行不通的，因为我们知道，RM^1/3是取决于恒星整体的，而不是其内部一个、我们可能关心也可能不关心的小立方体的具体性质。这意味着a和b的任何变化，都必须由f、g和h的相应变化所完全补偿，使得λ保持不变。

(5)式相当明确地指出，白矮星可以存在；这是因为我们已经成功地解出了引力-压强的平衡方程[(1)式]。这不是一件平凡的事——因为有可能会发现，平衡方程(1)对于M和R的任何组合都无法被满足。(5)式还作出预言，RM^1/3一定是常数。换句话说，如果我们仰望星空，测量白矮星的半径和质量，就应该会发现，每颗白矮星的半径乘以其质量的立方根，都会得出相同的数。这实在是一个大胆的预言。

笔者刚才展示的论证还可以改进，因为可以准确地计算出λ的数值，但这需要解出一个关于密度的二阶微分方程，而所需的数学技巧对于本书太遥远了。请记住，λ是一个纯数；“它就是它”，可以用一点更高级的数学去算出来。我们没有在这里把它算出来，但这对我们的成就没有丝毫影响：我们已经证明，白矮星可以存在，并且对于其质量与半径的关系做出了预言。在计算出λ之后（可以在家用电脑上完成），并代入κ和G的值，预言的结果是：

RM^1/3=（3.5×10¹⁷kg^1/3m)×(Z/A)^5/3

对于纯氦、碳或氧（Z/A=1/2）组成的核心，等于1.1×10¹⁷kg^1/3m。对于铁核心，Z/A=26/56，式子中的1.1略微变小到1.0。笔者翻阅了学术文献，收集了散布在我们的银河系中的16颗白矮星的质量和半径。对于每一颗，我们都计算出了RM^1/3的值，结果是天文观测给出RM^1/3≈0.9×10¹⁷kg^1/3m。令人激动的是观测和理论比较一致；我们成功地利用泡利不相容原理、海森伯不确定性原理和牛顿引力定律，预言了白矮星的质量-半径关系。

当然，这些数字有一些不确定性（理论值为1.0或1.1，观测值等于0.9）。如果是正确的科学分析方法，现在就会开始讨论理论和实验一致的可能性有多大，但对我们的目的而言，这种层次的分析是不必要的，因为一致得惊人了。我们得以算出这一切，并且误差率仅有约10%，是十分奇妙的。这也是有力的证据，证明我们对恒星和量子力学有了相当的了解。

专业物理学者和天文学者不会就此止步。他们会尽心地详细测试这种理论的认识，为此就需要改进笔者在本章展示的分析。具体来说，改进后的分析会考虑到恒星温度在其结构中确实起到一定作用。此外，电子海在带正电的原子核附近奔涌，但在我们的计算中，电子与原子核之间（以及电子和电子之间）的相互作用被完全忽略掉了。这么做是因为，我们宣称它们对我们的简单处理只产生相当小的修正。这一说法得到了更详细计算的支持，这也是我们的简单处理为何与数据如此一致的原因。

你显然已经学到了很多东西：确定了电子压强能够支持白矮星；设法比较精确地做出预言，如果给恒星增加或减少质量，其半径会如何变化。与急于烧掉燃料的“普通”恒星不同，要注意到白矮星有一个特点，就是增加质量会使其变小。这种情况是因为，我们额外增添的东西会增加恒星的引力，从而使其收缩。从表面上看，(5)式表达的关系似乎意味着需要增加无穷多的质量，恒星才会收缩到完全没有大小。但事实并非如此。如笔者在本章开头所述，重要的是，电子最终会进入极其紧密地聚在一起的阶段，以至于电子的速度开始接近光速，而爱因斯坦的狭义相对论变得重要起来。对我们计算的影响是，必须停止使用牛顿运动定律，而用爱因斯坦的定律来代替。我们将看到，这会产生很大的不同。

我们将会发现的是，随着恒星的质量变大，电子所施加的压强不再与质量密度的5/3次幂成正比，而是随着数密度上升、增长得更慢。稍后我们会进行计算，但可以直接看出这对恒星会产生灾难性的后果。这意味着，当增加质量时，引力照常增加，但压强增加得会更少。恒星的命运，决定于当电子快速运动时，压强随质量密度增加的增长“变慢”了多少。显然，是时候弄清楚“相对论性”电子气的压强了。

幸运的是，我们无需使用爱因斯坦理论的艰深形式，因为要计算以接近光速运动的电子气体中压强所需要的推理，与我们刚才展示的“慢速”电子气体中的推理几乎完全相同。关键的区别在于，动量不再能写成P=mv，因为这已经不正确了。仍然正确的是，电子施加的力仍然等于其动量的变化率。之前我们曾经推导出，一队电子从镜面上弹回，施加的压力P=2mv×(nv)。对于相对论性情形，可以写下相同的表达式，但要用p来代替mv。我们还假设电子的速度接近光速，所以可以用c来代替v。最后，我们仍然需要除以6来得到恒星中的压强。这意味着，我们可以将相对论性气体的压强写成P=2p×nc/6=pnc/3。和以前一样，现在可以用海森伯不确定性原理继续推理，认为束缚电子的典型动量是h(n/2)^1/3，所以：

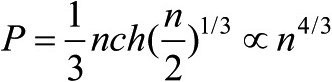
我们又可以把这个近似结果与准确答案相比较，后者是：

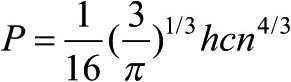
最后，可以用与之前相同的方法，将压强用恒星内部的质量密度来表示，并导出(4)式的替代版本：

P=κ'ρ^4/3

其中κ'∝hc×［Z/(Am_p)］^4/3。和笔者说的一样，压强随密度增加的增长，比非相对论性情形要慢。具体来说，密度的增长指数是4/3，而不是5/3。变化较慢的原因，可以追溯到电子不能以超光速运动的事实。这意味着，我们用于计算压强的“通量”（flux）因子nv，在nc处达到饱和；气体无法以足够的速率将电子送给镜面（或者小立方体表面），以维持ρ^5/3的关系。

我们现在可以来探究这一变化的意义，因为可以通过与非相对论性情形相同的论证来导出与(5)式相应的关系：

κ'M^4/3∝GM²

这是一个非常重要的结果，因为与(5)式不同，它完全不依赖于恒星的半径。这个方程告诉我们，这种挤满了光速电子的恒星，其质量只能有一个非常特殊的值。将上一段中的κ'代入，我们得到的预言是：

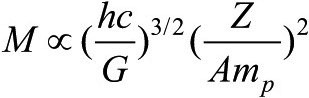
这个结果正是笔者在本章一开始就宣传过的、白矮星可能具有的最大质量。我们已经非常接近于重现钱德拉塞卡的结果了。剩下要理解的部分就是，这个特殊的值为何是可能的最大质量。

我们已经知道，对于质量不太大的白矮星，其半径不会太小，电子不被过度挤压。因此这些电子的量子抖动不会过大，其速度与光速相比也很小。对于这些恒星，我们已经看到，其质量-半径关系是稳定的，形式为RM^1/3=常数。现在想象一下，给恒星增加质量。质量-半径关系告诉我们，恒星会收缩，因此电子被压缩得更厉害，而抖动得更快。再增添更多的质量，恒星就会收缩得更多。因此，增加质量会使电子速度增加，直到最后，它们的速度与光速相当。同时，压强将从P∝ρ^5/3缓慢变成P∝ρ^4/3；而对于后者，恒星只在一个特定的质量上稳定。如果质量增加得超过了这个特定值，那么κ'M^4/3∝GM²的正比符号右侧就会变得比左侧更大，方程就不相等了。这意味着电子压力（位于方程左侧）不足以平衡向内拉的引力（位于右侧），而恒星必然坍缩。

如果更仔细地处理电子动量，并花费心思用高等数学来计算出缺失的数字（对于个人电脑又是一项小任务），我们就能对白矮星的最大质量做出精确的预测。这就是：

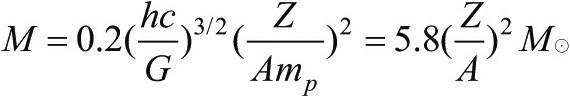
其中用太阳质量（M_⊙）来重新表达了那捆物理常数。顺便注意一下，那些我们没做的所有的额外艰苦工作，仅仅给出了一个比例系数，值是0.2。这个式子给出了我们所追寻的钱德拉塞卡极限：对于Z/A=1/2，这是1.4个太阳质量。

这里真的是我们旅程的终点了。本章的计算，在数学要求上比本书其余部分要高；但在笔者看来，它是现代物理学威力的最壮美的展示之一。可以确定，这不是一件“有用”的事，但一定是人类一次伟大的凯旋。我们利用相对论、量子力学和缜密的数学推理正确地计算出不相容原理与引力对抗所能支撑起的物质球的最大尺寸。这意味着科学是对的；量子力学看起来无论有多奇怪，都是描述真实世界的一套理论。而在这里结束还不错。

[258]又称电浆。

[259]较轻的原子核聚变会放出能量，而较重的原子核聚变会吸收能量。

[260]回忆第五章中，动量确定的粒子其实是由一列无穷长的波来描述；如果允许波长有一定的展宽，就可以开始局域化粒子。但这只能走到这一步；谈论具有确定波长并局域至比这个波长还小的尺度内的粒子是没有意义的。（原书注）

[261]列夫·朗道，1908年生于今天的阿塞拜疆巴库，1968年卒于今天的俄罗斯莫斯科，苏联理论物理学家。下面引用的论文以英文发表于1932年《苏联物理学期刊》第1卷第285页。

[262]詹姆斯·查德威克，1891年生于英国波林顿，1974年卒于剑桥，英国物理学家。

[263]沃尔特·巴德，1893年生于今属德国北莱茵—威斯特伐利亚州的施勒廷豪森，1960年卒于哥廷根，德国籍天文学家。

[264]弗里茨·兹威基，1898年生于今天的保加利亚瓦尔纳，1974年卒于美国加州帕萨迪纳，瑞士籍天文学家。下面引用的论文发表于1933年的《物理学评论》第46卷第76页。

[265]是一种剧烈及明亮的恒星爆炸，发生于大质量恒星的演化末期，或发生失控核反应的白矮星或中子星。

[266]安东尼·休伊士，1924年生于英国弗维宜，英国射电天文学家。

[267]塞缪尔·奥科耶，1939年生于今天的尼日利亚阿比亚州乌穆阿希亚，2009年卒于英国伦敦，尼日利亚籍英籍射电天文学家。下面引用的是发表于1965年《自然》期刊第207卷第59页的论文。

[268]约瑟夫·什克洛夫斯基，1916年生于今天的乌克兰格卢霍夫，1985年卒于今天的俄罗斯莫斯科，苏联天文学家和天体物理学家。他的相关论文于1967年发表在《天体物理学期刊》第148卷第L1页。

[269]约瑟琳·贝尔，1943年生于北爱尔兰鲁根，英国天体物理学家。她和休伊士等人的相关论文于1968年发表于《自然》期刊第217卷第709页。

[270]脉冲星（pulsar）是具有强磁场的旋转中子星，沿其磁极发出电磁辐射，能在地球上被周期性地探测到。

[271]载于《宋会要》《宋史》等。

[272]位于新墨西哥州北部，在这一时期居住着古普韦布洛人。

[273]在金属内或白矮星中的电子，和其他粒子相互作用很弱，可以近似看成气体。

[274]压强是单位面积上的压力。

[275]卡尔·弗里德里希·高斯，1777年生于今属德国下萨克森州的布伦瑞克，1855年卒于今属下萨克森州的哥廷根，德国数学家、天文学家。

[276]这个结论可以推广到整颗恒星，因为我们并没有规定小立方体的具体位置。（原书注）

[277]当然可以更精确地计算电子的运动，但是需要付出引入更多数学算式的代价。（原书注）

[278]牛顿第二定律可以写作F=dp/dt。对于常数质量，这个式子可以写成更熟悉的形式：F=mdv/dt=ma。（原书注）

[279]这里用到了合并幂的一般法则x^ax^b=x^a+b。（原书注）

[280]近似计算中的系数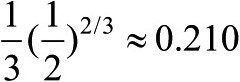，而完整结果中的系数。

[281]在下面的计算中，假设恒星是球对称的，即到球心距离相等的所有位置都是一样的。

[282]对于有数学天赋的人，可以证明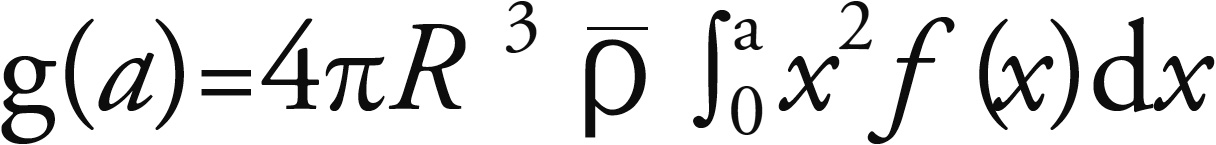，即函数g(a)其实是在我们知道函数f(a)之后才能确定的。（原书注）