在开头几章中，我们建立了理论框架，解释微小粒子是如何四处运动的。它们跳来跳去，毫无偏好地探索广袤的空间，形象地说，在运动中还不忘带着它们的小钟。考虑粒子到达空间中特定位置的可能性，将不同到达方式的小钟加在一起，就会得到一块确定的钟，其大小会告诉我们在“那儿”找到粒子的机会大小。从量子跳跃这种狂野而无序的展示中衍生出了那些日常物体中更为人熟知的性质。从某种意义来说，你体内的每个电子、每个质子和每个中子都在不断地、自由地探索宇宙，只有当计算出所有这些探索的总和后，我们才会得到这样一个世界，幸好你体内的原子能以合理、稳定的排列，保持至少一个世纪。我们还没有完全解决的是粒子之间相互作用的本性。我们还没有具体讨论粒子之间如何交流，尽管已经设法取得了很多进展，特别是利用势的观念后。但什么是势呢？如果世界单单由粒子组成，我们当然可以替换掉“粒子的运动是在其他粒子形成的势中进行的”这样模糊的概念，转而讨论粒子是如何运动和相互作用的。
基础物理学的现代方法称之为量子场论，它为解释粒子到处跳来跳去，补充了一套粒子如何相互作用的新规则。事实证明，这些规则并不比此前见过的规则更复杂；并且，尽管自然世界繁芜庞杂，但现代科学的奇迹之一就是：规则并不太多。“世界永恒的不可理解之处就在于它的可理解性，”阿尔伯特·爱因斯坦写道[183]，“它是可理解的，这本身就是一个奇迹。”
我们先来阐述一下最早被发现的量子场论——量子电动力学，简称QED——的规则。该理论的起源可追溯至1920年代；当时，以狄拉克为代表的物理学家对麦克斯韦电磁场的量子化工作取得了最初的突破。在本书中，你已经多次见到电磁场的量子——光子；但在整个1920和1930年代，这一新理论仍有很多悬而未决的问题。例如，当电子在原子能级间移动时，它究竟是如何发射出光子的？以及，当光子被电子吸收，使电子能跳至更高能级时，光子到底怎么样了？显然，在原子内的过程中，光子是可以被产生和消灭的；而这种事情的机制，本书的“旧”量子理论中至此还没有涉及。
科学史上曾有过屈指可数的几次华山论剑，这些会议看似确实改变了科学的发展方向。如果考虑到与会者通常已经对其课题进行了多年的研究，这些会议也许并没有改变发展方向；但和它们中的大部分比起来，1947年6月在纽约长岛一角举行的谢尔特岛会议更有资格被认为促成了一些特别的事情。光是与会名单就值得列举，因为它虽然短，却是20世纪美国物理学巨擘们的大点兵。按姓名字母顺序：汉斯·贝特[184]（Hans Bethe）、戴维·玻姆[185]（David Bohm）、格雷戈里·布莱特[186]（Gregory Breit）、卡尔·达罗[187]（Karl Darrow）、赫尔曼·费什巴赫[188]（Herman Feshbach）、理查德·费曼、亨德里克·克喇末[189]（Hendrik Kramers）、威利斯·兰姆[190]（Willis Lamb）、邓肯·麦金尼斯[191]（Duncan MacInnes）、罗伯特·马沙克[192]（Robert Marshak）、约翰·冯·诺伊曼[193]（John von Neumann）、阿诺德·诺德西克[194]（Arnold Nordsieck）、朱·罗伯特·奥本海默[195]（J. Robert Oppenheimer）、亚伯拉罕·派斯[196]（Abraham Pais）、莱纳斯·鲍林[197]（Linus Pauling）、伊西多·拉比[198]（Isidor Rabi）、布鲁诺·罗西[199]（Bruno Rossi）、朱利安·施温格[200]（Julian Schwinger）、罗伯特·瑟伯尔[201]（Robert Serber）、爱德华·特勒[202]（Edward Teller）、乔治·乌伦贝克、约翰·哈斯布鲁克·范扶累克[203]（John Hasbrouck van Vleck）、维克托·魏斯科普夫[204]（Victor Weisskopf）以及约翰·阿齐博尔德·惠勒[205]（John Archibald Wheeler）。你已经在本书中见过其中几个名字，而任何一个物理系学生都可能听说过他们中的绝大多数。美国作家戴夫·巴里[206]（Dave Barry）曾经写道：“如果非要用一个词来概括是什么原因导致人类还没有并且永远不可能发挥全部潜能，这个词就是开会。”这无疑是真的，但谢尔特岛会议是个例外。这次会议一开始就报告了后世闻名的“兰姆位移”。威利斯·兰姆利用二战期间发展出的高精度微波技术，发现氢原子光谱实际上不能被旧量子力学完美描述。在观察到的能级中有一个微小的位移，不能用我们本书已出现的理论来解释。这效应极其微小，但对这群聚在一起的理论学者们来说它是一个奇妙的挑战。
我们将在兰姆的报告后淡定地离开谢尔特岛，转而研究在随后数月和数年中出现的理论。过程中会揭示兰姆位移的起源，但是卖个关子，这里先给出加密版的答案：氢原子中并不只是有质子和电子。
QED是解释带电粒子——如电子——如何相互作用，以及它们如何与光子相互作用的理论。单靠它就能解释除引力和原子核以外的所有自然现象。稍后我们将把注意力转向原子核内的现象，并解释为何原子核能保持稳定；它由一堆带正电的质子和不带电的中子构成，如果没有亚原子核现象，后者会在电排斥作用下瞬间飞散。几乎所有的东西，当然包括你看到的和感知的所有东西，都可以通过QED在最深的层次上被解释。物质、光、电和磁，这些都是QED[207]。
我们先来探索一个在本书中已经反复出现的系统：一个包含单个电子的世界。图4.2“小钟跃动”图上的小圆圈表示电子在某一时刻的可能位置。要推导在以后的某一时刻，在某位置X找到它的可能性，我们的量子规则说，要让电子从每个可能的起点跃至X。每次跳跃都会传递一块钟到X；将这些钟相加，就完成了。
我们下面要做的事情，一开始可能看似有点过度复杂，但当然是有价值的。这将会涉及到一些A、B和T——换言之，我们又要进入花呢外套和粉笔灰的领域了，但不会逗留太久。
如果一个粒子于零时刻从位置A出发并于T时刻到达位置B，我们就可以通过A到B的距离以及时间间隔T，计算出从A出发的钟需要逆时针旋转的圈数，并得到B处的钟。简而言之，我们可以把B处的钟写成C(A,O) P(A,B,T)，其中C(A,0)表示A处在零时刻的初始钟，而P(A,B,T)体现出从A跃至B的旋转和收缩规则[208]。我们把P(A,B,T)称为从A到B的“传播子”（propagator）。一旦知道了从A到B的传播规则，我们就完成了准备，可以算出在X处找到粒子的概率。对于图4.2中的例子，我们有很多起始位置，所以就得把每个位置上的钟都传播到X，并把结果加起来。在我们看似牛刀杀鸡的记号中，最后的钟是：
C(X,T)=C(X,0) P(X1,X,T)+C(X2,0) P(X2,X,T）+C(X3,0) P(X3,X,T)+…
其中X1、X2、X3等标记了粒子在零时刻的所有位置（即图4.2中的小圆圈）。再说清楚一点，C(X3,0) P(X3,X,T)就是说“把零时刻位于X3的钟在T时刻传播到X”。不要被骗了，以为会发生什么取巧的事情。我们所做的，只是把已知的东西用一种花哨的方法简记下来：“考虑零时刻位于X3的钟，算出当粒子从X3出发并在T时刻运动到X时，这块钟需要旋转和收缩的量；并且对所有其他零时刻的钟做相同的事情，最后再把它们用钟相加的法则加起来。”相信你一定会认同这句话有点拗口；而笔者的这种记法，让人生更容易了一点。
我们当然可以把传播子看成是钟旋转和收缩规则的体现。但也可以把它看成是一块钟。为了澄清这条生硬的陈述，想象我们知道电子在T=0时能确定电子位于A处，并且它由一块大小为1、指向12点的钟所描述。可以用第二块钟来描述传播行为，其大小是原始钟需要收缩的量，而时刻为所需的旋转圈数。如果从A到B需要将原始钟缩小5倍，并转过2小时，则传播子P(A，B，T)可以用一个大小为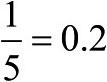
、时刻为10点的钟来表示（即从12点方向往回转动2小时）。B处的钟就是通过将A处的原始钟“乘以”传播子的钟所得到的。
对了解复数的读者多提一句：正如每个C(X1,0)、C(X2,0)可以用复数表示，P(X1,X,T)、P(X2,X,T)也可以，并且前后两者的组合是根据两个复数相乘的数学法则进行的。对于不懂复数的读者这不要紧，因为用钟来描述也同样是准确的。前面两段只是为钟的旋转规则引入了一种稍微不同的思路：可以用另一块钟，来旋转和收缩已有的钟。
我们可以自由设计相乘的规则——即传播子，实现任何结果：将两块钟的大小相乘（1×0.2=0.2），并将两块钟的时间合并，使得第一块钟旋转的量等于12点减10点，这等于2小时。听起来笔者的确用上了屠龙之技，当只用考虑一个粒子时，这些显然没必要。但物理学者都很懒，一般他们不会大费周章，除非从长远来看能省时间。事实证明，当研究包含多个粒子——比如氢原子——的有趣情形时，这些小小的记号对于记录所有的旋转和收缩是非常有用的。
忽略掉细节，在我们计算宇宙某处找到单个粒子的概率时，只有两个关键因素。首先，需要指定钟的初始阵列，这包含了于零时刻在何处可能找到粒子的信息。其次，需要知道传播子P(A,B,T)它本身也是一块钟，包含了粒子从A跃至B的收缩和旋转规则。一旦知道了任意一对起止点的传播子是什么样子，我们就知道了所有的事情，便能很有信心地解出，一种穷极无聊的动力学所对应的宇宙仅包含单个粒子。但其实我们不该如此贬低这个结果，因为把粒子的相互作用加进游戏后，这种简单的状态并没有变复杂很多。所以现在就把相互作用加进来吧。
图10.1：一对电子相互散射的一些方式。电子从左侧出发，在时刻T时，总是到达同一对位置X和Y处。这些图对应了粒子到达X和Y的不同方式。
图10.1形象地说明了所有我们要讨论的关键想法。这是我们第一次接触到费曼图（Feynman diagram），专业粒子物理学者的计算工具。我们的任务是，计算出在某个T时刻，在位置X和Y找到一对电子的概率。开始时，我们被告知电子在零时刻的位置；也就是说，我们被告知了电子的初始钟群是什么样子的。这很重要，因为能够回答这类问题，就等于知道了“在一个包含两个电子的宇宙中会发生些什么”。这听起来可能没什么大进展，但一旦弄清了这个问题，世界就是我们的囊中之物，因为我们会知道大自然的基本构件是如何相互作用的。
为了简化图像，我们只画出了一个空间维度。这完全不会影响结论。先来描述图10.1中一系列图的第一张。 T=0处的小点对应两个电子在零时刻可能的位置。为了方便说明，我们假设上方的电子可以位于三个位置其中之一，而下方的电子可以位于两个位置之一（在现实世界中，必须处理电子可以位于无穷个可能位置的情形，但如果要画出这种情形，会把墨用光的）。上方的电子在稍后某个时刻跃至A，并在那里做一些有趣的事情：它发射出一个光子（用波浪线表示）。这个光子之后跃至B，并在那里被另一个电子吸收。然后，上方电子由A跃至X，而下方电子由B跃至Y。这只是原来那对电子到达位置X和Y的无数种方式中的一种。我们可以把整个过程与一块钟关联起来——称之为“钟1”或者简称C1 。QED的工作就是，告诉我们游戏规则，让我们能推导出这块钟。
在进入细节之前，我们先来描绘出结果。最上方的图代表了最初的一对电子到达X和Y的万千种方式之一。其他的图代表了其他一些方式。这里的关键想法是，对于每一种电子到达X和Y的方式，我们都要确定出一块量子钟，而C1是一长列钟里的第一块[209]。钟尺寸（的平方）告诉我们，在X和Y找到一对电子的概率。因此，我们要再次想象，电子抵达X和Y不只有一条路径，而是通过所有可能的方式相互散射。如果看一下最后几张图，就会看到一些更繁复的电子散射方式。电子不仅交换光子，它们本身就能发射和再吸收光子；在最后两张图中，还发生了非常奇怪的事情。在这些图中，光子看似发射出电子，而电子“绕了一圈”又回到原点；我们稍后会就此展开讨论。目前，我们只需想象一系列愈发复杂的图，描述电子在最终到达X和Y之前如何发射和吸收了大量光子。我们需要想出各种各样让电子到达X和Y的方式，但有两条规则是非常明确的：电子可以从此处跃至彼处，发射或吸收一个光子。这就是全部的规则；电子可以跃动或者分枝。仔细观察就会发现，笔者画出的图中，没有一张违反这两条规则，因为它们从未涉及比两个电子和一个光子更复杂的结点。现在我们必须解释一下如何计算图10.1里每张图对应的钟。
我们来把注意力集中在最上面一张图中，并说明如何确定与之关联的钟（C1）是什么样子。在过程开始时，有两个电子，它们每个都有一块钟。我们会根据钟的乘积法则，将它们相乘得到一块新的单块钟，用符号C表示。它们相乘是有意义的，因为钟实际上编码了概率；而如果有两个独立的概率，则要把它们合在一起就得乘起来。例如，掷两枚硬币，同时得到正面向上的概率是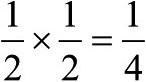
。同样，合并后的钟C告诉我们在两个电子的初始位置找到它们的概率。
剩下就是进行更多钟的乘法。上方电子跃至A，因此有一块钟与之关联；我们叫他P(1,A)（即“粒子1跃至A”）。同时，下方电子跃至B，这也有一块钟，称为P(2,B）。同样，还有两块钟，对应于电子跃至最终位置，把它们记作P(A,X)和P(B,Y)。最后，我们还有一块钟与光子关联，它从A跃至B。由于光子不是电子，光子的传播规则不一定与电子相同，因此我们应该用不同的符号表示它的钟。我们把光子跳跃对应的钟记作L(A,B)[210]。现在，我们简单把所有的钟乘起来，得到一块“主”钟：
R=C×P(1,A)×P(2,B)×P(A,X)×P(B,Y)×L(A,B)
现在我们已经非常接近完成了，还有额外的一些钟收缩需要算上，因为在电子发射或吸收光子时，QED的规则说，要引入一个收缩因子g。在我们的图中，上方的电子发射出光子，而下方电子吸收了它；这就引入了两个g因子，即g2。现在我们真的完成了，最终的“钟1”由C1=g2×R计算得到。
收缩系数g看似有些任意，但它的物理解释非常重要。它显然与电子发射光子的概率有关，而这就编码了电磁力的强度。我们得在计算中引入与现实世界的联系，因为我们计算的是真实的东西；就像牛顿引力常数G承载了引力强度的所有信息，g也承载了电磁力强度的所有信息[211]。
如果我们确实要完成一个完整的计算，现在就要把注意力转向第二张图；它代表了最初那对电子抵达相同目的地X和Y的另一种方式。第二张图和第一张十分相似，电子也从同一位置出发，但现在光子由上方电子在不同的空间位置和时刻发射出来，并被下方电子在不同的位置和时刻吸收。其余的事情和第一张图完全一样，这样我们就得到第二块钟“钟2”，用C2表示。
然后我们继续对每一个可能发射和吸收光子的地方都重复整个过程。还应该考虑到，电子可以从多种不同的可能位置出发。关键在于要考虑到每一种将电子送至X和Y的方式，而每种方式都对应一块钟。一旦我们集齐了所有的钟，就“只需”把它们加起来，产生一块最终的钟，其大小就能告诉我们在X处、Y处分别找到一个电子的概率了。这就完成了我们的任务，搞清楚了两个电子是如何相互作用的，因为我们能做的也只有计算出概率。
刚才所描述的确实就是QED的核心，而大自然中的其他相互作用也能从类似的方式中得到令人满意的描述[212]。笔者很快就会讲到这些，但现在还有其他几点发现要说明。
首先，用一段话来描述两个小而重要的细节。第一：为简化问题，我们忽略了电子因自旋而有两种的事实。不仅如此，光子也有自旋（它们是玻色子），有三种类型[213]。这些只会让计算变得更混乱一点，因为我们所处理的光子和电子的类型，需要跟踪它们每个跃动和分枝阶段。第二个：如果你一直很仔细，则可能已经发现了图10.1中前几张图前面的负号。它们的出现是因为我们是在研究跃至X和Y的全同电子，而带有负号的两张图对应了电子相对于其他图的互换；也就是说，一个电子从上方钟群出发而到达Y，而另一个从较低位置出发的电子到达X。我们在第七章论证过，要合并这些交换的构型，需要先把其中一块钟多转过6小时，因此才会有负号。
你可能已经发现了我们计划中的潜在缺陷——有无数张图共同描述，两个电子如何到达X和Y，而把无数块钟加起来，至少看起来是比较繁琐的。幸好，每次出现光子-电子分枝，都会在计算中引入一个因子g，就能得到缩小的钟的尺寸。这意味着，图愈复杂，它贡献的钟就愈小，而当把所有钟都加起来时，它就愈不重要。对于QED，g是一个相当小的数（大约0.3），所以随着分枝数的增加，钟缩小到了极致[214]。很多时候，只要考虑图10.1中前五张图就足够了，这里的分枝数不超过两个，这样可以省去很多辛勤工作。
对每张费曼图计算钟[215]，把钟加在一起，再对最终的钟求平方得到物理过程发生的概率，这套算法是当代粒子物理学的柴米油盐。但是在我们所说的一切表象之下，隐藏着一个引人深思的问题——它深深困扰着一群物理学者，而其他学者对此毫不在意。
当我们把对应不同费曼图的钟加在一起时，也会允许“量子干涉的狂欢”发生。和双缝干涉实验的情形一样，在那里我们曾须考虑，粒子可以到达荧幕的所有路径，这里我们也须考虑一对粒子从初始位置到达终点所有可能的方式。我们能以此计算出正确的答案，因为它允许不同图之间的干涉。只有当最后所有钟都被加在一起、所有的干涉都被考虑在内时，我们才能求出最后钟大小的平方，计算出物理过程发生的概率。听上去挺简单，但请看看图10.2。
图10.2：观察正在发生之事的人类眼睛。
如果我们试图去确定电子在跃至X和Y时都做了什么，会发生什么呢？我们只有一种方法可以研究这一点，就是根据游戏规则去与体系相互作用。在QED中，这意味着我们必须使用电子-光子的分枝规则，因为没有其他选择。因此，我们与其中一个光子展开相互作用，无所谓它是从这一个或另一个电子发出的。我们用个人版光子探测器——肉眼来探测它。注意，我们现在对理论提出了一个不同的问题：“在X处发现一个电子的同时，在Y处发现另一个，并且我的眼睛能看到一个光子的机会有多大？”我们知道如何得到答案：考虑所有始于两个电子的不同图像，将结束时一个电子抵达X、另一个电子抵达Y且还有一个光子抵达“我的眼中”所相关联的钟都加起来。更精确地说，还得讨论光子如何和肉眼相互作用。虽然这一开始可能很简单，但很快就会失控。例如，光子会与一个位于我眼睛内部原子的电子发生散射，而这会触发一连串的事件，最终导致我意识到眼中有光闪过，也就是说我感知到了光子。因此，要完整地描述所发生的事情就需要明确我大脑中每个粒子的位置，因为是它们在光子到来时会做出反应。我们正在接近一种叫作量子测量问题的东西。
至此，我们已经比较详细地介绍过如何计算量子物理学中的概率。这意味着，如果我们进行某项实验，量子理论允许我们有机会测量得到某些特定结果。只要我们遵守游戏规则，坚持只计算某件事情发生的概率，这个过程就没有任何模糊之处。然而，还是有一些令人不安的地方。想象一位实验者进行一项以“是”或“否”为结果的实验，在实际操作过程中，实验者只会记录“是”或“否”，而不会同时记下两种结果。到目前为止一切还算顺利。
接着再想象第二位实验者在此之后做了些其他的测量（具体内容无所谓）。同样，假设这是一个简单的实验，结果是“咔”或者“不咔”。量子物理学的法则规定，为计算第二项实验结果为“咔”的概率，我们要加起来的钟必须考虑所有可能导致“咔”这个结果的情形。这也可能包括第一个实验者得到“是”以及与之互补得到“否”的两种情形。只有对这两种情形求和后，我们才能得到在第二项实验中测得“咔”的正确的概率。这真的对吗？我们真的得认为，即使在某些测量之后，也应该保持整个世界的相干性[216]吗？还是说，一旦我们在第一项实验中测得了“是”或“否”，则未来就只由那次测量的结果所决定？对后一种做法举例如下：在第二项实验中，如果第一位实验者测得“是”，则第二项实验得到“咔”的概率，就不应该由“是”和“否”的相干求和来计算得到；相反，应该只考虑世界上所有从“第一个实验得出‘是’”演化到“第二个实验得出‘咔’”的方式。这种做法，相比于我们对“是”和“否”的结果求和当然会给出不同的答案；而我们需要知道，想要得到完整的理解，哪种做法才是正确的。
要检查哪种做法才是正确的，就得确定测量过程本身是否有什么特别之处。它是否改变了世界，阻止我们把量子振幅相加，抑或是说，测量的只是可能性恢弘巨网中的一部分，而后者永远保持相干叠加？作为人类，我们可能倾向于认为，现在的某个测量（比如得到“是”或“否”）会不可逆转地改变未来；而如果此事当真，则未来的测量结果永远不可能同时通过“是”和“否”这两条路径。但事情显然并非如此；因为似乎总有机会在未来处于某个量子态的宇宙中找到既通过“是”也通过“否”到达的可能。如果认真接受量子物理学的定律，这些态似乎让我们别无选择，只能通过对“是”和“否”的路径求和，来计算出它们显现的概率。虽然这看起来很诡异，但它并不比在本书中贯穿始终的历史求和更诡异。诡异感只是因为我们非常严肃地对待这些求和观念，乃至在人类及其行为的层面上也准备这样做。从这个角度来看，并不存在什么“测量问题”。只有当我们坚持，测得“是”或“否”的结果确实改变了事物的本质时，我们才会遇到问题；因为这样我们就有责任解释是什么触发了变化、破坏了量子相干性。
我们一直在讨论的量子力学理论方法，反对每当有人（或物）“进行测量”大自然就选择一个特定现实的想法，构成了俗称“多世界”（many worlds）的诠释基础。它非常吸引人，因为它是遵守基本粒子行为定律的产物，并足够严肃地运用这些定律去描述一切现象。但它的含义是惊人的，因为我们得想象宇宙真的是所有可能发生之事的相干叠加，而我们感知到的世界（看起来是具体的现实）之所以如此，是因为我们被愚弄了，误以为每当“测量”某事物相干性就丧失了。换言之，自我意识对世界的感知是受主观加工而成的，因为备选的（可能产生干涉的）历史极有可能无法导出相同的“当下”，这意味着量子干涉可以忽略不计[217]。
如果测量并未真正摧毁量子相干性，那么在某种意义上，我们是在一个巨大的费曼图中度过了一生，而我们倾向于认为确定的事情正在发生，其实是我们对世界粗劣感知的结果。所以说如果在未来某时刻，我们身上发生了一些事情，而这些事情的发生要求我们在过去同时做了两件相反的事情，也并非不可想象的。显然，这种影响只能是微妙的，由于像“得到了工作”和“没得到工作”这样对我们生活影响巨大的事情，很难想象出现一种情形使得无论得不得到工作都能导致相同的未来（记住，我们只能把引出相同结果的振幅加起来）。所以，在这个例子中，得到了和没得到工作，并不会显著地互相干涉，而我们对世界的感知就像是只发生了一件事而没有其他可能一样。然而，两种备选情形的差异愈不明显，事情就愈模糊；如前所述，对于包含少数粒子的相互作用，对其不同可能性求和是完全有必要的。日常生活涉及巨量粒子，这意味着在某个时刻，两种本质不同的原子构型（例如，得到了或是没得到工作）极不可能产生显著的干涉效应，也很难导致未来的情形。反之，这意味着我们可以继续假装认为，世界已经因为一次测量而产生了不可逆的变化，即使实际上并非如此。
但是，在我们真正进行实验时，对于这种计算某事发生概率的严肃事务，这些沉思并不是迫切需要的。对于这些事务，我们知道规则、执行规则，就没有任何问题。但或许有一天，这种欢乐的时光会改变——目前，关于我们的过去可能会如何通过量子干涉影响未来的问题，实验还根本无法涉及。对量子理论所描绘的世界（或多世界）的“真实本质”的沉思，会在多大程度上阻滞科学的进步，这个问题被很好地概括在了“闭嘴计算”物理学派[218]的立场中，它机智地拒绝了任何谈论事物真实性的企图。
回到我们的世界，图10.3展示了两个电子相互散射的另一种方式。一个入射电子从A跃至B，并于此处发射出一个光子，目前还算顺利。但现在电子又顺时至Y，在彼处吸收另外一个光子，再顺时而下，最后可能在C处被探测到。这张图并不违反我们关于跃动与分枝的规则，因为电子完全按照理论规定的方式辐射和吸收光子。按照规则这可以发生，并且如本书标题所示，只要可能都会发生。然而，这种事情似乎的确违反常识，因为我们得接受电子能在时间中逆行回到过去的观念。用这种观念能写出不错的科幻小说，但违反因果律可没法造出宇宙。并且，它看似也会制造量子理论和爱因斯坦狭义相对论之间的直接冲突。
图10.3：反物质……或在时间中逆行的电子。
值得注意的是，正如狄拉克于1928年所意识到的那样，亚原子粒子的这种特殊时间旅行并没有被禁止。如果从“顺时”的角度来重新诠释图10.3中发生的事情，就可以看到一点暗示，一切可能并不像看上去那样有缺陷。在图中，我们得从左向右追踪事件。我们来从时刻T=0开始，那时的世界只有两个电子，位于A和B。我们在这个仅含两个电子的世界中继续，直到时刻T1，这时下方电子发射出一个光子；在时刻T1和T2之间，世界包含两个电子和一个光子。在时刻T2，光子没了，由一个电子（最终到达C）和第二个粒子（最终到达X）所替代。我们不愿将第二个粒子称为电子，因为它是“在时间中逆行的电子”。问题是，从一个顺时间前进的人（比如你）的角度来看，一个在时间中逆行的电子看起来是什么样的？
要回答这个问题，我们来想象，给一个在磁铁附近运动的电子拍摄一些录像片，如图10.4所示。只要电子的速度不太快[219]，它通常会做圆周运动。如前所述，电子可以因磁铁而偏转，这就是老式CRT[220]电视机或者更令人向往的粒子加速器包括大型强子对撞机背后的基本构造理念。现在想象把录像倒放。这就是从我们“顺时”的角度来看“一个在时间中逆行的电子”的样子。我们现在会看到，随着录像播放，“逆时电子”沿相反方向做圆周运动。从物理学者的角度来看，倒放的录像就完全像是另一个正放的录像，其中的粒子和电子几乎完全相同，除了它似乎带正电荷。现在，我们有了问题的答案：逆时电子对我们而言像是“带正电的电子”。因此，如果电子真的能在时间中逆行，则我们可以期待遇到的是“带正电的电子”。
图10.4：一个电子在一块磁铁附近做圆周运动。
这种粒子确实存在，被称为“正电子”（positron）。它们被狄拉克于1931年初引入，来解决他为电子写下的量子力学方程中的问题，可以说这个方程似乎预测了负能量粒子的存在。后来，狄拉克对他的思维方式——特别是对自己数学推导正确性的坚定信念——阐述了绝妙的洞见[221]：“我最终接受了负能态不能从数学理论中被排除掉的事实，所以我想就试着给这些负能态找一个物理解释吧。”
仅仅一年多以后，显然还不知道狄拉克预言的卡尔·安德森[222]（Carl Anderson），在观察宇宙射线（cosmic ray）粒子时，在他的实验仪器中看到了一些奇怪的轨迹。他的结论是[223]：“看似有必要用到一种带正电的粒子，其质量与电子相当。”这再一次说明了数学推理的奇妙力量。为了搞清楚一条数学结论的意义，狄拉克提出了一种新粒子的概念——正电子；几个月后，它就在高能宇宙射线碰撞的产物中被发现了。正电子是科幻小说中常见的元素——反物质。
掌握了这种将逆时间旅行的电子诠释成反物质的方法，我们就可以完成对图10.3的解释了。要说的就是，当光子在T2时刻到达Y时，它分裂成一个电子和一个正电子。两者都顺时而下，直到T3时刻，来自Y处的正电子到达X，在那里它与原来的上方电子融合，产生第二个光子。这个光子传播至T4时刻，并被下方电子吸收。
这听起来可能有点太牵强了：只因为允许粒子在时间中逆行，我们的理论中就得出现反粒子。我们的跃动和分枝规则允许粒子顺时和逆时跃动；尽管我们的偏见可能认为不能允许它们这样做，但我们最后发现，我们不会阻止它们这样做。其实是不能，讽刺的是，如果我们不允许粒子逆时跃动，就会违反因果律。这很奇怪，因为事情看似应该反过来才对。(www.xing528.com)
事情能顺利解决，并不是偶然的；它还暗示了一套更深层的数学结构。其实，当你阅读本章时，可能会感觉到，分枝和跃动规则似乎都比较任意。是否可以制定一些新的分枝规则，并调整跃动规则，来探究这样做的后果？好吧，如果我们这样做，几乎肯定就会造出一个糟糕的理论——比如，一个违反因果律的理论。跃动和分枝规则背后更深层的数学结构，叫作量子场论（QFT）。非凡之处在于，它是建立微小粒子量子理论的唯一方式，并遵守狭义相对论。要使用QFT的工具，跃动和分枝规则就是固定不变的了，我们失去了选择的自由。对于那些追寻基本规律的人来说，这是一个非常重要的结果，因为用“对称性”来去除选择，给人一种宇宙本当“如此”的印象，这给人以理解上的进步之感。在这里用到了“对称性”一词，它是很恰当的，因为爱因斯坦的狭义和广义相对论，可以看成是在对空间和时间结构施加对称性的约束。其他“对称性”进一步约束了跃动和分枝规则，我们会在下一章中与它们简短地相遇。
图10.5：氢原子。
在离开QED之前，还有最后一个坑要填平。如果你还记得谢尔特岛会议的开场报告是有关兰姆位移的，它无法用海森伯和薛定谔的量子理论来解释，是氢原子光谱中的反常（anomaly）现象。会议结束后一周内，汉斯·贝特提出了第一个近似得出答案的计算方法。图10.5展示了以QED的方式理解的氢原子。保持质子和电子结合的电磁相互作用，可以用一系列愈发复杂的费曼图来表示，就像我们在图10.1中看到的两电子相互作用一样。我们在图10.5中画出了最简单的两张图。在QED之前，对电子能级的计算只包含了最上面一张图，它包含了电子陷在由质子产生的势阱中的物理过程。但是，如前面发现的那样，在相互作用中还能发生很多其他的事情。图10.5中的第二张图展示出光子在短暂地涨落（fluctuate）后变成一个电子-正电子对的过程，而它也须包含在电子能级的计算中。这和其他很多图都会作为主要结果[224]的小修正进入到计算中。贝特正确地将“一圈”（one-loop）图——就像图10.5中第二张那样——的重要效应包含了进来，并发现它们会稍微移动能级，从而也稍微改变观测到的光谱细节。他的结果与兰姆的观测一致。换句话说，QED迫使我们把氢原子想象成一个嘶嘶作响的噪声源，亚原子粒子在其中不断诞生和消亡。兰姆位移是人类第一次直接接触到这些空灵的量子涨落。
没过多久，另两位谢尔特岛与会者理查德·费曼和朱利安·施温格就接过了接力棒。几年内，QED就发展成了我们今天所知的样子——量子场论的原型，以及作为范例支撑即将发现用以描绘弱和强相互作用的理论。由于他们的努力，费曼、施温格和日本物理学家朝永振一郎[225]（Sinitiro Tomonaga）获得了1965年诺贝尔奖，“以表彰他们在量子电动力学中的奠基性工作，这对基本粒子物理学产生了深远的影响”。我们下面要讨论的就是这些深远影响。
[183]出自《物理和现实》，于1936年发表于《富兰克林研究所期刊》第221卷第3号第313页；英译版发表于期刊同号第349页。
[184]汉斯·贝特，1906年生于今属法国大东部大区的斯特拉斯堡，2005年卒于美国纽约州伊萨卡，犹太裔德籍美籍物理学家。
[185]戴维·玻姆，1917年生于美国宾州威尔克斯—巴里，1992年卒于英国伦敦，美籍巴西籍英籍物理学家。
[186]格雷戈里·布莱特，1899年生于今属乌克兰尼古拉耶夫州的尼古拉耶夫，1981年卒于美国俄勒冈州塞勒姆，犹太裔美籍物理学家。
[187]卡尔·达罗，1891年生于芝加哥，1982年卒于纽约，美国物理学家。
[188]赫尔曼·费什巴赫，1917年生于纽约，2000年卒于麻省剑桥，美国物理学家。
[189]亨德里克·克喇末，1894年生于荷兰鹿特丹，1952年卒于乌赫斯特海斯特，荷兰物理学家。
[190]威利斯·兰姆，1913年生于加州洛杉矶，2008年卒于亚利桑那州图森，美国物理学家。
[191]邓肯·麦金尼斯，1885年生于犹他州盐湖城，1965年卒于新罕布什尔州汉诺威，美国物理化学家。
[192]罗伯特·马沙克，1916年生于美国纽约，1992年卒于墨西科坎昆，美国物理学家。
[193]约翰·冯·诺伊曼，1903年生于今天的匈牙利布达佩斯，1957年卒于美国华盛顿特区，犹太裔美籍数学家。
[194]阿诺德·诺德西克，1911年生于俄亥俄州马里斯维尔，1971年卒于加州圣巴巴拉，美国理论物理学家。
[195]朱·罗伯特·奥本海默，1904年生于纽约，1967年卒于新泽西州普林斯顿，美国理论物理学家。
[196]亚伯拉罕·派斯，1918年生于荷兰阿姆斯特丹，2000年卒于丹麦哥本哈根，荷兰籍美籍物理学家和科学史学家。
[197]莱纳斯·鲍林，1901年生于俄勒冈州波特兰，1994年卒于加州大苏尔，美国化学家、和平运动人士。
[198]伊西多·拉比，1898年生于今属波兰的雷马努夫，1988年卒于美国纽约，犹太裔美籍物理学家。
[199]布鲁诺·罗西，1905年生于意大利威尼斯，1993年卒于美国麻省剑桥，意大利籍美籍实验物理学家。
[200]朱利安·施温格，1918年生于纽约，1994年卒于洛杉矶，犹太裔美籍理论物理学家。
[201]罗伯特·瑟伯尔，1909年生于费城，1997年卒于纽约，美国物理学家。
[202]爱德华·特勒，1908年生于今天的匈牙利布达佩斯，2003年卒于美国加州斯坦福，犹太裔匈牙利籍美籍理论物理学家。
[203]约翰·哈斯布鲁克·范扶累克，1899年生于康涅狄格州米德尔顿，1980年卒于麻省剑桥，美国物理学家。
[204]维克托·魏斯科普夫，1908年生于今天的奥地利维也纳，2002年卒于美国麻省牛顿，犹太裔奥地利籍美籍理论物理学家。
[205]约翰·阿齐博尔德·惠勒，1911年生于佛罗里达州杰克逊维尔，2008年卒于新泽西州默瑟县，美国理论物理学家。
[206]戴夫·巴里，1947年生于纽约州阿蒙克，美国作家和专栏作家。引文可能出自他于1999年出版的《戴夫·巴里年届五十》一书中第八篇《我在50年中所了解的25件事》。
[207]QED也是常用拉丁文quod erat demonstrandum的缩写，意为“已经证明的，此处为双关，可理解成“物质、光、电和磁都已经通过了量子电动力学的证明”。
[208]为了确保粒子在时刻T在宇宙中某处被找到的总概率为1，传播子也会将钟缩小。（原书注）
[209]我们在之前就遇到过这种想法，当时是在第七章中处理泡利不相容原理。（原书注）
[210]这是一个技术问题，因为贯穿本书的钟的旋转和收缩规则，至此为止，都不包含狭义相对论的效应。如果包含这些效应，就会得出结论，电子和光子的钟的旋转规则是不同的；而要想描述光子，就必须考虑狭义相对论。（原书注）
[211]g与精细结构常数（fine structure constant）有关：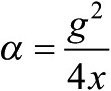
。1910年代，人们对书中前文提到过的氢原子线状光谱做了进一步研究，发现每条谱线实际上是由几条靠得很近的谱线组成的。这被称为精细结构，而这个常数与精细结构有关。它没有单位，数值上约等于1/137。（原书注）
[212]引力的这种描述方式尚未被广泛接受。
[213]在计算过程中出现的“光子”，术语叫作虚光子，有三种类型。而实际能观测到的光子，术语叫作实光子，只有两种。
[214]作者这里忽略掉了一个事实：分枝愈多，图的构型就愈多，这可能会抵消掉钟尺寸减小的影响。这是一个有待解决的科学问题。
[215]术语叫作“振幅”。
[216]coherence。这里是说量子粒子发生干涉的能力。考虑双缝干涉实验，如果在双缝处测量粒子位置，则不能观察到条状干涉图案；如果不在双缝处做测量，则可以观测到干涉图案，而这是由双缝处出发的两列波函数（相干）相加所得出的。这说明，在双缝处所做的测量破坏了系统的相干性，因而荧幕上的波函数不再由双缝发出的两列波函数相加所得到。
[217]这里大概是说，其他历史极不可能演化出相同的“现在”，即是说它们的概率很小，钟的尺寸很小，所以干涉可以忽略；在主观意识中，我们记住了最可能发生的单一历史。
[218]也称为哥本哈根学派。
[219]这是一个技术要求，要保证电子在运动中感受到的磁力强弱大致相同。（原书注）
[220]Cathode ray tube，阴极射线管，又称显像管。
[221]出自收录于查尔斯·维纳编著《二十世纪物理学》（History of Twentieth Century Physics，Academic Press，1977）的狄拉克《忆峥嵘岁月》（Recollections of an Exciting Era）一文第144页。
[222]卡尔·安德森，1905年生于纽约，1991年卒于加州圣马利诺，美国物理学家。
[223]出自《容易探测到的正电荷粒子的显然存在性》，发表于《科学》第76卷（1932年）第1967编第238页。
[224]玻尔早在1913年就预言的结果。（原书注）
[225]朝永振一郎，1906年生于东京，1979年卒于同地，日本物理学家。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
