现在我们已经搭好了理论框架，可以探索量子理论的细节了。其中的核心观念在技术上很简单，但会迫使我们直面对世界的成见，这挺麻烦。之前说过，粒子由遍布的小钟来表示；而钟面上指针的长度（平方）则表示粒子在此处被找到的概率。这些钟并非要点，它们只是数学工具，用于追踪在某处找到粒子的机会。我们还给出了钟面的相加法则，这对描述干涉现象是必不可少的。现在只要再找到一条法则，告诉我们从此刻到下一刻，这些钟会如何变化，就大功告成了。如果说牛顿第一定律告诉我们，当我们不干扰粒子时它会如何行动，那么这条新法则将代替牛顿第一定律。我们现在就从头开始，想象把单个粒子放在一个点。
图4.1：单块钟面，表示粒子确定地位于空间中的某特定点。
我们知道如何表示位于某处的粒子，见图4.1。会有单块钟面放在那里，指针长度为1，因为1的平方是1，意为在那里找到这个粒子的概率是1，或者说百分之百。假设钟的读数是12点，尽管这个选择完全是任意的。只要概率不变，指针可以指向任何方向，但我们必须选取一个起点，那就12点好了。想要回答的问题是：在稍后某时刻，这个粒子位于其他某位置的机会是多少？换句话说，在下一时刻，我们得画多少块钟，还得把它们放在哪里？对于艾萨克·牛顿，这个问题十分笃定；如果在某处放好粒子并不去碰它，它就不会动。但大自然会相当明确地说，这是错的。事实上，牛顿错得不能再错。
正确答案是，粒子在稍后的时刻可以处在宇宙中任何其他位置。这意味着我们可以画无穷多块钟，在空间中每个可能的位置都放一块。这句话值得反复阅读多次，也许笔者得再多说几句。
允许粒子处在任何位置，相当于不对粒子的运动作出任何假设。这是我们能做的最不带成见的事情，而其中也的确有一定的禅定趣味[75]，尽管这似乎违反常识，可能也违背物理定律。
钟表示的是某种确切之物，即一个粒子在钟所在的位置被找到的可能性。如果我们知道，粒子在某时刻位于某特定位置，就用位于那里的一块钟来表示它。前面的提案是说，如果在开始时的零时刻，粒子处在某确切的位置，则在“比零时刻多一点”的时刻，我们得画出大量、应该说是无穷块钟，充满整个宇宙。这是在承认，粒子有可能在一瞬间跃至任意的所有的其他位置。我们的粒子可以同时在一纳米远，以及十亿光年外一个遥远星系中的恒星中央。这听起来，用我们的方言来讲，就是神戳戳的（原文为daft，苏格兰方言）。但要明确的是，理论必须能解释双缝实验；正如脚趾探入静水，会有涟漪扩散，位于某处的电子也须随时间流逝而扩散。我们需要确定的就是，它是如何扩散的。
和水波不同，我们对电子波的提案是，它在一瞬间扩散并充满整个宇宙。从技术上讲，我们会说粒子波传播的规律和水波的传播规律不同，尽管两者都遵循某个“波动方程”。水波的方程不同于粒子波的方程（就是上一章中提到的著名的薛定谔方程），但两者都描绘了波浪形物理。区别在于描述对象从此处传播到彼处的细节。顺带一提，如果你懂一点爱因斯坦的相对论，那么在讨论粒子跃过宇宙时，可能会感到不安，因为这看似在说粒子是比光速还要快的东西。其实，粒子可以在此处，并在瞬间位移到非常远的什么地方，这与爱因斯坦的理论并不矛盾，因为真正的陈述是，信息传播速度不能超过光速，因而量子理论受此约束。正如稍后会了解到，相应于粒子跃过宇宙的动力学，和信息传递完全不同，因为无法事先得知粒子会跳到哪里。我们看似是在构造一个完全无序而混乱的理论，而你可能会想，大自然一定不会如此行事。但是，我们将在本书中看到，日常世界中的秩序，的确是由这种荒谬绝伦的行为中衍生出来的。
如果你不能轻松地接受这个无序的提案——为了描述单个亚原子粒子在下一刻的状态，我们必须用无数块小钟充满整个宇宙，别担心，大多数人都和你一样。在试图揭开量子理论的面纱并诠释它的内在机理的过程中，所有人都困惑不解。尼尔斯·玻尔有句名言写道[76]：“一个人若开始时不为量子理论感到惊骇，他绝不可能理解了它。”理查德·费曼在《费曼物理学讲义》第三卷的引言[77]中也提道：“我想我可以放心地说，没有人懂量子力学。”幸好，按照法则去操作，远比试着去想象这些法则究竟为何意要简单得多。小心翼翼地将一些特定假设及其后果贯彻到底，而不过度思考其哲学蕴涵，是物理学者最重要的技能之一。这完全是传承海森伯的精神：定好初始假设，然后计算推论。如果得到的预言和实际观测一致，则这个理论就可以接受。
很多问题都非常艰深，不能顿悟；而深刻的理解也绝少出现在“尤里卡时刻”[78]。解决之道在于，确保理解每一小步，这样经过足够多步骤，就应该能看到更大的图景。若非如此，我们就会想到，之前的方向不对，必须从头开始。上一章以来的每一小步都不困难；但放下单块钟面，并在下一瞬间把它变成无穷多，这确实是个刁钻的概念，如果想把它们都画出来就更难了。正如伍迪·艾伦所说，永久是很长的一段时间，特别是快到尽头的时候。笔者的建议是，不要惊慌，不要放弃，以及任何时候，无穷都只是细枝末节。下一个任务是建立一套法则，告诉我们在放好粒子后的某时刻，这些钟看起来该是什么样子。
我们探寻的这条法则是量子力学的实质性法则；尽管当考虑宇宙中存在多于一个粒子时，还得加上第二条法则。但是事有先后，现在还是先关注宇宙中只有单个粒子的情形，这样就没人能怪我们猴急。假设在某一瞬间我们知道粒子的确切位置，就可以用一块孤立的钟来表示它。具体的目标是，找到一条规则，告诉我们遍布宇宙的每一块新钟，在未来的任意时刻是什么样子。
我们先不加说明地阐明清楚这条规则。几段之后会说明它们何以如此，但现在我们暂时只把它们当作既定的游戏规则。规则是：假设粒子被放下时是0时刻。在未来的t时刻，一块与初始的钟保持x间距的钟，其指针会逆时针转动正比于x2的角度[79]；这个角度还正比于粒子的质量m，并反比于时刻t。用符号表示，这就是说钟指针逆时针转动的角度正比于mx2/t[80]。换句话说，这意味着粒子质量越大，或者距起始位置越远，其转动角度就越大；而时间间隔越大，转动角度就越小。这是一种算法，也可以说是配方，告诉我们给定一系列钟后，如何算出它们在未来某刻的样子。在宇宙中的每一点，我们都画一块新钟，指针转过的角度按照这条规则得出。这就满足了我们的主张，粒子可以也确实会从初始位置跃至宇宙中其他所有地方，并在此过程中产生新的钟。
为了简化讨论，我们想象在一开始时只有一块钟。当然，有可能在初始时刻已经有很多钟，这表示粒子并不位于一个确切的位置。如何找到处理一大批钟的方法呢？答案是对每一块钟都重复只有一块钟时的操作，并把结果加起来。图4.2展示了这个想法。初始的一系列钟由小圆圈表示，而箭头表示粒子从每个初始的钟跳到位置X，在此过程中“累积”出一块新钟。当然，每个初始的钟都会向X递去一块钟，而我们必须把这所有的钟面加起来，最终确切地构造出位于X的钟。这块钟指针的长度透露出之后在X处找到粒子的概率。
图4.2：钟的跳跃。圆圈代表粒子在某时刻的位置；我们要在每个点上都放一块钟。为计算在X处找到粒子的概率，我们要允许粒子从所有的初始位置跳到那里。箭头代表了这种跳跃中的一部分。线的形状并无含义，当然这也不代表粒子是沿着某条轨迹从初始的钟运动到X。
当粒子能从几个不同位置到达同一点时，我们把钟面加起来，这并不很奇怪。被加起来的每块钟都代表着一种粒子能到达X的不同方式。回顾前面的双缝实验，能更好地理解这里的钟面相加只是为了把对波叠加的描述，用钟面转述出来。可以想象初始的两块钟，每条狭缝处各有一块。在之后的时刻，每块钟都会向荧幕的某个特定位置递去一块钟，而我们得把放下的这两块钟加起来，才能得到干涉条纹[81]。小结一下，计算任意位置的钟的规则就是，用上一章里描述的规则，把所有初始钟逐个在那个位置产生的新钟都加起来。
发明这套钟和指针的语言是用于描述波的传播，同时我们也可以用这些术语来描述更熟悉的波。其实，这些想法历史悠久。荷兰物理学家克里斯蒂安·惠更斯[82]（Christiaan Huygens）早在1690年就对光波的传播做出了类似的著名表述。他并未谈论虚拟的钟，而是强调我们应该把光波中的每一点都看作一个次级波源（就像每一块钟都产生很多次级钟）。这些次级波重叠产生一列新波。这个过程不断重复，因此新波中的每一点也是波源，产生之后的波；后者再重叠，而波就在这种过程中前进。
现在可以回到一个有足够理由困扰你的问题。我们究竟为何选择mx2/t作为钟指针的旋转量？这个量有一个名字，叫作作用量（action）；它有一段悠久而可敬的历史。无人真正理解为何大自然以如此基本的方式运用它，这就是说无人真正能解释为何这些钟会转过这个角度。这就引出了下一个问题：怎么会有人意识到作用量的重要性？德国哲学家和数学家戈特弗里德·莱布尼茨[83]（Gottfried Leibniz）于1669年在一篇未发表的作品里首先提出了作用量，尽管他未能找到在计算中应用它的方法。作用量由法国科学家皮埃尔·路易·莫罗·德·莫佩尔蒂[84]（Pierre-Louis Moreau de Maupertuis）于1744年重新引入，随后被他的朋友，数学家莱昂哈德·欧拉[85]（Leonhard Euler）用于建立一套描述大自然的全新原理，相当有力。想象一个球飞过空中，欧拉发现，该球轨迹上任意两点间的作用量始终小于其他任意轨迹所需的作用量。对于球的例子，作用量与球的动能和势能之差有关[86]。这被称为“最小作用量原理”（principle of least action），可在某些情况下用于替代牛顿第二和第三定律。初看起来，这个原理很古怪，看似球为了以极小化作用量的方式飞行，它需要在抵达某处之前，就得知道它会到那。若非如此，作用量又怎么会在球飞过空中之后被最小化呢？以这种方式表述的最小作用量原理貌似遵循的是目的论：事情是为了实现预定的结果而发生。目的论的想法在科学中名声通常很坏，原因也很明显。在生物学中，复杂生物出现的目的论解释，会等同于支持造物主存在的论证，而达尔文[87]（Charles Darwin）的自然选择进化论，能给出更简单的解释，并且美妙地符合所有数据。在达尔文地理论中，没有目的论的成分：生物体通过随机突变产生变异，而来自环境的外界压力和其他活物共同决定哪些变异会被传给下一代。只靠这个过程，就能形成我们今天在地球上看到的复杂性。换句话说，生物既不需要宏图远谋，也不会日臻完美。与之相反，生物进化是随机行走（random walk），由基因在不断变化的外部环境中不完美地复制所产生。获得诺贝尔奖的法国生物学家雅克·莫诺[88]（Jacques Monod）甚至将“系统性或公理性地否定科学知识可以由显性或隐性地基于目的论原理的理论中得到”称为现代生物学的里程碑。
就物理学而言，对于最小作用量原理是否有效，并无争议；因为它给出的计算结果能正确描述大自然，是物理学的一块基石。只要我们引入费曼的量子力学方法，就可以论证最小作用量原理根本不是目的论的，这些争议就能平息了。飞过空中的球“知道”要选择哪条路径，因为它暗中探索了每一条路径。
钟指针旋转角度规则和作用量的关系是如何被发现的？从历史角度来讲，狄拉克是探索包含作用量的量子理论形式第一人，但他却剑走偏锋，将研究发表在一本苏联期刊中，以示支持苏联科学。以《量子力学中的拉氏量》[89]为题的这篇论文发表于1933年，多年以来蛛网尘封。1941年春，年轻的理查德·费曼已经着手思考，如何用经典力学最小作用量原理导出的拉氏公式发展一套量子理论的新方法。在普林斯顿的一场啤酒派对上，他遇上了赫伯特·杰勒[90]（Herbert Jehle），一位来自欧洲的访问物理学家。像所有物理学者们喝了几杯后都会做的那样，他们开始讨论研究思路。杰勒记得狄拉克的尘封论文，第二天他们就在普林斯顿图书馆里找到了它。费曼立刻开始用狄拉克的理论形式计算。那个下午，就在杰勒的注目下，费曼发现他能从作用量原理中导出薛定谔方程。这是前进的一大步，尽管费曼一开始以为狄拉克一定也已经导出了相同的结果，因为这看起来非常容易；如果你是费曼当然就会觉得容易。费曼后来询问狄拉克，是否知道他1933年的论文只要在数学上多推导几步，就能得到这个结果。据费曼回忆，狄拉克在作完一堂乏善可陈的报告后，躺在普林斯顿的草坪上，简单地答道：“不，我不知道。有点意思。”狄拉克是有史以来最伟大的物理学家之一，但也是个沉默寡言的人。同为最伟大的物理学家之一的尤金·维格纳[91]（Eugene Wigner）评价说：“费曼是第二个狄拉克，只是这次他更接近人类。”
小结：我们阐明了一条规则，使我们能写下完整的一系列钟来表述粒子在某时刻的状态。这条规则有点奇怪：用无穷块钟充满整个宇宙，它们的指针相对旋转量取决于作用量，一个古怪但有历史重要性的量。如果两块或更多块钟落在同一处，就将其相加。这条规则的前提是，必须接受粒子能从宇宙中的任意特定位置，在无穷短的时间内，就跳到其他任何地方。我们在一开始就说过，这些怪异的想法最终必须经受大自然的考验，才能看出是否含有合理的成分。首先，我们来看一个十分具体的例子：海森伯的不确定性原理，作为量子理论的基石之一，是如何从这表面的混乱中衍生出来的。
海森伯的不确定性原理是量子理论中最受误解的部分之一，它是一道门，各种江湖骗子跟杂碎[92]贩子都能通过它编出一套哲学沉思。海森伯的不确定性原理被他发布在1927年的一篇题为《论量子理论运动学与力学之物理内涵》（Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik）的德文论文中。这篇论文的题目很难被翻译成英文。难点在于anschaulich，意思大概是“物理的”或“直观的”。海森伯的动力来源似乎是因为恼火于看到薛定谔的量子理论形式由于更符合直观，而比自己的版本更广为接受，尽管两者能够得出同样的结果。在1926年春，薛定谔确信，他关于波函数的方程，给出了原子内部活动的物理图像。他以为，他的波函数是一种能可视化的东西，跟电荷在原子内的分布有关。后来证实这是不正确的，但它至少让物理学者在1926年的前六个月中感到舒适，直到玻恩引入了他的概率诠释。
在另一方面，海森伯已经基于抽象的数学建立了自己的理论，能极其成功地预言实验结果，但却没有一个清晰的物理来诠释。1926年6月8日，海森伯在写给泡利的一封信中表达了他的烦恼[93]，“关于薛定谔理论的物理部分，我思考得越多就感到越厌恶。关于他理论的Anschaulichkeit[94]，薛定谔写道‘不太可能是恰当的’，我换句话说就是Mist。”德文Mist的翻译是“垃圾”或者“胡扯”……或者“杂碎”。
海森伯决定要做的是，探索“直观图像”或者说是Anschaulichkeit，对于物理学理论应为何种含义。他问自己，量子理论该如何解释关于粒子的常见性质比如位置呢？本着他最初的理论精神，海森伯提议，对于粒子的位置，只有阐明清楚如何测量它，它才有确切的含义。如果不能准确地描述怎么找到，就不能问氢原子中电子在哪。这听起来可能像语言游戏（semantics），但它绝对是有据可循的。海森伯意识到，测量动作本身就会引入扰动，这限制了我们能“认识”电子的程度。具体一点，在他的原始论文中，同时测量粒子的位置和动量时，海森伯估算出了两个测量精确度之间的关系是什么。在他著名的不确定性关系中，海森伯阐述，如果Δx是我们对粒子位置知识的不确定度（希腊字母Δ读作“delta”或“德尔塔”，所以Δx读作“delta x”或“德尔塔艾克斯”），而Δp是对应的动量不确定度，则：
ΔxΔp~h
其中h是普朗克常数，而“~”意为“在数量级上相当”。用文字表达就是，粒子位置和动量的不确定度之乘积，大致等于普朗克常数。这意味着，我们愈是精确地确定粒子位置，对其动量就所知愈少，反之亦然（拉丁文：vice versa）。海森伯得出这个结论，是通过对光子在电子上散射的深入思考。光子是“看到”电子的方式，如同我们看到日常物体，是通过光子散射于其上，并落入我们的眼睛一样。通常，从物体上反弹的光，对物体的扰动难以觉察，但得承认，我们在基本层面上，不能把测量独立于被测物之外。人们可能会烦恼，是否有可能通过设计适当、巧妙的实验，来打破不确定性原理的限制。下面将展示，这是不可能的；而不确定性原理是绝对基本的，因为我们将只用钟的理论来推导它。
不同于先前针对开始于单点位置的单个粒子，我们将考虑“大致知道粒子位置但不知道它究竟在哪”的情形。如果知道一个粒子位于空间中的某个小区域，则我们应该用一群填满该区域的钟来表示它。在区域中的每一个点上都有一块钟，而钟指针长度的平方将会表示在该处找到粒子的概率。如果把钟指针的长度求平方，并把它们都加起来，就会得到1。也就是说，在这块区域中找到粒子的概率是百分之百。
我们过一会儿将用量子规则做一项严肃的计算。不过首先笔者得和盘托出，之前在钟转动规则的部分，未能做一条重要的补充说明。笔者之前没有引入它，因为这是一个技术细节；但如果要计算真正的概率，忽略了它就不会得到正确的答案。这条细节和我们在上一段末尾所说的内容有关。
如果我们从单个粒子所在位置的钟开始，则钟指针长必须是1，因为这个粒子必须以100%的概率能在钟所处的位置被找到。根据我们的量子规则，为了描述从起始位置跳跃之后某时刻的粒子，我们应该将钟传送到宇宙中所有的位置。显然，不能让所有钟指针的长度都保持为1，因为那样我们的概率诠释就崩塌了。举例来说，想象粒子由四块钟描述，对应位于四个不同位置的情形。如果每块钟的大小都是1，则粒子位于四个位置中任一个的概率就是400%，这当然是荒谬的。为了修补这个问题，除了将这些钟顺时针旋转，还须缩小它们。这条“收缩规则”是说，在所有新的钟都产生出来后，每块钟都应该以钟总数的平方根为倍数收缩[95]。对于四块钟的情形，那就是说每条指针都须缩小
倍，也就是说最终每块钟的指针长都是1/2。这样，在四块钟的每一块那里，都有(1/2)2=25%的机会找到这个粒子。用这种简单的方式，我们就能保证，在某处找到粒子的总概率永远是100%。当然，可以有无穷多可能的位置，此时一些钟的大小是零。这可能让人担心，但数学可以处理它。对我们来说，只要想象钟的数量是有限的就够了；并且在所有情形中我们都永远无需知道，一块钟到底收缩了多少。
让我们回到之前的例子中，考虑宇宙中有单个粒子，且不知道其精确的位置。你可以把下面一节当作一个数学小谜题。初次阅读时会感到棘手，也许值得重读一遍；但如果你能够跟上思路，就能明白不确定性原理是如何出现的。简单起见，假设粒子运动于一维，就是说它位于一条直线上某处。更实际的三维情形在本质上没有区别，只是更难画出来罢了。在图4.3中我们绘出了这种情形，用位于一条直线上的三块钟来表示。我们应该想象，钟比这要多得多，在每一个粒子可能处于的位置上都会有一块，但这会非常难画出来。三号钟坐落在初始钟群的最左端，一号钟在最右端。重申一下，这表示的情形是，我们知道粒子从一号到三号钟的中间某处开始运动。牛顿会说，如果我们不去动粒子，则它会停在一号和三号钟之间。但量子规则会说什么呢？这就是乐趣的起点，我们会反复应用钟的规则，来回答这个问题。
图4.3：三块位于一条直线上的钟都指向相同的时间，这描述了一开始位于这些钟所处的区域。我们感兴趣的是，在之后某时刻，在X点处找到粒子的概率。
让我们允许时间滴答前进，并搞明白这一列钟会如何变化。我们会从一个离初始钟群很远的特定位置开始考虑，在图中记为X。后面会对“很远”做更定量的描述，但是现在它就只意味着需要把钟转很多圈。
应用这场游戏的规则，我应该把初始钟群里的每一块钟都移动到X点处，相应地转动指针并收缩指针。在物理上，这对应粒子从初始的一群位置中跃至X点处。每块在直线上的初始钟都给出一块到达X处，所以会有很多钟，我们应该把它们加在一起。求和结束之后，在X处所得到钟指针的长度平方就给出了在X处找到粒子的概率。
现在让我们代入一些数，看看结果如何。比如说，位置X距离钟1的距离是“10”单位，而整个初始钟群有“0.2”单位宽。为了回答一个显而易见的问题“10单位有多远？”，稍后会将普朗克常数引入叙事，但现在我们机巧地回避这个问题，只是简单给出，1单位长度对应钟转过1整圈（12个小时）。这就是说，位置X大约在初始钟群的102=100整圈远处（回忆一下转动规则）。我们还将假设，初始钟群钟的钟大小相同，并且都指向12点。假设它们大小相同，就只是说粒子处于图中位置1和3之间任何位置的概率相同；假设它们读数相同的重要性将适时出现。
要把钟从位置1移动到位置X，根据我们的规则，必须逆时针旋转钟指针整100圈。现在我们来到要比位置1更远0.2单位的位置3，并把那里的钟移动到X。这块钟得经过10.2单位才能到X，所以我们得把它的指针多转一点，也就是10.22，结果很接近104整圈。
现在有两块钟落在X，分别对应粒子从位置1和位置3跃至X的情形，而我们要开始计算最后的钟，就必须把它们加起来。因为它们旋转的圈数都十分接近整数，两块钟都大约指向12点，因此它们相加的结果是一块更大的钟，也指向12点。注意，只有钟指针的最终方向才是重要的。我们不需要追踪它们转过多少圈。到这里都还行，但我们还没完，因为在钟群最左和最右端之间，还有很多小钟。
所以，我们现在把注意力放在左右两端的中点上，也就是位置2。那块钟距离X有10.1单位远，这意味着它将转动10.12圈。这十分接近102整圈——又是整数圈。得把这块钟和位置X上已有的两块钟加起来。同之前类似，这会让位置X处钟的指针更长。再接再厉，在位置1和2之间也有中点，那里的钟跃至X会转过101整圈，这还是会让最终的钟指针更长。但现在重点来了。如果从位置1和上述中点这两个点的中点出发，我们就会得到一块钟，把它移动到位置X时会转过100.5圈。这对应一块指向6点的钟。当我们加上这一块钟时，就会减小位置X处钟指针的长度。你稍加思索就会确信，尽管位置1、2和3产生的钟移动到X后都指向12点，并且尽管1、2和3的中点也产生指向12点的钟，但在位置1、3之间的1/4、3/4处，以及位置2、3之间的这两处，都生成指向6点的钟。总计有五块钟指向上，4块钟指向下。当我们把这些钟加起来时，在X处得到的结果是一块指针很短的钟[96]，因为几乎所有的钟都抵消了。
这种简单考虑下的“钟的抵消”现象，显然可以延伸到实际情况中，即考虑位置1到3之间的所有位置。例如，位置1、3之间的1/8处，会贡献一块示数为9点的钟，而3/8处会贡献一块3点的钟。它们再次彼此抵消。最后的净效应是，粒子从钟群中某处出发并到达X，这样的所有跳跃方式所对应的钟互相抵消。这种抵消展示在图4.3的最右端。箭头表明从初始钟群的各个位置出发并到达X的钟的指针。将这些箭头全部加在一起的净效应是它们全部互相抵消。这就是需要记住的关键信息。
重申一遍，我们刚刚说明了，只要初始的钟群足够大，并且位置X足够远，那么对于每一块到达X并指向12点的钟，都会有另一块钟，到达X时指向6点，从而抵消前者；对于每块到达时指向3点的钟，都会有另一块指向9点的钟到达，并抵消前者，等等。这种全盘抵消意味着，实际上根本没有机会在X处找到粒子。这实在是鼓舞人心又饶有趣味，因为它看起来更像是在描述一个不动的粒子。尽管我们的出发点是一个貌似滑稽的提案，一个粒子从空间中的单点位置出发，可以在短时间后到达宇宙中的任何位置，我们现在发现，如果开始时有一群钟，就不会出现这种滑稽的情况。对于一块钟群，因为钟之间相互干涉的方式，粒子实际上没有机会远离它的初始位置。这个结论，用牛津大学教授詹姆斯·宾尼[97]（James Binney）的话来说，是来自“量子干涉的狂欢”[98]。
为使发生“量子干涉的狂欢”以至于相应的钟抵消，位置X需与初始钟群隔得足够远，以使钟可以旋转很多圈。为什么呢？因为如果位置X太近，那么钟指针不一定有机会转过至少一整圈，这意味着它们不会有效地互相抵消。例如，想象一下，在图4.3中，从位置1的钟到X的距离是0.3而不是10。现在钟群前端的钟在移动后转过的圈数比以前少，对应0.32=0.09圈，这意味着它指向1点多一点[99]。类似地，从钟群后端的位置3出发的钟，现在转过0.52=0.25圈，这意味着它的读数是3点。结果就是，所有到达X的钟都指向1点和3点之间的某个位置，这意味着它们并不相互抵消，反而相加形成一块大钟，指向约2点。所有这些都相当于在说，在靠近原始钟群但在它之外，有合理的机会能找到粒子。笔者说“靠近”的意思是，钟在移动前后，指针的旋转不超过一圈。这就有了一点不确定性原理的味道，但还是有些模糊。所以，我们来探索“足够大”的初始钟群以及“足够远”的位置究竟是什么意思。
我们追随狄拉克和费曼而做出的初始拟设是，描述粒子的钟指针转过的圈数正比于其作用量。对于质量为m、在t时间内跃过距离x的情形，这正比于mx2/t。如果我们想得到具体的数，说“正比于”就不够好。需要知道精确的转动圈数。在第二章中我们讨论过牛顿的引力定律。为了得到定量的预测，我们引入了牛顿引力常数，它决定了引力的强度。有了牛顿引力常数，就可以把数代入方程中，算出具体的结果，比如月球的轨道周期，或者“旅行者2号”航天器在太阳系中旅程的轨道。我们现在需要量子力学中的相似物，一个大自然的常数，能“设定尺度”，让我们对于在特定时间内由初始位置被移过特定距离的粒子，能根据其作用量计算出钟的精确旋转圈数。那个常数就是普朗克常数。
在1900年10月7日一个妙思泉涌的夜晚，马克斯·普朗克设法解释了灼热物体辐射能量的方式。在整个19世纪下半叶，灼热物体的光辐射波长分布与其温度的确切关系，是物理学界的最大谜团之一。所有灼热物体都发射光，且随着温度增加，光的性质也会改变。我们很熟悉彩虹这样的可见波段的光；但光也能以对肉眼来说过长或过短的波长出现，这样人就看不见它们。比红光波长更长的光称之为红外（infra-red）光，可以透过夜视镜看到。波长更长的光对应无线电波。类似地，比蓝光波长更短的光称之为紫外（ultra-violet）光，而最短波长的光一般称为“伽马射线”。室温下，一块未燃烧的煤会发射出光谱（spectrum）中红外部分的光。但如果我们将其投入火堆中，煤块就会开始发出红光。这是因为，随着煤块的温度上升，其辐射光的平均波长减小，最终进入我们肉眼可见的范围。规则是，物体愈热，发射光的波长越短。在19世纪，随着实验测量精度的提升，依然没人知道该用什么样的数学公式来正确地描述这项观测。这个问题常被称为“黑体（black body）问题”，因为物理学者把能完全吸收并发出辐射的理想化物体称为“黑体”。这个问题很严峻，因为它代表着我们无法理解任何或者说是所有物体发出的光的性质。
在普朗克于柏林被任命为理论物理学教授之前的许多年里，他一直在仔细思考这个问题，并将热力学和电磁学领域中的内容联系了起来。普朗克的这个教授职位早前也被提供给了玻尔兹曼[100]（Ludwig Boltzmann）和赫兹，但两人都拒绝了。当时的柏林正是黑体辐射的实验研究中心，普朗克能沉浸于实验工作的核心这实属巧合，而这成了他后来展现的理论物理绝技的关键。当物理学者与同事进行广泛而无计划的谈话时，往往工作成效最佳。
我们非常清楚普朗克获得启示的日期和时刻，因为他和家人在1900年10月7日和他的同事海因里希·鲁本斯[101]（Heinrich Rubens）一起度过了一个下午。在午餐时，他们讨论了当时的理论模型在解释黑体辐射的细节时的失败。到了晚上，普朗克在一张明信片上草草写下一个公式，并寄给了鲁本斯。结果它就是正确的公式，但它也的确十分奇怪。后来据普朗克描述，这是他在尝试过其余所有能想到的方案后的“背水一战”。直到现在也没有人知道普朗克究竟是如何得到他的公式的。在阿尔伯特·爱因斯坦的经典传记《上帝难以捉摸》[102]中，作者亚伯拉罕·派斯[103]（Abraham Pais）写道：“他（普朗克）的推理是疯狂的，但他的疯狂具有神圣的品质，只有最伟大的过渡型人物才能带给科学。”普朗克的提案既费解又具革命性。他发现，只有当假设发射光由大量小能量“包”组成时，他才能解释黑体辐射光谱。换句话说，总能量以一个新的大自然基本常数为单位而量子化，普朗克将其称为“作用量的量子”。今天，我们称其为普朗克常数。
尽管普朗克在当时并未意识到这一点，他的公式其实在暗示，光总是以小包或者说量子的形式被发射和吸收。在现代记号中，这些小包含有能量E=hc/λ，其中λ（读作lambda或兰布达）是光的波长，c是真空中的光速，h是普朗克常数。在这个公式中，普朗克常数是换算因子，将光的波长换算成与之关联的光量子的能量。普朗克认为，光本身由粒子组成，所以辐射光能量是量子化的。而这个最初是由阿尔伯特·爱因斯坦在他创造力井喷的1905年提出的[104]。在这个被称为奇迹年（拉丁文：annus mirabilis）的年份里，他还创造了狭义相对论，以及科学史中最著名的公式，E=mc2。爱因斯坦在1921年由于在光电效应上的工作获得诺贝尔物理学奖（而由于诺奖的神秘规定，他在1922年才获得颁奖[105]），而非更有名的两种相对论。爱因斯坦提议，光可以被看作是粒子流（他在当时没有使用“光子”一词）；他还正确地认识到，每个光子的能量反比于其波长。爱因斯坦的这个猜想是量子理论中最著名的佯谬之一的起源——粒子的行为像波，反之亦然。
普朗克向人们展示，要描述热物体发射的光能，只能假设发射是以量子的形式。这就从麦克斯韦关于光的图像那里挖走了墙脚的第一块砖。最终是爱因斯坦挖空了墙脚，让经典物理学的大厦轰然倒塌。他对光电效应的诠释，不仅要求光以小包发射，还要求它与物质以局域波包的形式相互作用。换句话说，光的行为真的像粒子流一样。
光由粒子组成的，或者说，“电磁场是量子化的”，这种观念极富争议，在爱因斯坦首次提出它的数十年后仍未被接受。爱因斯坦的同僚不愿接受光子的观点，这可以从推荐爱因斯坦加入声名卓著的普鲁士科学院（德文：Preußische Akademie der Wissenschaften）的一份提案中看出来。这份由普朗克本人联署的推荐案完成于1913年，距爱因斯坦引入光子晚了整整八年[106]：
综上所述，在当代物理学如此众多的重大问题中，几乎没有一个是爱因斯坦未曾做出重要贡献的。他在推测中有时也会无的放矢，如他的光量子假说，但这不能过分苛责他；因为若不偶尔勇于冒险，就不能在最精确的自然科学中引入真正的革新。
换句话说，没有人真正相信光子是真实的。人们普遍认为普朗克较为稳妥，因为他的提案更多地涉及物质的性质——发射出光的小振子——而不是光本身更有关联。要相信麦克斯韦的优美波动方程需要被替换成一个粒子理论，实在是太奇怪了。
笔者提及这段历史，部分原因是为了让你相信这些困难是要接受量子理论所必须面对的。难以形象地想象一个东西，比如一个电子或光子，表现得有一点像粒子，又有一点像波，或者谁都不像。爱因斯坦在余生中始终保持着对这些问题的关注。在1951年，也就是去世前四年，他写道：“五十年的沉思没能使我接近这个问题的答案一步：什么是光量子？”
六十年之后，无可辩驳的是，这个我们正在用一系列小钟来构建的理论，能以可靠的精度给出所有用于检验它的实验结果。
那么，这就是引入普朗克常数的历史。但是在我们的目标中，最值得关注的东西，是普朗克常数具有“作用量”的单位；换句话说，它和告诉我们钟要转动多少的量，是同一种东西。它的当代数值是6.6260695729×10－34kg·m2/s，用日常标准来衡量是极小的。这就是我们没有在日常生活中感受到它无处不在效果的原因。
回忆一下前文中，当粒子从一处跃至他处，对应的作用量就是粒子的质量乘以跳跃距离的平方，再除以跳跃发生的时间间隔。这个结果以kg·m2/s单位度量，和普朗克常数一样，所以如果简单将作用量除以普朗克常数，就能抵消所有的单位，得到一个纯数。按照费曼的方法，这个纯数就是我们在考虑粒子从一处跃至他处的情形中，与之关联的钟要转动的角度。例如，如果这个数是1，就是说转动1整圈；如果是1/2，则转动1/2圈，以此类推。用符号表示，在粒子于t时间内跳过x距离的情形中，钟指针转过的精确圈数是
。注意因子1/2出现在了公式中。你既可以认为需要这个因子是为了符合实验，也可以注意到它来自作用量的定义[107]。两者都行。现在我们知道了普朗克常数的数值，就可以真正量化转过的圈数，并且解决前面留下的问题。就是说，跳过“10”单位距离到底是什么意思？
让我们看看，用这个理论处理日常标准中的小物体——一粒沙子，会得到什么。我们发展出的量子力学理论表明，如果把沙粒放在某处，则在之后某时刻，它可以位于宇宙中的任意位置。但这显然不会发生在一粒真实的沙子上。我们已经瞥见了解决这个潜在问题的方法，因为如果钟之间有足够的干涉，对应沙粒从多个不同的初始位置开始跳跃，则它们会互相抵消，使沙子保持静止。我们需要回答的第一个问题是，如果我们把质量等于一粒沙的粒子，在一秒时间内，搬运0.001毫米，钟会转过多少圈？我们不能够用肉眼看到这么小的距离，但对于原子尺度来说它还是相当大的。你可以很容易地将这些数代入费曼的旋转法则中，并算出结果[108]。答案是钟大约得转动一亿年。想象一下这么多圈能产生多少干涉。最终结果是，沙粒留在原处，并且它跳到可辨远处的概率几乎没有，尽管我们真得考虑这粒沙子曾暗中跃至宇宙各处的可能性，这才得到了那个结果。
这个结果十分重要。如果你自己代入数据做计算，就会意识到事情的原因：普朗克常数极小。写出完整形式，它的值是0.00000000000000000000000000000000066260695729kg·m2/s。用任何日常的数除以它，都会得到很大的转动圈数以及很多干涉相消。结果就是，沙粒横跨宇宙的诸次异域之旅完全互相抵消，而在我们的感知中，这位穿越寰宇的旅行者只不过是一粒无趣的沙尘，纹丝不动地躺在沙滩上。
我们特别感兴趣的当然是，钟没有互相抵消的情形。我们已经看到，如果钟的转动不超过一圈，就会发生这样的情形。这种情形下，“量子干涉的狂欢”就不会发生。下面来看看这在定量上意味着什么。
图4.4：现在我们不取定钟群大小、或者到X点的距离的数值，其余和图4.3一样。
我们回到图4.4中画出的钟群，但是这次的分析会更抽象，而不是使用具体的数。我们假设，钟群的大小等于Δx，而X到钟群中最近位置的距离是x。在此情形中，钟群大小Δx对应我们对粒子初始位置认识的不确定性；它从一个大小为Δx的区域出发。我们从点1也就是钟群中离X最近的位置开始，从这个点跃至X，对应的钟的旋转量为
现在我们来考虑最远的点3。把钟从那里移动到X，它会转过更多的量，即：
现在我们可以精确地阐述，钟从钟群中所有点传播到X，并且不抵消的条件：分别从钟1和钟3出发的钟，转动圈数之差应不小于一整圈，即：
W3－W1＜一圈
完整写下来就是：(www.xing528.com)
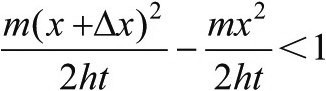
我们现在将考虑特殊情况，其中钟群的大小Δx远小于距离x。这就是说，我们希望粒子跃到远离其初始领域的地方。在这种情形中，从上一个式子中直接推出的钟不完全抵消的条件是：
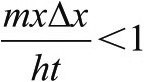
如果你懂一点数学，就能由打开括号项并忽略掉包含(Δx)2的所有项，得到这个结果。这是一个有效的近似，因为之前说过Δx和x相比非常小，而小量的平方是小上加小。
这个式子就是在X处钟不完全抵消的条件。我们知道，如果在某处，钟不完全抵消，则很有可能会在那里找到粒子。因此我们发现，如果粒子在起初位于大小为Δx的钟群中，只要满足上述方程，则在t时间后，在与钟群相距x的较远位置找到粒子的机会不低。此外，这个距离随时间增加，因为它在式子中要除以t。换句话说，随着时间流逝，在距离初始位置更远处找到粒子的机会增加。这看似就像是粒子正在移动。还要注意到，在很远处找到粒子的机会也会随Δx减小（即随初始位置不确定性的减小）而增加。换句话说，我们将粒子固定得愈准确，它从初始位置移开得就愈快。现在这看起来很像是海森伯的不确定性原理。
为了最终达成联系，我们来对方程变形。请注意，对于在t时间内离开钟群到达位置X的粒子，它必须跃过距离x。如果你真的在X处测量到粒子，就会自然得出结论，粒子运动的速度是x/t。还有，要记得质量乘以粒子的速度是其动量，所以mx/t就是测得的粒子动量。现在我们可以继续简化前式，得到：
其中p是动量。这个方程可以变形成：
pΔx＜h
图4.5：一小群随时间扩大的钟，对应一个初始时在局域而随时间前行离域的粒子。
而这个式子真的十分重要，值得进一步讨论，因为它看起来非常像海森伯的不确定性原理。
数学部分暂告一段落，如果你没有用心跟上，应该能从这里重新跟上讨论。
如果一个粒子从一个局域在大小为Δx的斑点内出发，则根据刚刚发现的结果，在一段时间后，粒子可以在大小为x的更大斑点内的任何位置被找到。图4.5描述的正是这种情形。精确地说，这意味着如果我们在刚开始时寻找粒子，则我们在内侧斑点内部找到的机会较大。如果没有测量，而是等一会儿，则稍后能在较大斑点内部某处找到它的机会较大。这就是说，粒子可以从初始的小斑点内的某处移动到较大斑点内的某处。它不一定非得移动不可，仍然有一定概率继续留在尺寸为Δx的较小区域中。但是测量很有可能显示，粒子已经移动到了较大斑点的边缘[109]。如果测量证实了这种极限情形，则我们会得出结论，粒子的动量由我们刚刚导出的式子给出（如果你没有跟上数学推导，只要相信这个结果就好），即p=h/Δx。
现在，我们可以再次从头开始，将一切恢复如初，则粒子再次位于大小为Δx的较小初始斑点中。如果测量粒子，可能发现它位于较大的斑点内部某处，而不是在极限的边缘。我们会得出结论，粒子的动量比极限值小。
想象我们多次重复这个实验，对于开始时位于大小为Δx的小钟群内部的粒子测量其动量，则我们通常会测得动量p的值在零到极限值h/Δx之间。也就是说“如果你重复多次做这项实验，那么我预测，你测得的动量会在零到h/Δx之间”就意味着“粒子动量的不确定度是h/Δx ”。和位置的不确定度类似，物理学者用符号Δp表示这种不确定度，写作ΔpΔx~h。“~”符号表明，位置和速度的不确定度之积大致等于普朗克常数；有可能大一点或者小一点。更细致的数学推导可以得到严格正确的式子。结果会依赖于初始钟群的细节，但没必要为此额外花时间，因为我们所做的已经足够抓住关键思想。
粒子位置的不确定性乘以其动量的不确定性，（近似）等于普朗克常数，这句陈述也许是海森伯不确定性原理的最为人所熟悉的形式。它告诉我们，如果我们知道粒子在某个初始时刻位于某个区域，而在稍后时刻对粒子位置进行测量，就会发现粒子此时的动量值不能比“介于零与h/Δx之间的某个值”更准确地被预测。换句话说，如果我们一开始时，把粒子限制在愈来愈小的区域内，那么它就会有一种趋势，要愈来愈远地跃离这个区域。这一点非常重要，值得再三重申：愈是精确地知道粒子在某个瞬间的位置，就会愈不清楚它的运动快慢，因此也就愈不清楚稍后时刻它会在哪里。
这正是海森伯对不确定原理的陈述。它位于量子理论的核心；但应该要清楚，它本身并不是一条模糊的陈述。它是一条关于我们无法精确追踪粒子的陈述；量子魔法的这种威力并不比牛顿魔法的更大。在前面几页中我们所做的是，从量子物理学的基本规则中推导海森伯不确定性原理；这些规则体现在钟的旋转、收缩和相加里。的确，原理的起源就在于我们的提议认为粒子在测量其位置后，可以位于宇宙中的任何地方。我们最初提出的这条狂野的提议——认为粒子可以处于宇宙中的任何和所有的地方，已经被“量子干涉的狂欢”所驯服；而不确定性原理，在某种意义上，就是起初的无序状态的全部遗存。
在转到下个话题之前，关于如何诠释不确定性原理，笔者还有一些非常重要的事情要说。我们不能犯这种错误，认为粒子实际上位于某个特定的单一位置，而初始钟的传播，其实是反映了我们理解上的某种局限性。如果这样想，就无法正确地利用不确定性原理做计算；因为如果这样想，我们就不会承认，必须要在初始钟群的每一个可能的位置上取一块钟，依次把它们移到一个遥远的位置X，再把它们全部加起来。正是因为执行下面这种做法才给出了我们的结果，即我们必须假设，粒子通过许多可能路线的叠加，才到达了X。我们将在以后的一些实际例子中，用到海森伯的原理。而现在，我们只用到了一些简单的虚钟操作，就推导出了量子理论的关键结论之一，这着实不错。
我们来向式子中插入几个数，更好地感受一下。要等多久，沙粒才能有合理的概率跃出火柴盒？我们假设火柴盒边长为3厘米，而沙粒重1毫克。回忆一下，沙粒有合理的概率跃过给定距离的条件是：
其中Δx是火柴盒的大小。我们来计算，如果想让沙粒跳过x=4厘米，一个超过火柴盒大小的距离，t应该是多少。
透过简单的代数运算可以得到：
代入数据可以得到，t必须大于约1021秒。这是约6×1013年，是宇宙当前年龄的1000多倍。所以这种事情很可能不会发生。量子力学很奇怪，但还没奇怪到可以允许一粒沙子能独立跃出火柴盒的地步。
为了总结本章，以及为进入下一章作准备，我们做最后一次观察。我们对不确定性原理的推导，是基于图4.4中的一组钟的特定构型（configuration）。具体来说，我们安排了初始钟群，使钟指针的大小和指向都相同。这种特殊的安排，对应粒子起初时静止于空间中的特定区域；例如，沙粒静止于火柴盒中。尽管我们发现，粒子很可能不是静止的，我们也发现，对于大物体——沙粒在量子意义上已经是非常大的——这种运动完全检测不到。所以在我们的理论中确实会有某种运动，但是对于足够大的物体，这种运动无法感知。显然我们忽略了一些重要的东西，因为大物体实际上确实在四处移动，并且前面说过量子理论与所有东西都有关，无论大小。我们现在必须解决这个问题：如何解释运动？
[75]或审美趣味，看你的观点。（原书注）
[76]出自海森伯《部分与整体》（Der Teil und das Ganze，英译本标题：Physics and Beyond）一书第17篇《实证主义、形而上学和宗教》（1952）。
[77]这里原著有误，译者没有在《费曼物理学讲义》中找到那句话。从别处找到的出处是《物理世界的本性》（The Character of Physical Law）。
[78]古希腊文εὕρηκα，拉丁文heúrēka，通过神秘灵感获得重大发现的时刻叫作“尤里卡时刻”。
[79]注意，自本章起，钟指针是逆时针转动的；而在上一章中，钟指针随着月相或者波的相位变化，是顺时针转动的。
[80]这个规则还应该给出钟指针的长度。长度的平方正比于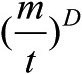
，其中D是粒子运动的维数，见下文。
[81]如果你理解这句话有困难，把“钟”换成“波”试试。（原书注）
[82]克里斯蒂安·惠更斯，1629年生于海牙，1695年卒于同地，荷兰天文学家。
[83]戈特弗里德·莱布尼茨，1646年生于莱比锡，1716年卒于汉诺威，德国哲学家、数学家及启蒙运动家。
[84]皮埃尔·路易·莫罗·德·莫佩尔蒂，1698年生于法国伊勒—维莱讷省圣马洛区的圣茹昂代盖雷特，1759年卒于瑞士巴塞尔，法国数学家。
[85]莱昂哈德·欧拉，1707年生于瑞士巴塞尔，1783年卒于俄国圣彼得堡，瑞士数学家、自然科学家和工程师。
[86]对于质量是m、离地面高度是h的球，其动能等于mv2/2，而势能为mgh。g是所有物体在地球附近自由下落时的加速度。一段运动的作用量，是动能与势能之差，在这段运动两端点之间对时间的积分。（原书注）
[87]查尔斯·达尔文，1809年生于英国什鲁斯伯里，1882年卒于今天的布罗姆利区，英国博物学家。
[88]雅克·莫诺，1910年生于巴黎，1976年卒于戛纳，法国生物学家。
[89]发表于德文的《苏联物理学期刊》第3卷第1期，第64—72页。
[90]赫伯特·杰勒，1907年生于德国斯图加特，1983年卒于德国科布伦茨附近，德籍美籍物理学家。
[91]尤金·维格纳，1902年生于匈牙利布达佩斯，1995年卒于美国新泽西州普林斯顿，匈牙利裔美籍物理学家。
[92]英文维基百科将“肚”（三声）形容为一种来自多种畜养动物胃部的可食用内脏/杂碎；但它在口语中也指废话或胡扯。在这句话中这两种解释都很适当。（原书注）
[93]取自泡利《与玻尔、爱因斯坦、海森伯等人的科学通信：卷1（1919—1929）》中第136篇，Springer出版社。
[94]德文，直观性。
[95]严格来说，将所有的钟收缩相同的倍数，仅当我们忽略爱因斯坦的狭义相对论时，才是正确的。否则，一部分钟会收缩得比其他钟更多。这里我们不用担心。（原书注）
[96]别忘了前文的收缩规则；对于五上四下的情形，结果是一块指向12点、指针长度为原来1/3的钟。
[97]詹姆斯·宾尼，1950年生于伦敦，英国天体物理学家。
[98]“orgy of quantum interference”，语出宾尼于2009年在牛津大学教授的量子力学课程。
[99]1点对应转过圈。
[100]路德维希·玻尔兹曼，1844年生于维也纳，1906年卒于今属意大利的杜伊诺，奥地利物理学家和哲学家。
[101]海因里希·鲁本斯，1865年生于威斯巴登，1922年卒于德国柏林，德国物理学家。
[102]原题为Subtle is the Lord，有方在庆等译的中译本。
[103]亚伯拉罕·派斯，1918年生于荷兰阿姆斯特丹，2000年卒于丹麦哥本哈根，荷兰物理学家和物理史学家。
[104]在论文《关于光的产生和转变的一个启发性观点》中，发表在德文《物理年鉴》第322卷第6号第132—148页。
[105]在诺贝尔奖官网上可以查到，1921年时没有提名者达到获奖条件；诺贝尔基金会依照章程，将当年奖项保留至次年。
[106]德文原文可在S. Grundmann, Einsteins Akte, Springer, 2004一书中找到。
[107]对于质量为m、在t时间内跃过x距离的粒子，如果粒子做匀速直线运动，则作用量为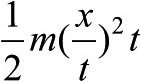
。但这并不意味着量子粒子在从此到彼的运动中走直线。钟的旋转法是这样获得的：将两点间粒子可能通过的每一条路径都关联上一块钟，并把它们加起来。最后能得到这个简单的结果，纯属巧合。例如，如果引入修正，使之与爱因斯坦的狭义相对论一致，那么钟的旋转法则就不这么简单了。（原书注）
[108]一粒沙的典型质量是约1微克，就是一千克的十亿分之一。（原书注）
[109]粒子甚至有机会，移动到比图中大斑点标处的“极限”更远的地方。但我们已经说明，这种情形下的钟趋于抵消。（原书注）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
