量子粒子的奇特特点及电子的运动路径

我们使用的量子理论方法是由理查德·费曼^[48]（Richard Feynman）开创的，他出生在纽约，获得过诺贝尔奖，还会演奏邦哥鼓^[49]。他的朋友兼同事——弗里曼·戴森^[50]（Freeman Dyson）称他“一半是天才，另一半是小丑”。戴森后来改变了他的观点：更准确地说，费曼应该是“彻底的天才，也是彻底的小丑”。我们将在本书中采用费曼的方法，因为它不仅好玩，也可能是理解量子宇宙最简单的方法。

理查德·费曼不仅创造了量子力学的最简单形式，也是一位伟大的老师。他能将其深刻见解带入讲堂或写进书里，并且做到前所未有的清晰，让读者几乎不会困惑。费曼对于那些希望把物理搞得高深莫测的人嗤之以鼻。即便如此，费曼感到还是有必要开诚布公地说明量子理论违反直觉的特点。在他的大学经典系列教材《费曼物理学讲义》^[51]的开头，他写道^[52]，亚原子粒子的行为“既不像波，又不像粒子，也不像云雾或弹子球，或者悬于弹簧的重物，总之不像我们曾见过的任何东西”。下面我们将建立模型，来看看这些粒子的行为究竟如何。

作为研究的起点，我们将假设大自然的基本组成单位是粒子。能证明这一点的不仅有电子总是到达荧幕上特定位置的“双缝实验”，还有其他一系列的实验。“粒子物理”（particle physics）的确不是浪得虚名。我们要处理的问题是，粒子如何运动？当然，最简单的假设就是它们遵循牛顿定律，要么走直线，要么因受力而走曲线。然而这并不正确，因为所有对双缝实验的解释都要求电子必须在通过狭缝时“与自己干涉”，这就意味着电子必须存在着某种扩散。因此我们的挑战就是：建立一套点状粒子的理论，同时也能解释这些粒子的扩散。这没有听上去那么难：只要我们让任意单个粒子都可以同时出现在多个地方，这件事就能成立。当然，这个想法听上去还是不可能的，但单个粒子可以同时身处多地，这本身就是一个相当清晰的表述，即便听起来有些蠢。从现在起，我们将把这些违反直觉、呈点状且能扩散的粒子称为量子粒子（quantum particles）。

接受这个“单个粒子可以同时身处多地”的提案，我们将远离日常经验，进入未知领域。想要理解量子物理，主要障碍之一就是思维造成的困惑。要避免困惑，我们应该效仿海森伯，学会接受、适应与实际经验相悖的世界观。学习量子物理的学生往往不断尝试以日常用语去理解其中发生的事情，常常将感到“不适”和感到“困惑”相混淆。真正引起困惑的正是这种对新观念的抗拒，而不是观念本身固有的难度，因为真实世界并不按人们的日常经验运作。因此，我们必须兼收并蓄，保持开放的思想，不为其古怪而苦恼。莎翁^[53]就深谙此道，他笔下的哈姆雷特^[54]（Hamlet）说^[55]：“那么你还是用见怪不怪的态度对待它吧。霍拉旭^[56]，天地之间有许多事情，是科学所没有梦想到的呢。”

仔细考察水波版的双缝实验，会对着手理解量子物理很有帮助。我们的目标是搞清楚，波的何种特点会产生干涉图案。之后得确保，我们的量子粒子理论得包含这种特点，这样才有可能解释电子的双缝实验。

穿过双缝的波能与自己干涉，有两个原因。一是这列波同时穿过双缝，产生两列新波，继续前进并混在一起。显然，这是一列波可以做到的。不难想象：一列长长的海波，煎盐叠雪地滚向海岸，最后拍打在沙滩上。它是一堵水墙，一种延展而前进的东西。因此，我们需要决定如何把量子粒子描绘成“延展而前进的东西”。第二个原因是，两列来自狭缝的新波在混合时能相长或者相消。显然，两列波这种互相干涉的特点是解释干涉图案的关键所在。一种极端情况是，一列波的波峰和另一列波的波谷重合，这时它们就几乎抵消。因此，我们也得让量子粒子能和它自己进行某种干涉。

图3.1：波是如何描绘电子从源运动到荧幕，以及如何被诠释为代表了电子前进路径的所有可能。从A到C再到E，以及从B到D再到F，是单个电子可能采取的无穷条路径中的两种可能。

双缝实验建立了电子和波之间的关联，让我们看看我们能把这种关联建立得有多紧密。看看图3.1，暂时忽略掉A到E、B到F的连线，重点关注波浪。现在这张图描绘了一只水缸，而从左到右的波浪线就代表在水缸中翻滚的水波。想象一下，就在一块厚木板从水缸的左侧插入平静的水面，形成一股波浪时，我们拍下一张相片。此时得到的快照会显示出一列新形成的波从图片的顶部延伸到底部，而水缸其他位置的水面则保持静止。稍晚拍摄的第二张快照会显示出水波向狭缝移动，而波后面的水面保持平静。再过一会儿，水波穿过双缝，便生成了上述图中右边的条状干涉图案。

现在我们把上一段文字再读一遍，并将“水波”都换成“电子波”，先不管这是什么意思。如果诠释得当的话，实验中如水波般翻滚的电子波，就有可能给我们希望理解的条状干涉图案一个解释。但还需要解释电子逐个击中荧幕后所形成的图案为何是由小点组成的。乍一看，这似乎与波的平滑性有冲突，但其实不然。高妙之处在于，如果我们不把电子波诠释成实际的物质分布（这正是水波的情形），而只是某种信息告知我们这个电子可能所处的位置，就能解释得通了。注意我们说的是“这个”电子，因为这列波描述的是单个电子的行为，这样才可能解释荧幕上点的由来。不要陷入误区，这是描述一个电子的波，而非由许多电子组成的一个波。如果我们想象一下这列波在某时刻的快照，则波浪的最高处就可以被诠释为电子最可能被找到的地方，而最低处就是电子最不可能被找到之处。当这列波最终到达荧幕时，荧幕上会闪现小点，告诉我们电子的位置。电子波唯一的作用，就是让我们能计算电子击中荧幕某特定位置的概率。如果不关心电子波到底“是”什么，则一切看起来都很直截了当，因为只要了解波的样子，我们就能知道电子可能在的位置。但当我们试图理解这个关于电子波的提案对于电子从狭缝到荧幕之旅到底有何深意时，好玩的事情就来了。

在开始研究之前，我们或许应该再把上一段读一遍，因为它非常重要。这一段的含义很不直观，并非一目了然。要解释实验中所观察到的干涉图案，“电子波”的提案具备所有必要性质；但它还只是一个对于真相的猜测。作为优秀的物理学者，我们应该去论证这个猜测的结果，看看它们是否真的符合大自然的规律。

回到图3.1，我们提议，在任何时刻，单个电子都由一列像水波那样的波描述。一开始，电子波在狭缝的左侧。这意味着在某种意义上，电子就位于波中的某处。过一会儿，当电子波像水波那样前进至狭缝，电子此时便位于新波中的某处。可以说，电子是“先位于A再运动到C处”，或者它“先位于B再运动到D处”，或者它“先位于A再运动到D处”，等等。先不要细想，等波穿过狭缝到达荧幕，我们再来看看。现在，电子可以在E或者也可能在F处被找到。我们在图中画出的曲线，表示的是电子从源运动到荧幕可能通过的两条路径。它可以从A到C再到E，或者从B到D再到F。以上只是单个电子可能采取的无穷条路径中的两种可能。

关键之处在于，“尽管电子可以尝试每一条路径，但它实际上只走了其中一条”这句话并没有意义。如果说电子实际上只沿一条特定路径，就好比是在水波实验中封住了一条缝，这样并不会产生干涉水纹，也无助于理解电子干涉图案的形成。必须允许波从两边缝都通过，才能产生干涉图案；这意味着，在从源到荧幕的运动中，得允许电子通过所有可能的路径。换句话说，当我们说电子“在波中某处”时，意思其实是，电子同时位于波中所有的位置！这就是我们必须接受的思维方式，因为如果假设电子实际上位于某特定位置，则这列波将不再扩散，水波的类比就失效了；我们也就无法解释干涉图案了。

或许应该再次重读上面的推理过程，因为它启发了下文的大部分内容。这不是在耍花招；我们在讨论的是，要描述一列扩散的波，同时它也是一个点状电子，那么一种实现的可能是，电子在从源到荧幕的运动中，会扫过所有可能的路径。

我们可以从中得到启发：一列电子波，是在描述单个电子以无穷条不同运动路径，从源运动到荧幕。换句话说，“一个电子如何到达荧幕？”的正确回答是，“它运动在无穷条可能的路径上，有一些穿过这条狭缝，另一些穿过那条狭缝”。很明显，“这个”电子并非日常观念中的粒子，因此称之为量子粒子。

在我们决定找到一种描述方式能从不同角度模仿波行为的电子之后，我们需要发展一套更精确的语言来讨论波。首先我们得能描述，水缸中两列波相遇、混合和彼此干涉的现象。为此，得找出更简易的方法来表示每列波峰与波谷的位置。在专业术语中，这叫作相位（phase）。简单来说，“同相”（in phase）有相互加强之意，而“异相”（out of phase）表示相互抵消。“相位”一词也用于描述月球：在其约28天的公转周期中，月球从新月逐渐盈为满月，再逐渐亏回新月，如此循环。英文中phase一词来自希腊文φάσις（拉丁文转写：phásis），意为天象的出现和消失，月亮明面的周期性显现和消失，似乎引出了phase一词在20世纪尤其是在科学中的一种用法，用于形容周期性的东西。这就为我们如何用示意图来表示水波峰谷的位置提供了一条思路。

对照图3.2，我们可以用一块只有一根指针的钟面来表示相位的变化^[57]，这样就能用一周360度来形象地表示各种情形，例如12点、3点、9点方向，以及其间的任意位置^[58]。在月球的例子中，你可以想象一下，用指针指向12点的方向表示新月，1点30分的方向表示眉月^[59]，3点表示上弦月，4点30分表示盈凸月，6点表示满月，以此类推。在这里，我们是用抽象的数来描述具体的东西，也就是用钟面上的钟点来描述月相。在这种描述中，如果画一个指向12点的钟，我们立刻就可以知道它表示新月。尽管前面没有举这个具体的例子，但如果给出一个指向5点的钟，你也会知道月相正在接近满月。用抽象的图像或符号来表示真实的东西，是物理学的基础，这也是物理学者使用数学的根本目的。当能用简单的规则操控抽象的绘景，从而对现实世界做出坚实的预言时，这种方法的力量就体现出来了。一会儿就能看到，钟面就能让我们做出这种预言，因为用它就可以跟踪波峰和波谷的相对位置。反过来这也能让我们计算出不同的波在相遇时是会互相削弱还是增强。

图3.3描绘了两列水波在某时刻的状态。波上每一点都用一块钟来描述。我们用12点表示波峰，6点表示波谷。在波峰和波谷之间的状态，就跟前面的月相一样，也可以用这两个时刻之间的钟点来表示。相邻的波峰或者相邻的波谷的间距是一个重要的量，叫作波的波长。

图3.3中的两列波彼此异相，意味着上面一列波的波峰和下面一列波的波谷对齐，反之亦然。如此，当我们把两列波叠加在一起，它们会互相削弱；如果它们的振幅也相同的话，就能完全抵消。这在图的底部作出了说明，叠加的“波”是一条水平线。用钟的语言来描述的话，就是上面一列波以12点表示的波峰，全都和下一列波以6点表示的波谷对齐了。其实，在任何位置上，上面一列波的钟面指针都与下面一列波的指针完全相反。

图3.3：两列被安排为可以完全抵消的波。上面一列波和下面一列异相，或者说波峰和波谷对齐，并且振幅相同。当两列波相加时，它们完全抵消，结果是没有波。如图片底部所示，“波”成为水平线。

在这个阶段，用钟来描述波，似乎是小题大做了。确实，如果只是想把两列水波加起来，我们只需要把每列波的高度相加，完全不需要钟。对于水波这样说没错，但我们并不是执着于使用工具，引入这些钟自有原因。后面会很快看到，使用钟面来描述特别灵活，对于描述量子粒子是绝对必要的。

记住这条以后，我们现在需要花一点时间，发明一套精确描述钟面读数的相加规则。把规则应用于图3.3的情形中，必须得出相“抵消”的结果，什么都不剩下。诸如12点抵消6点，3点抵消9点等。当然，这种完美抵消是两列波完全异相的特殊情形。我们要找到一套更通用的规则，用于描述任意形状、任意相位的两列波相加的一般规则。

图3.4展示的是另外两列波。这次它们的对齐方式有所不同，一列波与另一列相比，只是相位略有偏置。我们还是用钟标记出了波峰、波谷及其中点。现在，上面一列波的12点与下面一列的3点对齐。接下来我们将要阐明这两列波相加的规则，就是平行移动一块钟的指针，使其头部与另一块钟的指针尾部重合。然后我们画一根新的指针，连接前一根指针的尾部和后一根指针头部，补齐三角形。这个方法的图解在图3.5中。新指针的长度与其他两者不同，并指向不同的方向；它可以放在新的钟面上，用来描述原来的两列波之和。

图3.4：两列稍为偏置的波。上面一列波和中间一列波相加得到底部的波。

现在我们可以更精确地用简单的三角函数来计算任意两块钟相加的结果。在图3.5中，我们把指向12点和3点的两块钟面加起来。假设原来的指针长1cm（对应波峰高为1cm的水波）。当两根指针首尾相接时，我们得到一个等腰直角三角形，腰长1cm。新指针长度就是三角形第三条边的长度，在三角函数中称为弦或斜边（hypotenuse）。根据勾股定理^[60]，斜边的平方等于其他两边的平方和：h²=x²+y²。代入数值得到h²=(1cm)²+(1cm)²=2cm²。因此新指针的长度h就是2的平方根厘米，约1.414cm。那新指针指向什么方向呢？为此，我们需要知道三角形的一个内角，在图中以θ标出。对于这个两根指针等长，且一根指向12点，另一根指向3点的情况，也许你不借助三角函数也能算出来。斜边显然与直角边呈45度角，所以新的“时刻”是12点与3点的中间值，就是1点30分。这个例子是特殊情形，我们选定两块钟，使其指针成直角，并且长度相等，是为了简化计算。但是，这种方法显然是适用于计算出任意两块钟面相加所得的指针长度和钟点数。

图3.5：钟面相加规则。

现在我们再来回顾图3.4。在新一列波的每一点上，我们都可以用刚才的算法，通过求原来的两块钟面之和，得到新钟面的指针长和钟点，继而得知那一处的波高。如果新的钟指向12点，答案很明显，波处于波峰，波高就是指针长。同样当新钟指向6点时，显然波就处于波谷，波的深度也等于指针长。另外如果钟指向3点或者9点时，因为指针垂直于12点方向，则波高为零。要直接计算任意钟点对应的波高，我们需要用指针长h，乘以指针与12点夹角的余弦。例如，3点与12点的夹角是90度，其余弦值为零，因此波高也为零。与之类似，1点30分与12点的夹角是45度，其余弦值为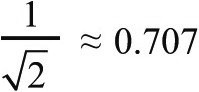，因此波高约为指针长乘以0.707。如果你的三角函数知识不足以理解最后几句，大可以略过，这没有关系。这里重要的原理是：给出指针的长度和方向，就能计算出波高。只要你仔细地画好时钟，用尺子准确地测画出指针在12点方向上的投影，即使你不理解三角函数，也可以近似求解。（笔者明确建议，阅读本书的人不要按照这个方法做，因为学会正弦和余弦是有用的。）

这就是钟面相加的规则。我们反复应用这个规则去计算图3.4中两列波任意对应点之和，结果看起来不错。

图3.6：三块不同的钟，它们在12点方向上投影相同。

在这种对水波的描述中，最重要的就是指针在12点方向的投影，它对应一个数值：波高。看看图3.6里的三块钟。它们都对应相同的波高，它们表示的是相同水波高度的等价方式。这就是为什么在描述水波时，钟其实并不是十分必要。但显然它们是不同的钟，在后面的篇章将会看到，在用它们描述量子粒子时这个区别很大；因为对量子粒子而言，指针长度（或钟的大小）具有非常重要的意义。

在本书的某些地方，描述的事情会相当抽象，特别是目前阶段。为免陷入心烦意乱，我们需要登高望远。戴维孙、革末和汤姆孙实验发现的干涉图案，及其与水波实验的相似性，能启发我们做出拟设：应该用波来表示粒子，而波本身可以用很多钟面来表示。我们能想象电子波“像水波一样”传播，但我们尚未解释电子波到底是如何传播的，甚至水波的传播原理也没有解释。到目前为止，重要的是我们认识到用水波去类比，以及任何时刻的电子都可以用一列波来描述，而这列波可以像水波一样传播和干涉。在下一章我们会有更深入的认识，并且能更精确地表述：随着时间流逝，电子是如何运动的。在此过程中，我们将发现许多宝藏，包括海森伯著名的不确定性原理^[61]（英文Uncertainty Principle）。

在继续了解那些知识之前，希望我们能花一点时间，谈谈将被用于表示电子波的钟。需要强调的是，这些钟绝不是真实的，而它们的指针也和一天中的时刻完全没有关系。用一系列小钟来描述真实物理现象的想法，并不像看上去那么异想天开。物理学者们用类似的技巧来描述大自然中的许多东西，而我们已经见识到如何用一系列小钟来描述水波。

这种抽象技巧的另一例是描述房间内各处的温度，它可以用一系列数来表示。这些数和我们的钟一样，并不作为真正的物理对象而存在。这些数及其在房间中对应的位置，只是便于表示温度的一种方式。物理学者把这种数学结构称为场（field）。温度场只是与每个位置都对应的一系列数。在量子粒子的情形中，场更复杂一些，因为在每个位置需要一块钟，而不只是一个数。这个场通常称为粒子的波函数（wavefunction）。波函数需要一系列钟，而温度场或水波只需要一系列数，这个差异很重要。在物理学术语里，钟的出现是因为波函数是“复数”场，而温度或水波高都是“实数”场。我们不需要这些术语，因为可以用钟面来理解^[62]。

对于温度场能直接感知，而波函数不能这一事实，我们也无需担心。即使我们不能直接摸到、闻到或者看到这个场，也没有关系。说实在的，如果将对宇宙的描述，限制于能够直接感知的事物范围内，我们就无法深入研究物理。

在讨论电子的双缝实验时，我们曾说，电子波的最高处，就是电子最可能所处的位置。这种诠释使我们了解了电子击中荧幕发出的点状闪光是如何组成条纹干涉图案的。但这个描述现在不够精确了。我们希望用一个数来描述在某个特定位置找到电子的概率。这就凸显用钟来表示的必要性，因为我们想要的是概率，并不只是波高。正确的诠释应该是，指针长度的平方表示在该钟所处位置找到粒子的概率。这就是为何要用钟来描述，而不是简单的数，因为前者用起来更灵活。这种诠释并非一目了然，笔者也无法很好地解释它为何是正确的。我们知道它正确，是因为它得出的预测与实验数据一致。对于波函数的这种诠释，是量子理论早期先驱者们面对的棘手问题之一。

波函数（即那些钟）是由奥地利物理学家埃尔温·薛定谔^[63]（Erwin Schrödinge）在其1926年发表的系列论文中引入量子理论的。在他6月21日投稿的论文^[64]中包含了一个方程。这个方程值得每一个物理系本科生铭记在心，它很自然地被称为薛定谔方程：

(www.xing528.com)

希腊字母Ψ^[65]代表波函数，而薛定谔方程描述的就是它如何随时间流逝而变化。这个方程的细节与我们的目标并不相干，因为本书不会使用薛定谔的理论方法。但有意思的是，尽管薛定谔为波函数写下了正确的方程，但在一开始他却没能给出正确的诠释。是马克斯·玻恩^[66]（Max Born），1926年仍在研究量子理论的最年长的物理学者之一，在其43岁高龄之际，仅在薛定谔的论文提交后四天就提交了论文^[67]，其中给出了波函数的正确诠释。在1926年他是当时研究量子理论最年长的物理学者之一，笔者强调这个年龄，是因为在1920年代中期，量子理论被称为“男孩物理学”（德文：Knabenphysik），大多数核心学者都年轻。1925年，海森伯23岁；沃尔夫冈·泡利^[68]（Wolfgang Pauli）22岁^[69]，我们在后面会提到他著名的不相容原理（Exclusion Principle）；而首先正确写出描述电子方程式的保罗·狄拉克^[70]（Paul Dirac）是22岁。人们常说，正是因为这些物理学家还年轻，所以不受传统思维方式的束缚，可以完全接受量子理论所代表的激进的新世界图景。38岁的薛定谔在这支队伍里算得上是老人，而他也的确从未对量子理论感到安心，尽管他本人在该理论发展中举足轻重。

玻恩因其对波函数的激进诠释获得了1954年诺贝尔物理学奖。在他的诠释中，某特定位置处的钟指针长度的平方，就表示在那里找到粒子的概率。例如，如果在某处的钟指针长度是0.1，则平方是0.01。这就是说，在这里找到粒子的概率是0.01，也就是百分之一。你可能会问，为何玻恩不在一开始就将指针的长度平方，这样在上一例中，指针的长度就变成了0.01。这行不通，因为我们在考虑干涉时会把钟面相加；而两个0.1的平方（0.01）求和（得出0.02），与先把0.1和0.1相加，再平方（得出0.04）的结果是不一样的。

还可以用另一个例子来展示“概率诠释”这个量子理论中的重要观念。想象我们去操作一个粒子，并用一系列特定的钟来描述它。再想象我们有一台可以测量粒子位置的设备。这台听起来简单、做起来难的设备可能是一个能快速封闭住空间任何区域的小盒子。如果理论告诉我们，在某处找到粒子的概率是0.01（因为钟的指针长为0.1）的话，那么我们在这个位置周围合上盒子时，在盒子里能找到粒子的概率是百分之一。这意味着在盒子里找到东西的可能性很小。但是，如果我们重置实验，使一切归位，再次用相同的一系列钟来描述这个粒子，我们能不断重复进行这个实验，想重复几次都可以。现在，我们每100次望向盒子，平均都会有1次看到有粒子在里面，而剩下99次里盒子是空的。

用钟指针长度的平方计算在某特定位置找到粒子的概率，这并不让人很难领会，但它的确看起来像是我们（更准确一点说是马克斯·玻恩）凭空捏造的。从历史角度来看，它也确实让很多大科学家接受，包括爱因斯坦和薛定谔。半个世纪后，狄拉克回顾1926年的那个夏天时写道^[71]：“结果发现，找到诠释比得到方程要困难得多。”尽管这很困难，值得一提的是，在1926年末，氢原子辐射的光谱，这个19世纪物理学的最大谜团之一，就分别通过海森伯和薛定谔的方程被计算出来了（狄拉克最后证明了这两种方法在所有情形中都是完全等价的）。

1926年12月4日，爱因斯坦在寄给玻恩的一封信中写下了他反对量子力学概率性的名句：“这个理论说了很多，但并未引领我们更接近他老人家的奥秘所在。无论如何，我确信，他老人家不掷骰子（德文：Der Alte würfelt nicht.）。”问题是在此之前，人们都假设物理学是完全确定性的。当然，概率不只在量子理论中存在，使用它的场景从赌马到热力学，多种多样。别忘了，热力学是整个维多利亚时代^[72]工程学的基础。但是，我们在这些情形中使用概率，是因为缺乏对研究对象的了解，而不是因为某种基本性质。想想掷一枚硬币——赌博的雏形。我们对概率在这种场合的应用都很熟悉。如果掷硬币100次，我们预想的是，平均有50次是正面朝上，50次反面朝上。在量子理论出现之前，我们必须得说，如果知道了关于这枚硬币的一切——包括掷向空中的具体方式、重力吸引、拂过房间的微风、空气温度等等——则我们在原则上就可以算出，硬币是会正面还是反面向上落地。因此，概率在这种场合中的出现，反映出的是我们对所研究体系的无知，而不是体系本身的内在性质。

而量子理论中所说的概率则完全不同，它是基本性质之一。我们只能预测粒子处于此处或彼处的概率，不是因为我们无知。即使在原则上，我们都无法预测粒子的位置会在何处。如果我们去找的话，我们能完全精确地预测的只是粒子在某特定位置被找到的概率，及这个概率如何随时间而变化。1926年，玻恩优美地表达了这一点^[73]：“粒子之运动遵循概率法则，而概率本身则按因果律传播。”这正是薛定谔方程的作用：只要给定了它在过去的样子，用这个方程就能计算出波函数在未来的样子。就此而言，薛定谔方程类似于牛顿诸条定律。不同的是，用牛顿诸条定律能计算出粒子在未来任意时刻的位置和速度，而用量子力学只能计算出粒子在某特定位置被找到的概率^[74]。

这种预测能力的丧失，曾困扰了爱因斯坦和他的很多同行。得益于八十多年来的后见之明，和在此期间研究者们大量艰苦的工作，这些争论现在看来有些多余。我们很容易就能总结道，玻恩、海森伯、泡利、狄拉克等人是对的，而爱因斯坦、薛定谔等“老卫兵”是错的。但在那个时候，当然有可能怀疑量子理论在某些方面并不完备，而概率的出现是因为我们忽略了粒子的某些信息，正如在热力学或掷硬币中那样。今天，这种想法便罕有认同了。理论和实验的进展指出，大自然确实使用随机数；而在预言粒子位置方面丧失确定性，是物理世界的一种内在性质。计算出它出现的概率是我们能做到的极限。

[48]理查德·费曼，姓氏或译费恩曼，1918年生于纽约，1988年卒于洛杉矶，美国理论物理学家。

[49]Bongos，一种拉美双鼓。

[50]弗里曼·戴森，1923年生于英国伯克郡克罗索恩，2020年卒于美国新泽西州普林斯顿，英裔美籍理论物理学家和数学家。

[51]The Feynman Lectures on Physics，电子版见https://www.feynmanlectures.caltech.edu/

[52]译文出自第三卷第一章《量子行为》第一节《原子力学》，译文参考了潘笃武、李洪芳的中译本，上海科学技术出版社出版。

[53]威廉·莎士比亚，1564年生于沃里克郡埃文河畔斯特拉特福，1616年卒于同地，英格兰戏剧家和诗人。

[54]哈姆雷特，莎士比亚同名作品中的主要角色之一，丹麦王子。

[55]本段取自第一幕第五场末尾；中译文取自朱生豪译本。

[56]Horatio，莎士比亚《哈姆雷特》中的主要角色之一，哈姆雷特的好友。

[57]后面会看到，指针的长度还代表振幅。

[58]在本章中，钟指针随着月相或者波的相位变化，是顺时针转动的；而在下一章和以后，钟指针是逆时针转动的。

[59]注意图3.2中这些是逆时针方向标注的，而钟面上是顺时针。

[60]在外国通常称为毕达哥拉斯（希腊文Πυθαγόρας，拉丁文转写：Pythagóras）定理。

[61]不确定性原理（英文：Uncertainty Principle；在当代德文中叫作Unschär-ferelation），直译是模糊关系。

[62]对于熟悉数学的读者，可以如此替换词汇：“钟”换成“复数”，“钟的大小”换成“复数的模长（modulus）”，“指针的方向”换成“相位”。（原书注）

[63]埃尔温·薛定谔，1887年生于奥地利维也纳，1961年卒于同地，奥地利籍爱尔兰籍理论物理学家。

[64]指题为《作为特征值问题的量子化》的四篇论文中的最后一篇，发表于德文《物理年鉴》第386卷第18期第109—139页。

[65]拉丁文转写：Psi，中文音译普西。

[66]马克斯·玻恩，1882年生于今属波兰的弗罗茨瓦夫，1970年卒于哥廷根，德国理论物理学家和数学家。

[67]指题为《论碰撞过程的量子力学》的两篇论文中的第一篇，发表于《物理学期刊》第37卷第863—867页。

[68]沃尔夫冈·泡利，1900年生于维也纳，1958年卒于苏黎世，奥地利籍理论物理学家。

[69]原文有笔误，此时应为25岁。

[70]保罗·狄拉克，1902年生于英格兰布里斯托尔，1984年卒于美国佛罗里达州塔拉哈西，英籍理论物理学家。

[71]出自《相对论性电子波动方程》，于1977年7月4—9日期间发表在匈牙利科学院物理中心研究所举办的欧洲粒子物理大会上。

[72]英国维多利亚女王统治时期（1837—1901），其中英国开始了第二次工业革命。

[73]出自题为《论碰撞过程的量子力学》的两篇论文中的第二篇，发表于《物理学期刊》第38卷第803—827页。

[74]也能计算出粒子被测得某特定速度的概率。