三角高程测量原理-建筑工程测量技巧

三角高程测量是根据已知点高程及两点间的竖直角和距离，通过应用三角公式计算两点间的高差，求出未知的高程。

如图3.32所示，已知A点的高程为HA，测定B点的HB。图中：D为A，B两点间的水平距离，α为在A点观测B点时的垂直角，i为测站点的仪器高，v为棱镜高（目标高），HA为A点高程，HB为B点高程，V为全站仪望远镜和棱镜之间的高差，V=D tanα。

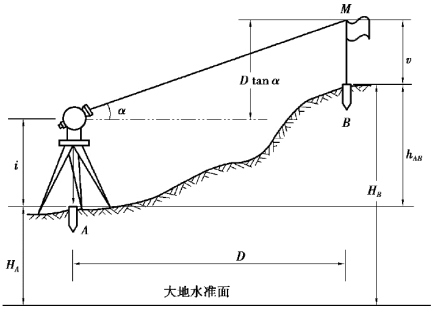
图3.32　三角高程测量原理图

为了确定高差hAB，可在A点架设全站仪，在B点竖立棱镜杆，观测垂直角α，并直接量取仪器高i和棱镜高v，若A，B两点间的水平距离为D，则根据图3.32可知：

故

若用全站仪测得斜距S，则高差计算公式为：

三角高程测量一般要进行往、返观测，即由A向B观测称为直觇，再由B向A观测称为反觇，这种测量称为对向观测。

如果A，B两点相距不太远，可以将大地水准面看成水准面，也不用考虑大气折光的影响。但对于较远的距离，则水准面及大地水准面均是曲面这一点不容忽视，因而对于长距离的三角高程测量，应进行地球曲率改正，简称球差改正（f1），如图3.33所示。

式中，R为平均地球曲率半径，取6 371 km。(www.xing528.com)

由于地球曲率影响总是使测得的高差小于实际高差，因此，球差改正f1恒为正值。

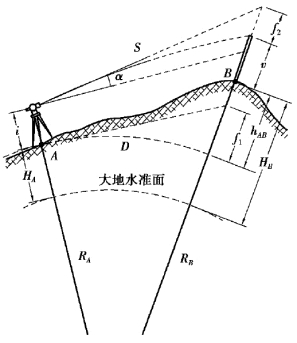
图3.33　三角高程测量的地球曲率与大气折光影响

另外，由于围绕地球的大气层受重力影响，低层空气的密度大于高层空气的密度，观测垂直角时的视线穿过密度不均匀的介质，成为一条向上凸的曲线（称为大气垂直折光），使视线的切线方向向上抬高，测得垂直角偏大，如图3.33所示。因此，还应该进行大气折光影响的改正，简称气差改正（f2），其恒为负值。

大气垂直折光使视线成为曲率大约为地球表面曲率的1/k倍的圆曲线（k称为大气垂直折光系数），因此，可得到气差改正的计算公式：

球差改正和气差改正加在一起，称为两差改正（f）：

大气垂直折光系数k随着时间、日照、气温、气压、视线高度和地面情况等因素而改变，一般取其平均值，令k=0.14。

注意：两差改正计算公式中D的单位为米，R的单位为千米，f的单位为毫米。

考虑两差改正，三角高程测量的高差计算公式为：

由于折光系数的不确定性，使两差改正值也具有误差，若能在短时间内在两点间进行对向观测，并取其平均值，则由于k值在短时间内不会改变，而高差hBA必须反号与hAB取平均，两差改正得到抵消。因此，对要求较高的三角高程测量，应进行对向观测。