建筑工程测量：偶然误差统计特性

偶然误差从表面上看没有任何规律性，但是随着对同一量观测次数的增加，大量的偶然误差就表现出一定的统计规律性，观测次数越多，这种规律性越明显。

我们以某测区在相同观测条件下进行的358个三角形内角观测为例，来分析偶然误差的统计特性。任何一个观测量，客观上总存在着一个能代表其真正大小的数值，这个数值称为该观测量的真值。观测值与真值之差称为真误差，用Δ表示。设三角形内角和的观测值为li，真值为X，则三角形内角和的真误差为：

然后把358个真误差进行统计，得到如表1.1所示的结果。

表1.1　误差统计表

续表

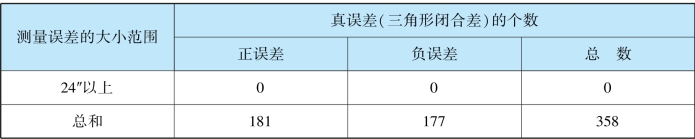
统计时按照3"为一区间，并按绝对值大小进行排列，按误差的正负号分别统计。从表中可以看出该组误差表现出如下规律：误差的绝对值有一定的限值；绝对值较小的误差比绝对值较大的误差多；绝对值相等的正负误差的个数接近。通过更多的实验统计发现，其他测量结果也表现出同样的规律，从而表明偶然误差具有如下统计特性：(www.xing528.com)

①有界性：在一定的观测条件下，误差的绝对值有一定的限值，或者说，超出一定限值的误差，其出现的概率为零。

②误差概率正态分布：绝对值较小的误差比绝对值较大的误差出现的概率大。如图1.14所示，k/n为各区间的频率，dΔ为区间的间隔值；当n趋近于无穷大时，把区间dΔ无限缩小，图1.14中各小长方形的顶边折线就会变成一条光滑曲线，这条曲线称为误差分布曲线，又称正态分布曲线。

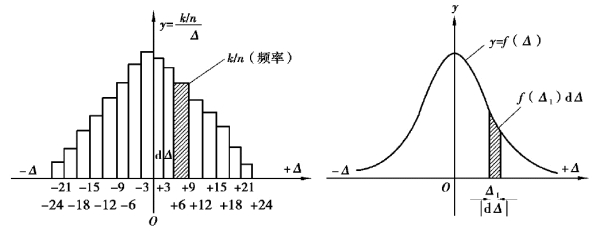
图1.14　误差直方图与误差分布曲线

③对称性：绝对值相等的正负误差出现的概率相同。

④补偿性：当观测次数无限增加时，偶然误差算术平均值的极限为零，即

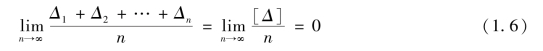
测量工作中为了提高测量成果的精度，通常需要进行多余观测（即超过确定未知量的必要观测数的观测）。这样做可以利用偶然误差的有界性检查测量过程中存在的粗差，还可以利用补偿性提高观测成果的精度。