损伤识别：7.6.1显式时间积分方法

利用中心差分法对运动方程进行显式时间积分时，应用上一个增量步的动力学条件计算下一个增量步的动力学条件。在增量步开始时，求解动力学平衡方程：

其中，M为节点质量矩阵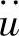；为节点加速度；P为外力；I为单元内力。

在当前增量步开始时（t时刻），计算加速度为：

由于显式算法总是采用一个对角的或者集中的质量矩阵，所示求解加速度并不复杂，不必同时求解联立方程。任何节点的加速度完全取决于节点质量和作用在节点上的合力，使得节点计算成本非常低。

对加速度在时间上进行积分采用中心差分，在计算速度的变化时假定加速度为常数。应用这个速度的变化值加上前一个增量步中点的速度来确定当前增量步中点的速度：

速度对时间的积分加上在增量步开始时的位移以确定增量步结束时的位移：(www.xing528.com)

这样，在增量步开始时提供了满足动力学平衡条件的加速度。得到了加速度，在时间上“显式地”前推速度和位移。所谓“显式”是指在增量步结束时的状态仅依赖于该增量步开始时的位移、速度和加速度。这种方法精确地积分常值的加速度。为了使该方法产生精确的结果，时间增量必须相当小，这样在增量步中加速度几乎为常数。由于时间增量步必须很小，所以一个典型的分析需要成千上万个增量步。但是，因为不必同时求解联立方程组，所以每个增量步的计算成本很低。大部分的计算成本消耗在单元的计算上，以此确定作用在节点上的单元内力。单元的计算包括确定单元应变和应用材料本构关系确定单元应力，从而进一步计算内力，其具体的步骤为：

1）根据应变速率，计算单元应变增量dε。

2）根据本构关系计算应力σ：

σ_（t+Δt）=f（σ_（t），dε） （7-39）

3）集成节点内力I_（t+Δt）。