建筑结构损伤识别：5.2.3改进的子结构模型修正法

子结构修正法要求振型关于质量归一化，而在实际中，大型结构在环境激励下的模态分析很难得到关于质量归一化振型。本文将质量正交方程和刚度正交方程对应元素乘以一个对角为0其他为1的矩阵，建立合理的目标函数进行优化求解，从而改进了子结构模型修正法，使其摆脱对振型归一化要求的限制。

其基本思想为：对有限元模型沿测量自由度方向进行缩聚，形成缩聚的质量矩阵、单元质量矩阵及缩聚的刚度矩阵、单元刚度矩阵。根据实测模态关于缩聚模型正交，并满足缩聚模型的特征方程，建立目标函数，优化得到子结构的修正因子。

根据各单元之间的刚度矩阵的相关矩阵C^K_i，j，划分为M_s个刚度子结构，第i个刚度子结构的刚度矩阵为K_A，j（j=1，2，…，M_s），包括j_Ms个单元，则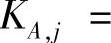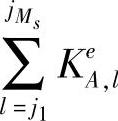，K_A^e_，l为第j个单元的扩展刚度矩阵。根据各单元之间的质量矩阵的相关矩阵C^M_i，j，划分为N_s个质量子结构，第i个质量子结构的质量矩阵为M_A，i（i=1，2，…，N_s），包括i_Ns个单元，则，M_A^e_，l为第l个单元的扩展质量矩阵。

根据缩聚的质量和刚度建立正交方程和特征方程，并忽略正交方程的对角线元素：

当质量矩阵已知，可以把式（5-17）转化为：

当刚度矩阵已知，可以把式（5-16）转化为：

式中 Ⓧ——对应元素相乘；

ξ——对角元素为0，其他元素为1的方阵；

α_i——第i个质量子结构的修正因子；

β_j——第j个刚度子结构的修正因子；

K_A^D_，i——K_A，i关于主自由度的缩阶刚度矩阵；

M_A^D_，i——M_A，i关于主自由度的缩阶质量矩阵；

A_t——实测结构的特征值；

Φ_t——实测结构的特征向量。

式（5-16）表示缩阶质量关于实测振型正交，对应元素乘以ξ表示忽略质量关于振型归一化的条件；式（5-17）表示缩阶质量和缩阶刚度矩阵满足特征方程，并考虑对质量和刚度同时修正；式（5-18）表示缩阶刚度矩阵关于实测振型正交，并只考虑缩阶刚度矩阵关于实测阵型正交的条件。

接下来建立目标函数，由于理论有限元模型存在误差，而且模型缩聚也是近似的过程，因此式（5-16）、式（5-17）、式（5-18）存在误差，设：

定义目标函数：

η=‖Δ₁‖²_F+‖Δ₂‖²_F+‖Δ₃‖²_F（5-24）

其中，‖•‖为Frobenius范数，。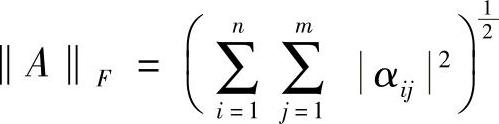

当修正的参数比较多时，也可建立如下的优化函数：

当 Δ₁=0时，η₁=‖Δ₂‖²_F+‖Δ₃‖²_F→min （5-25）

当 Δ₁=0， Δ₃=0时，η₂=‖Δ₂‖²_F→min （5-26）

子结构的质量矩阵和刚度矩阵为对称矩阵，因此质量和刚度矩阵的对称性自然满足。

将式（5-16）、式（5-17）、式（5-18）简化如下：

上面三个公式中：

A_i、B、F_i、G的维数为n_t×n_t，C_j、D_i、E的维数为n_m×n_t。

将式（5-27）、式（5-28）、式（5-29）表示成目标函数，得：

R（∑α_iA_i）=R（B） （5-37）

根据函数的性质，目标A_i、B、C_j、D_i、E、F_j、G进行按列重新排列，则、、、、、、。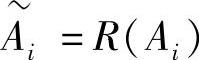

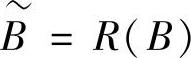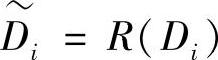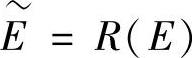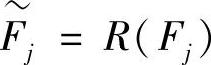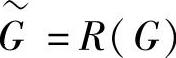将向量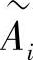、、、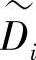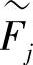形成矩阵：(www.xing528.com)

根据重新排列得到的向量和矩阵，可以改写式（5-27）、式（5-28）、式（5-29），得：

设：

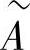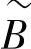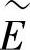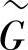α为含N_s个元素的列向量，β为含M_s个元素的列向量，为n²_t行N_s列的矩阵，为含n²_t个元素的列向量，为n_tn_m行M_s列的矩阵，为n_tn_m行N_s列的矩阵，为含n_tn_m个元素的列向量，为n²_t行M_s列的矩阵，为含n²_t个元素的列向量。

将式（5-44）、式（5-45）、式（5-46）三个公式合并成一个方程式，得：

设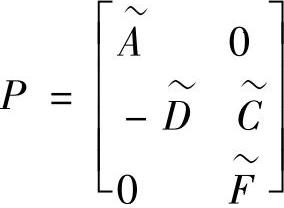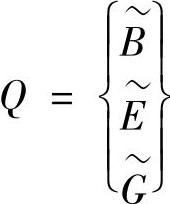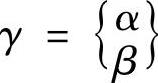，，，则上式简化为：

Pγ-Q=ε （5-51）

P为（2n²_t+n_tn_m）行（N_s+M_s）列的矩阵，Q为含（2n²_t+n_tn_m）个元素的列向量，γ为含（N_s+M_s）个元素的列向量。

因为ε为列向量，所以目标函数可以改写为：

η={ε}^T{ε}={Pγ-Q}^T{Pγ-Q}

=γ^TP^TPγ-γ^TP^TQ-Q^TPγ+Q^TQ （5-52）

当_η取极值时，可求γ的值，由，得：

P^TPγ-P^TQ=0 （5-53）

对于式（5-53）的求解有两种情况：

1）若P的秩等于（N_s+M_s），那么式（5-53）的解是最小二乘解，其解为：

γ=[P^TP]^-1P^TQ （5-54）

2）若P的秩小于（N_s+M_s），式（5-53）的解有无穷个，需要增加约束求解，这里施加解的范数最小这一条件。

根据奇异值分解，可以将P分解为：

P=USV^T （5-55）

式（5-55）中，S是P的奇异值矩阵，为r×r的对角阵，S的对角值是P的奇异值；U为（2n²_t+n_tn_m）×r的矩阵，V为（N_s+M_s）×r的方阵，U^TU=I，V^TV=I。

式（5-53）可以写为：

V^Tγ=VS^-1U^TQ （5-56）

设：P₁=V^T，f₁=VS^-1U^TQ，公式（5-56）转化成：

P₁γ-f₁=0 （5-57）

采用拉格朗日乘子法，求解上述条件极值问题，设拉格朗日函数为：

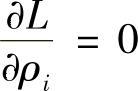然后由L的驻值条件和，得：

γ+P₁^Tρ=0 （5-59）

P₁γ-f₁=0 （5-60）

将式（5-59）代入式（5-60）中，得：

γ=P^T₁（P₁P^T₁）^-1f₁ （5-61）