提高计算效率和精度的方法：划分子结构

合理地划分子结构有助于提高计算效率及计算精度。模型修正时，单元的摄动会引起模型模态的摄动，当实测模态不完整时，测点处对应的模态摄动之间可能存在相关性。以此作为划分子结构的原则，即把对实测模态影响相关性高的单元划分为子结构。

如果直接分析模态摄动的相关性，需要计算模型的模态，计算量较大。假若通过分析缩聚单元之间的相关性，来判断对测量模态影响的相关性，则不必计算特征值和特征向量，将大大减少计算量，提高计算效率。

据此，首先对有限元模型中各个单元的扩展矩阵在测量自由度上进行缩聚，然后求各个单元的缩阶矩阵之间的相关性，把相关性高的单元划分为一子结构，具体过程如下：

假设一结构共n个自由度，m个单元，结构的质量矩阵为M_A，刚度矩阵为K_A。不失一般性，设其中{1，2，…，n_m}为主自由度方向，实测模态为n_t阶。根据模型缩聚方法，可求得缩阶矩阵T。

单元的扩展质量矩阵为M_A，j（j=1，2，…，m），单元的扩展刚度矩阵为K_A，j（j=1，2，…，m），则：

定义矩阵转换函数R。若B=R（A），A为m行n列的矩阵，则B为m×n的列向量，则：(www.xing528.com)

B_k=A_i，j （k=j×m+i-m；i=1，2，…，m；j=1，2，…，n） （5-5）

矩阵转换函数R有如下的性质：

把各个单元扩展刚度矩阵和扩展质量矩阵的缩阶矩阵按列重新排列，成为向量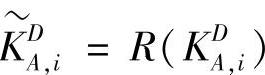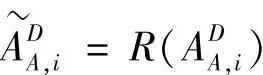，，借用求振型相关性的方法，求重排列向量的MAC值，就得到了各个单元的相关系数C^K_i，j和C^M_i，j。

式（5-9）中，x、y为维数相同的列向量。根据单元的相关系数C^K_i，j和C^M_i，j矩阵，划分刚度子结构和质量子结构。