解析法识别建筑结构损伤：仅需35分钟，并保持准确度

算例一：用非线性解析法计算第2章的算例。

选用前45阶无损和有损频率及前35阶有损和无损振型作为输入值。计算结果见表3-1。

表3-1 无迭代的非线性、线性解析法计算结果及其真实值

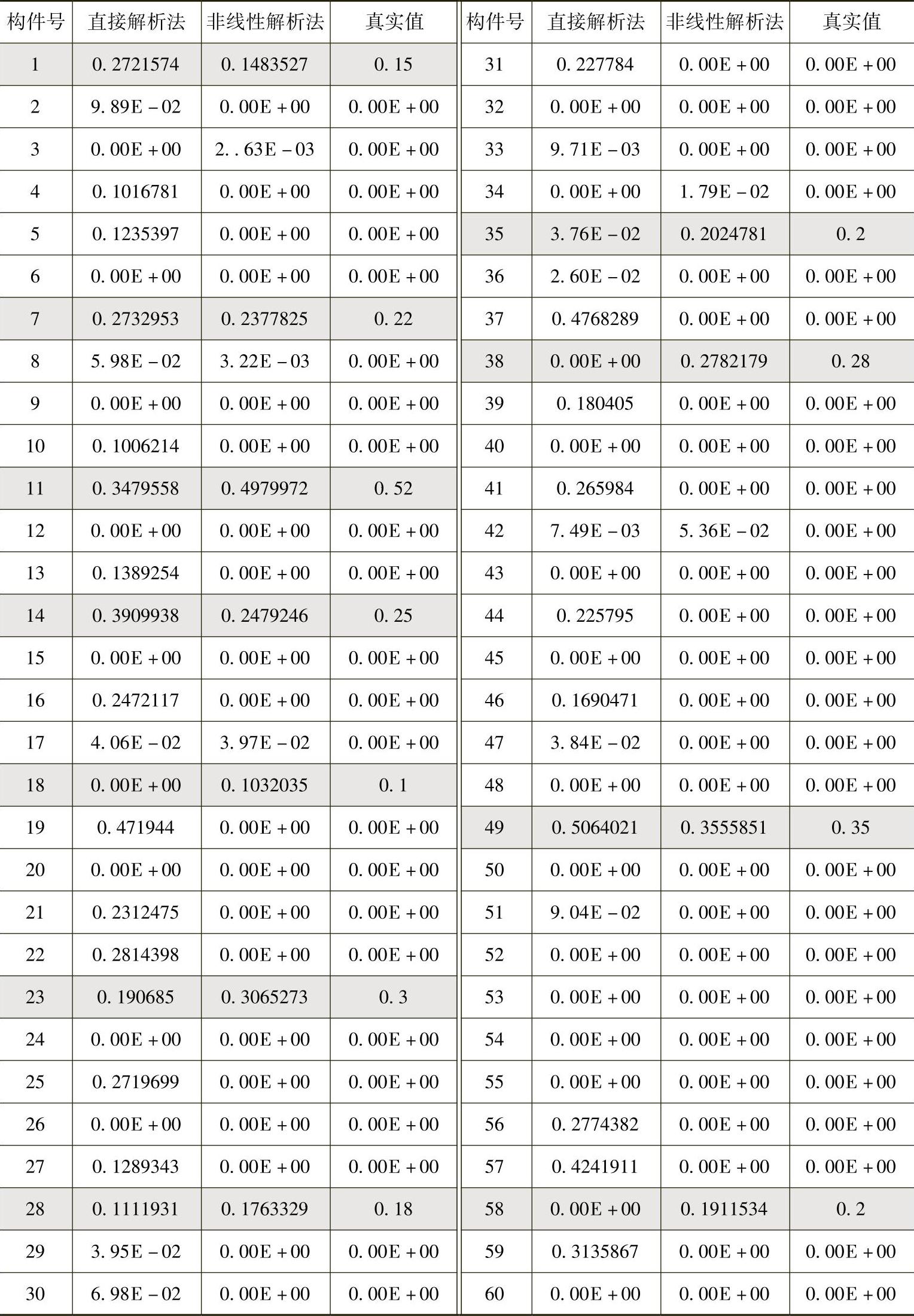
从计算结果可以看出，非线性解析法的解与真实值基本吻合，仅有少量值略大于或略小于真实值，如构件11、17、34、42，但其误差也均在5%以内，从实际工程角度来看，这比较满意地达到了损伤检测要求。通过解值能够确定损伤的程度，而从相应的构件号可以判定损伤的位置。这个算例充分验证了非线性解析法的可行性和精确性，它可以同时识别出结构损伤的数量、位置和程度。

另一方面，线性解析法的解与真实值差别就很大，如构件4、5、10、13、16等本来就没有损伤，但其计算值却较大，19号无损构件的计算值竟达到0.47，而如损伤构件1、11等计算值也与真实损伤值相去甚远，这些在实际工程中是无法容忍的。造成此结果的根本原因在于在构建超定线性方程组时，只取泰勒级数的一次近似项，结果精度有限。因此必须用自迭代修正技术对其进行改善，以提高精度。

表2-4中线性解析法第六次自迭代修正结果的损伤值，与无迭代修正的非线性解析法相比，其识别精度相当，但就计算所需时间而言，线性解析法比非线性解析法用时多五倍。本算例仅有60个元素，非线性解析法约需35分钟，而要达到同样的精度，线性解析法需175分钟以上。实际工程中，复杂结构包含上千个元素，线性解析法需自迭代几十次甚至上百次才能达到需要的精度，与非线性解析法相比，既过多占用计算机资源又浪费时间。

算例二：一个四层单跨的钢筋混凝土框架结构。

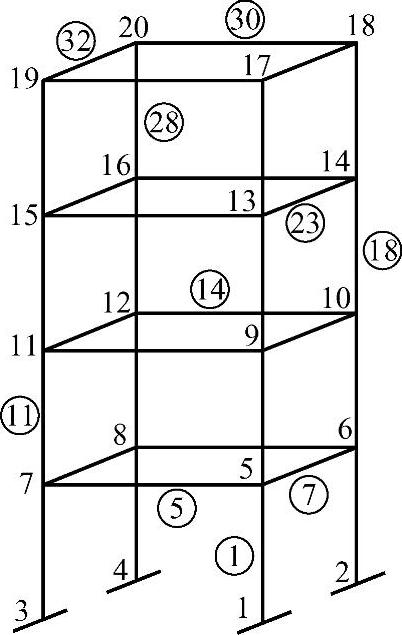
跨度为4m，层高为4m，泊松比为0.3，弹性模量为2.55GPa，密度为2.5t/m³，梁柱截面为0.35m×0.35m。共有20个节点，32个构件。假设该结构有10个构件产生损伤，损伤位置与程度分别见图3-3和表3-2。用非线性解析法反演它的损伤值。

(www.xing528.com)

图3-3 四层框架结构的计算简图

表3-2 单元损伤值

利用程序ADINA计算出前50阶有损和无损频率及振型，选取前20阶无损和有损频率及前15阶有损和无损振型作为输入值，计算结果见表3-3。

表3-3 非线性解析法计算结果及其真实值

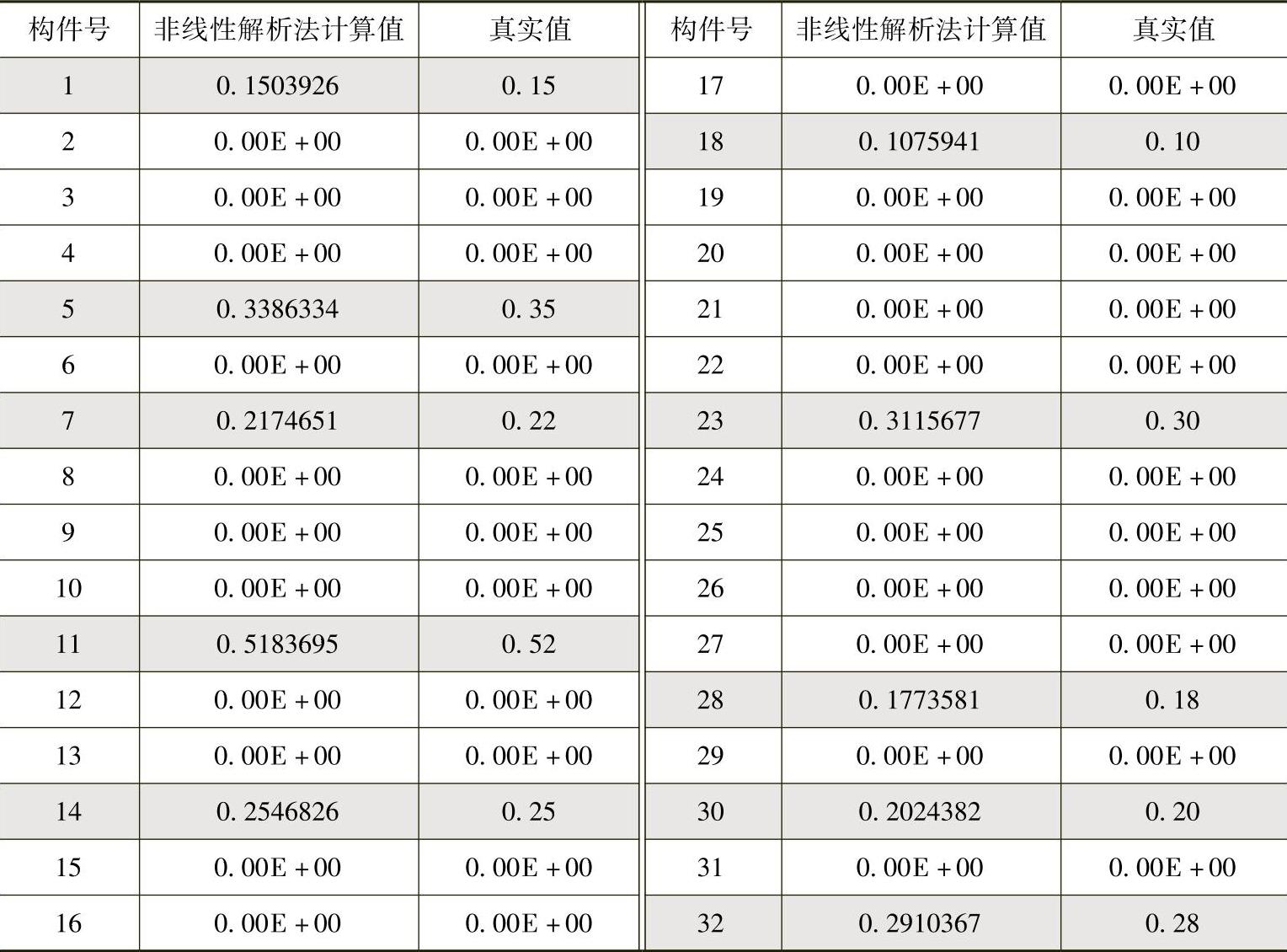
从表3-3可以看出，非线性解析法在结构较少构件的情况下，无需自迭代修正技术也能获得较精确的结果。对于较复杂的结构，才需要自迭代修正其计算结果。固有频率是一个结构的全局特性，这种参数不可能诊断出除了损伤存在之外的信息，即固有频率通常不可能提供有关结构动力特性变化的空间信息。另外，单就固有频率的变化不能识别出对称结构中对称位置上的损伤，也不能识别出多损伤工况下结构损伤的位置。本算例是一个对称结构，从结果来看，解析法结合了频率对损伤较为敏感的特性和振型能够反映结构空间信息的特征，不仅成功地识别出结构损伤的位置、大小和数量，而且，对于对称结构仍然有效。

前面已经提到：对于大型复杂的结构而言，在实际的损伤诊断中无法测出高阶模态。上面两个算例虽然都较为简单，但依然使用了高阶频率和振型。