广义逆法求解非线性方程组

设非线性方程组：

f_i（x₁，x₂，…，x_n）=0 （i=1，2，…，mm≥n） （3-19）

其中f_i为连续函数，且f_i中至少有一个为非线性函数。

取解的初始近似（x₁^（0），x₂^（0），…，x_n^（0）），将f_i函数在（x₁^（0），x₂^（0），…，x_n^（0））点作一阶泰勒展开，忽略余项，取x₁，x₂，…x_n的线性函数为近似函数，得：

式（3-20）中x^（0）=（x₁^（0），x₂^（0），…，x_n^（0））T。

利用线性方程组的广义逆法可解出x₁，x₂，…x_n，记作（x₁^（1），x₂^（1），…，x_n^（1）），称为式（3-19）的一次近似解。将（x₁^（1），x₂^（1），…，x_n^（1））放在上述（x₁^（0），x₂^（0），…，x_n^（0））的位置继续进行可得二次近似解（x₁^（2），x₂^（2），…，x_n^（2））。一般地，设（x₁^（k），x₂^（k），…，x_n^（k））为k次近似解，则式（3-20）变成：

其雅可比矩阵为：

同样可解出x₁，x₂，…x_n，记作（x₁^（k+1），x₂^（k+1），…，x_n^（k+1）），称为式（3-19）的k+1次近似解。从而，得到求解式（3-19）的迭代式：

x^（k+1）=x^（k）-（A^（k））+F^（k）（3_-23）

式（3-23）中A^（k）为k次迭代值x^（k）的雅可比矩阵；F^（k）为k次迭代值的左端函数值，即：

F^（k）=（f₁^（k），f₂^（k），…，f_m^（k））T

f_i^（k）=f_i（x₁^（k），x₂^（k），…，x_n^（k）） （i=1，2，…，m） （3-24）

上面对非线性方程组的求解实际上转化成了线性方程组的求解，下面分析齐次方程组的解法。

考虑非齐次线性方程组AX=b（3-25）(www.xing528.com)

其中A∈C^m×n，b∈C^m给定，而X∈Cⁿ为待定向量，m＞n。

当rank（A︙b）≠rank（A），即方程组无解或称方程组不相容时，则不存在通常意义下的解，但在本问题中，可以求出最小二乘解：

‖AX-b‖₂=min （3-26）

其中，‖•‖₂是Euclid范数。

一般来说，矛盾方程组的最小二乘解不是唯一的，但在最小二乘解的集合中，具有唯一的最佳逼近解：

X=A⁺b （3-27）

这里，广义逆矩阵A⁺是利用Householder变换及变形QR算法对矩阵A进行奇异值分解得到的。对于A，存在一个m×m阶的列正交矩阵U和n×n阶的列正交矩阵V，使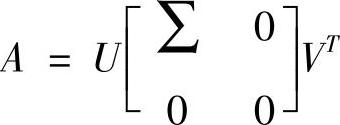：成立。

其中∑=diag（σ₁，σ₂，…，σ_r） （r≤min{m，n}）且σ₁≥σ₂≥…≥σ_r＞0。

设U=（U₁，U₂），其中U₁为U中前r列列正交向量组构成的m×r阶矩阵；V=（V₁，V₂），其中V₁为V中前r列列正交向量组构成的n×r阶矩阵。则A的广义逆矩阵A⁺为：

A⁺=V₁∑^-1U₁^T （3-28）

将式（3-28）代入式（3-27）中，得最佳逼近解：

X=V₁∑^-1U^T₁b （3-29）

对于特大型复杂的结构，非线性解析法必然构造特大型超定非线性方程组，这在单机处理系统中无法求解，必须借助于多处理系统的并行算法予以实现。其基本思想是：将方程组适当地划分为互不重复的N块，相应地得到N个最优化子问题，最后，求解这N个最优化问题，并将所得的解予以组合，即得到原问题的一个近似解。本书对此不作详细探讨，仅提出一种思路。