【摘要】:本算例为一个五层两跨的钢筋混凝土框架结构。单跨跨度为8m,层高为4m,泊松比为0.3,弹性模量为2.55GPa,密度为2.5t/m3,梁柱截面为0.4m×0.4m。共有34个节点,60个构件。假设该结构在一地震载荷作用下有11个构件产生损伤,损伤位置与程度分别见表2-1和图2-1。现来验证线性解析法的可行性。从表2-4的6次迭代结果来看,11个损伤构件位置均被识别出来,其损伤值误差均在设定的范围之内。
本算例为一个五层两跨的钢筋混凝土框架结构。单跨跨度为8m,层高为4m,泊松比为0.3,弹性模量为2.55GPa,密度为2.5t/m3,梁柱截面为0.4m×0.4m。共有34个节点,60个构件。假设该结构在一地震载荷作用下有11个构件产生损伤,损伤位置与程度分别见表2-1和图2-1。现来验证线性解析法的可行性。
表2-1 单元损伤值

运用ADINA软件计算出此结构损伤前后的前50阶频率和振型,选用前45阶无损和有损频率及前35阶无损和有损振型作为开始输入值,分别见表2-2和表2-3(由于篇幅有限,仅列出前2阶的振型)。
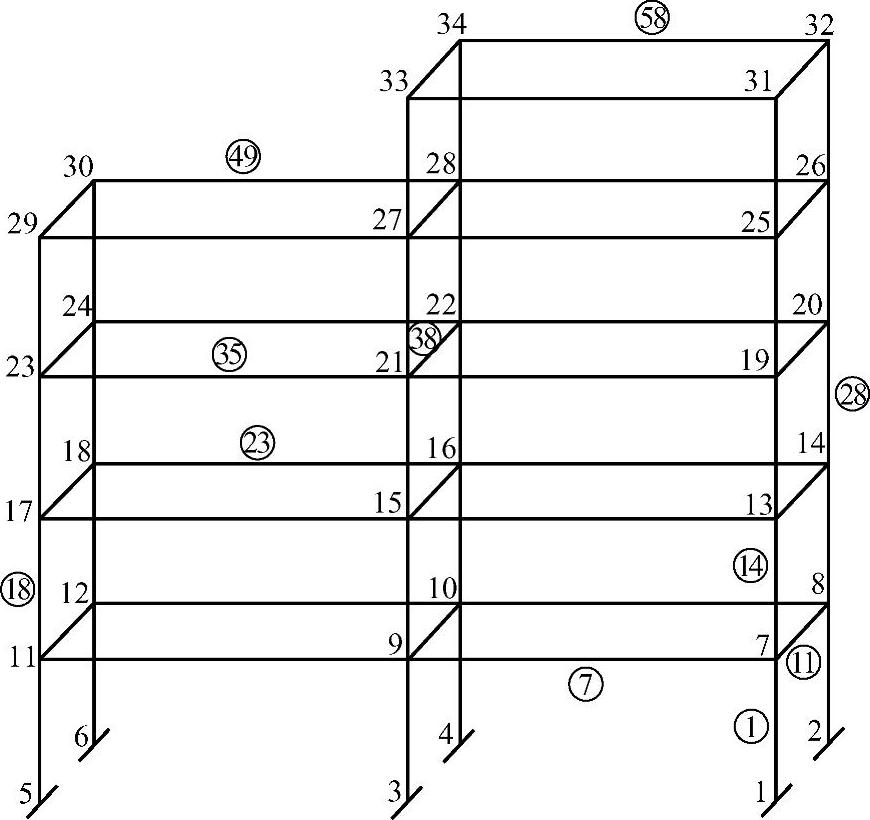
图2-1 计算简图
表2-2 前45阶无损和有损频率

(续)

表2-3 前2阶无损和有损振型
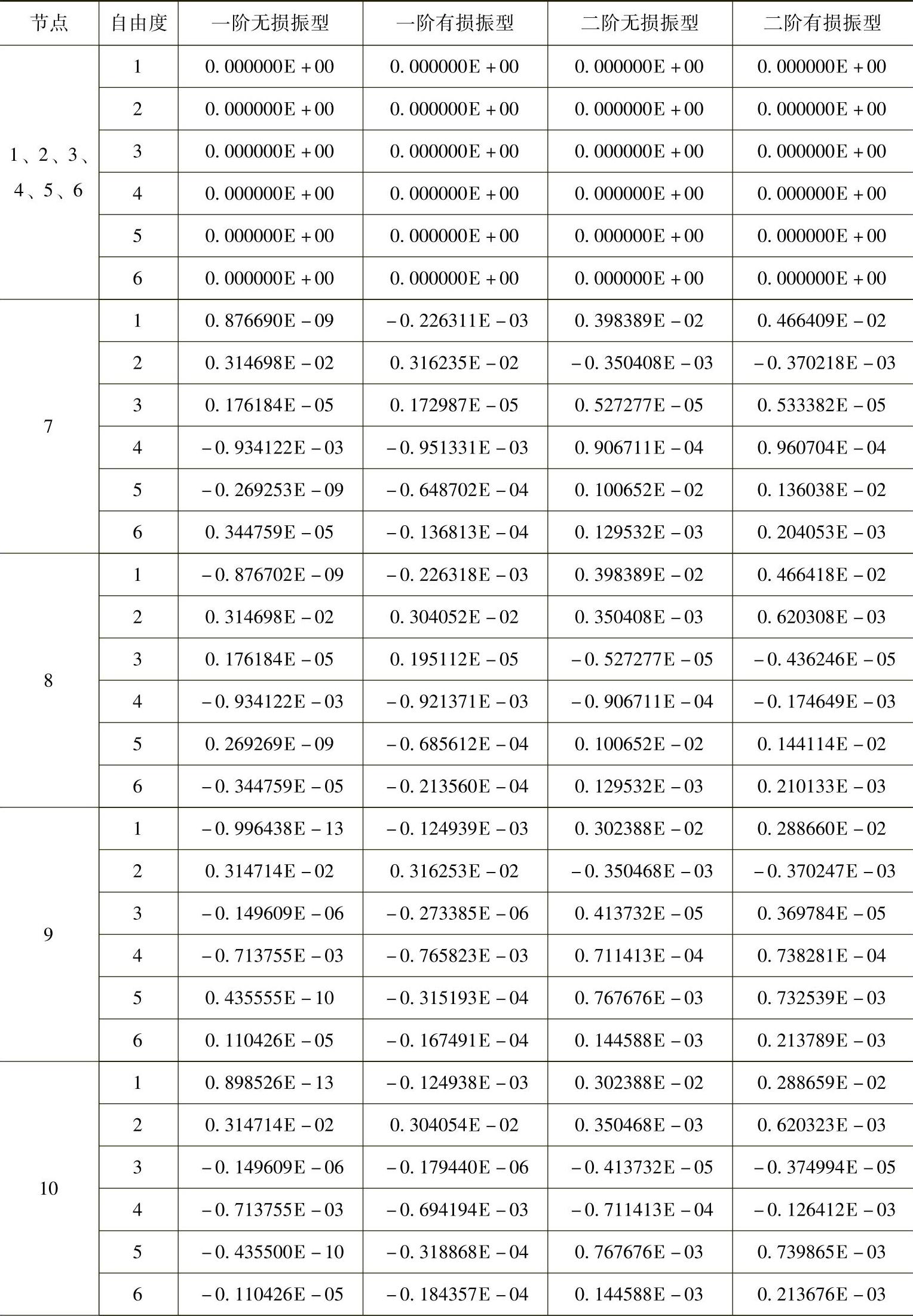
(续)

(续)

(续)(https://www.xing528.com)

(续)

(续)

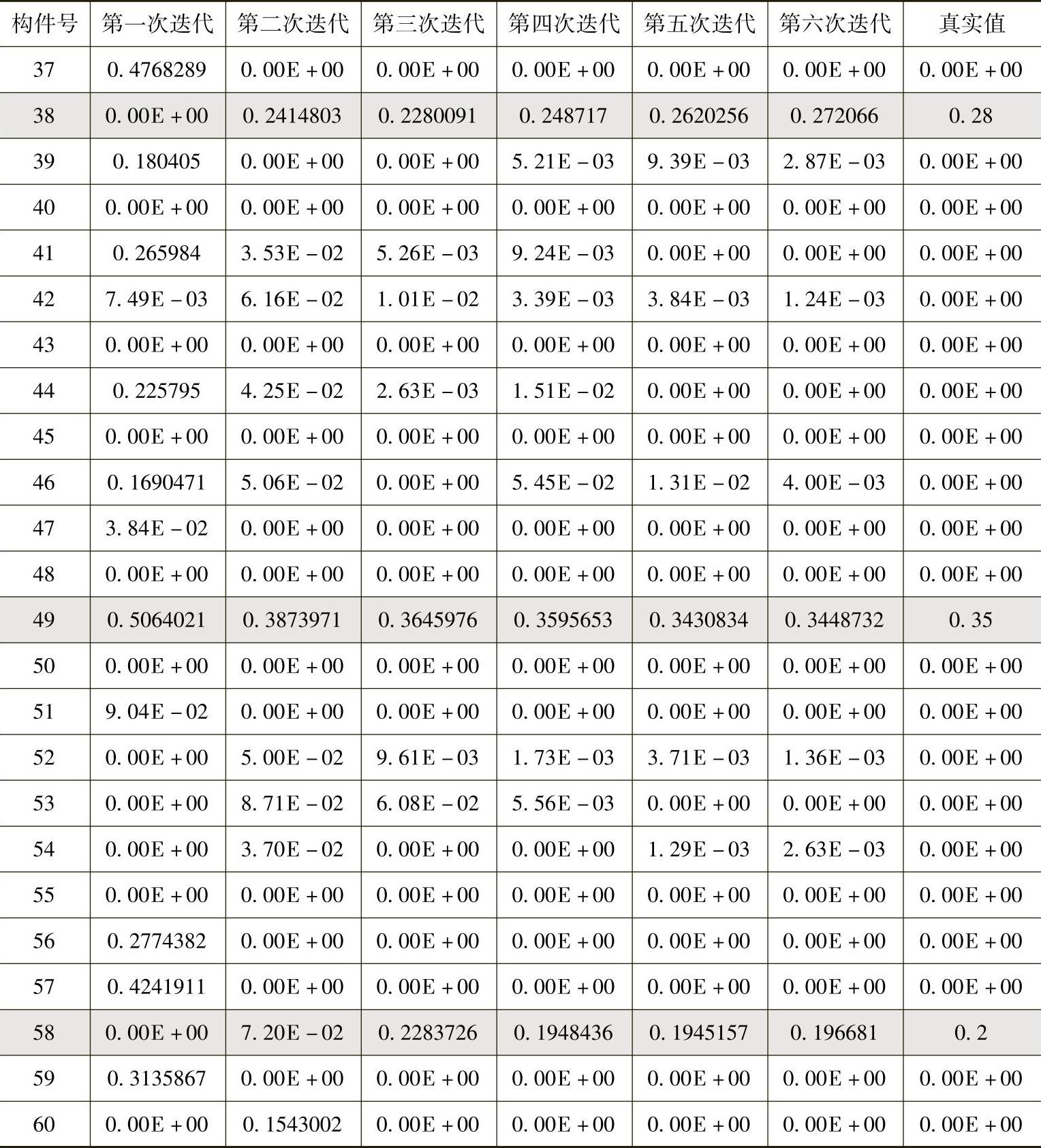
经6次自迭代修正计算,其识别结果见图2-2和表2-4。从表2-4的6次迭代结果来看,11个损伤构件位置均被识别出来,其损伤值误差均在设定的范围之内。而无损构件的损伤值绝大多数为零,只有极少数构件接近零,但与损伤构件的值相差甚远,在实际工程中,可视为零值。比较图2-2与图2-3,单元损伤值识别做到动态地逼近真值,可见自迭代修正的解是收敛的。

图2-2 六次迭代过程
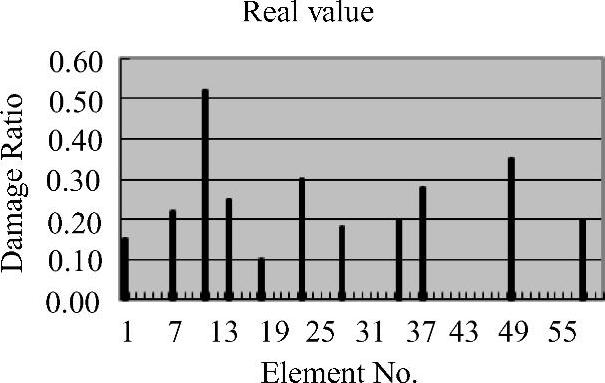
图2-3 真实损伤值
表2-4 损伤迭代结果及其真实值

(续)

(续)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




