建筑结构损伤识别的基本理论与表达式

根据损伤力学理论，框架结构中第i根构件中拉压、弯曲、剪切刚度计入损伤系数时的表达式为：

式（2-1）中，D_i为第i构件（或单元）的损伤参数；下标“0”表示未受损伤时构件的原始刚度。D_i在0或1取值，D_i=0时，表示第i构件完好无损；D_i=1时，表示第i构件完全破坏；在0＜D_i＜1区间内，表示第i构件不同程度的损伤状态。

对于线弹性有限元模型，动态控制方程表达式为（认为损伤不会引起质量的改变）：

式中，U、、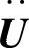分别为N维（N为结构自由度总数）位移、速度和加速度向量；M为未损结构质量矩阵；C为阻尼矩阵；K_d为损伤结构刚度矩阵。

进行模态分析时，其特征值问题表达式为：

K_dΦ_r=ω_r²MΦ_r （2-3）

式（2-3）中，ω_r为已损结构的第r阶固有频率，Φ_r为相应的振型，Φ_r可表示为：

Φ_r=[φ_1r，φ_2r，…，φ_Nr]^T （2-4）

式（2-4）中，N为结构的自由度数，振型正则化后，具有下式特征：

式（2-5）中，(www.xing528.com)

把频率ω_r和Φ_r作为损伤参数D_i（i=1，2，…，L）的函数，其中L代表单元总数。将ω_r和Φ_r展开为D_i的泰勒级数，得：

上两式中，ω_r⁰、Φ_r⁰分别为未损结构的第r阶固有频率和振型。保留上两式右边的一次项，则已损结构与未损结构的频率差、振型差分别为：

线性解析法用已知的Δω_r、ΔΦ_r（r=1，2，…，nn≤N）来求解损伤参数D_i，具体的方程为：

Δf=SD （2-10a）

式（2-10a）中，Δf为频率、振型差列阵，表达式为：

D表示待求的损伤参数列阵，表达式为：D={D₁，D₂，…，D_L}^T_1×L；S为频率及振型对损伤参数一阶偏导矩阵，表达式为：

将式（2-10a）求广义逆，即可求出所需的损伤参数：

D=S^-1Δf （2-10b）

下面将推导S阵中各元素算式。