建筑结构损伤识别与损伤本构方程研究

由建筑的损伤特点，认为结构存在的损伤为各向同性损伤，采用几何损伤理论建立损伤本构方程。

几何损伤理论认为损伤造成的实际承载面积的减少是材料劣化的主要原因。一维情况下，假定有一受单轴拉伸的试件，受拉力P，存在损伤D，截面积为A，构件可分为不考虑损伤的无损构件、考虑损伤的损伤构件与虚拟无损构件，虚拟无损构件的有效承载面积为A∗。

无损构件的表观应力σ为：

损伤D：

虚拟无损构件中，有效应力σ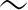与表观应力σ的关系为：

J.Lemaitre在1971年提出了应变等价性假说，认为应力作用在受损材料上引起的应变与有效应力作用在无损材料上引起的应变等价。由这一原理，受损结构的本构关系可通过无损结构本构关系中的表观应力改为受损材料的有效应力而获得。计算中将每个构件当成弯曲梁，按单元处理，其应力矩阵与广义位移矩阵分别为：

{P_i}=[N_xiN_yiN_ziM_xiM_yiM_zi]^T （1-4）(https://www.xing528.com)

{δ_i}=[u_iv_iw_iθ_xiθ_yiθ_zi]^T （1-5）

单元横截面积为A，xz面内截面惯性矩为I_z，xy面内截面惯性矩为I_y，单元扭转惯性矩为J，长度为L，弹性模量为E，泊松比为μ，剪切模量G=E/2（1+μ）。则无损构件力与位移的本构方程为：

{P_i}=[K^e]{δ_i} （1-6）

设该单元存在损伤D_i，则损伤构件的本构方程为：

式（1-7）中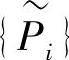，为有效杆端力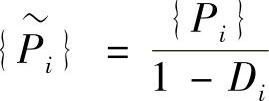，，由式（1-6）和式（1-7）可以得到损伤单元的本构方程：

式（1-8）中，[K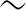e]=（1-D_i）[K^e]，[K^e]见式（1-9）。