动力电池热流场仿真分析的基本控制方程

将仿真分析应用于散热系统的产品开发过程中，可以缩短其开发周期、降低开发成本、提升开发过程中的理论水平，并可以检验产品开发过程是否偏离正确的方向。从仿真分析的特性来看，散热系统的设计验证主要涉及热流场仿真分析与相变仿真分析，如液冷系统与风冷系统的仿真主要为热流场仿真分析，而相变冷却的仿真主要为相变仿真分析。

2.3.3.1 热流场仿真分析

仿真分析是获取电池系统内部热场和流场的一种十分有效的方法，借助仿真工具对电池系统内部热场和流场进行理论分析，可以在很大程度上缩短开发周期、节省开发成本，并且提高冷却系统的可靠性。仿真分析流程如图2.31所示。

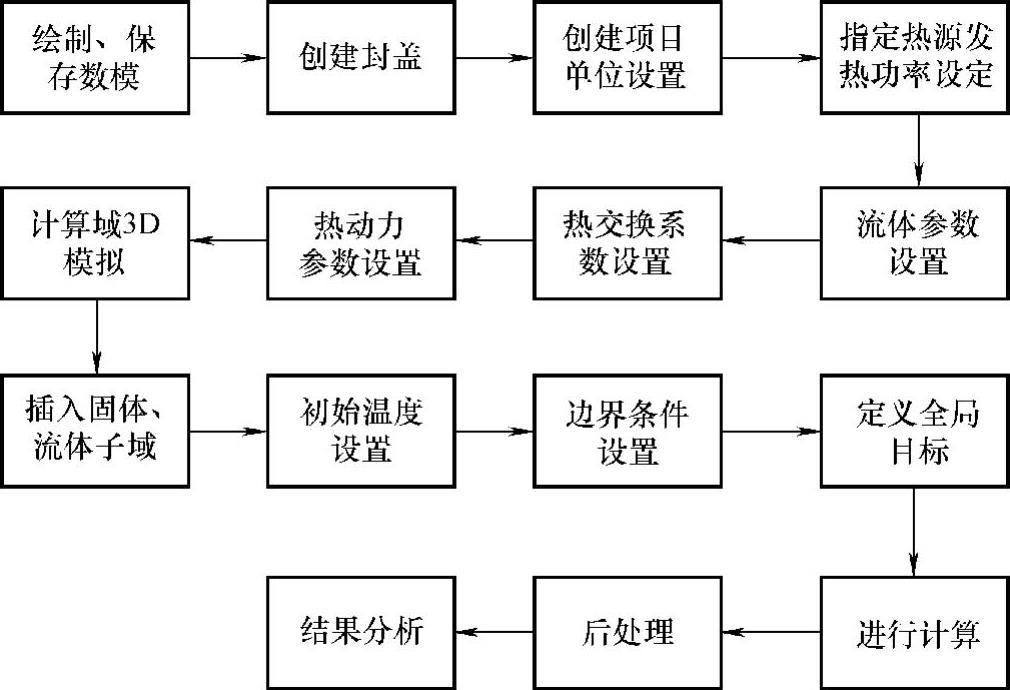
图2.31 热流场仿真流程图

自然界中任何流体流动都需遵守自然界三大基本定律，即质量守恒定律、动量守恒定律和能量守恒定律。这也是电池包热流场仿真分析的理论基础，也称为基本控制方程。

（1）质量守恒方程

质量守恒定律，在流体力学中也称为连续性方程。FLUENT软件采用基于有限元方法对控制方程进行离散，即在流场中任取一流体微元体dxdydz，单位时间内该微元体增加的质量等于同一时间段内流入该微元体流体的质量与流出该微元体流体的质量之差。其完整的数学表达式为：

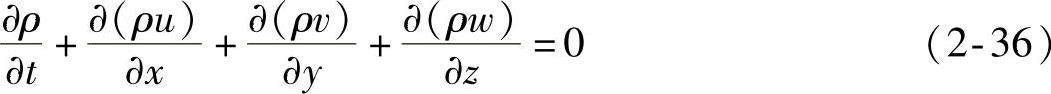
式中，u，v，w分别是流体微元速度矢量u在x，y，z三个方向上的分量；ρ为微元所在地流体密度，单位为kg/m³；t为时间，单位为s。

（2）动量守恒方程

动量守恒定律，实质上是牛顿第二定律在流体力学中的另一种表达方式。仍在流场中任取一流体微元体dxdydz，单位时间内该微元体动量的增量等于同一时间段内流入该微元体的净动量与作用于该微元体上的外力之和。其完整的数学表达式为：

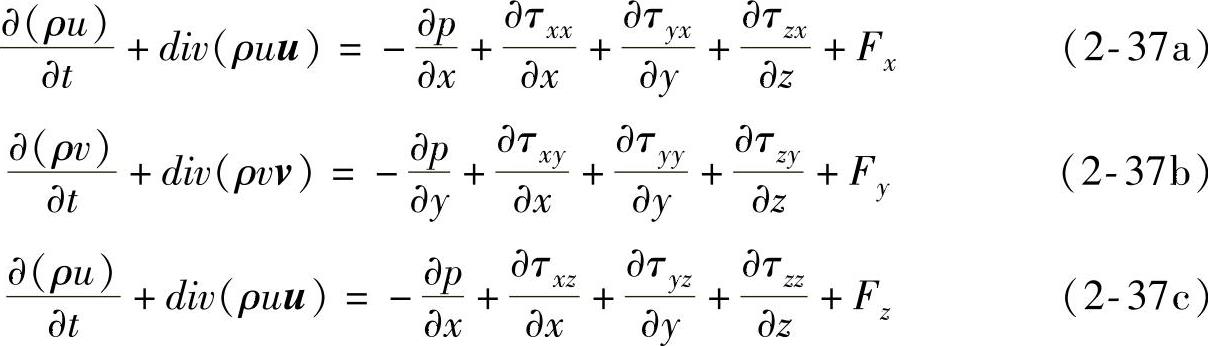(www.xing528.com)

式中，p为微元体受到的压力，单位为Pa；τ_xx、τ_yx、τ_zx等为微元体表面黏性应力τ的分量，单位为Pa；F_x、F_y、F_z为作用在x，y，z三个方向上的体积力，单位为N。对于亚声速低马赫数不可压缩（Ma<0.3）流体，上述方程可转化为经典的N-S方程。

（3）能量守恒方程

能量守恒定律，实质上是热力学第一定律的另一种表达。即流体微元体dxdydz单位时间内能量的增量等于同一时间段内流入该微元体的能量、外界对微元体做的功以及外界传递给微元体的热量之和。其完整的数学表达式为：

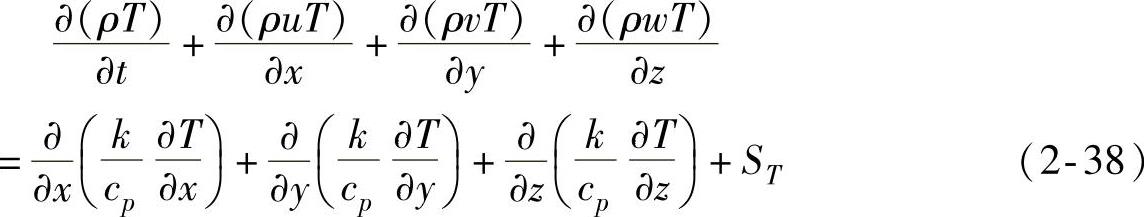
式中，T为热力学温度，单位为K；k为流体导热系数，单位为W/（m·K）；c_p为比定压热容，单位为J/（kg·K）；S_T为黏性耗散项，考察机械能经由黏性摩擦力转化成热能的程度。

在常规工况下，电池系统内部的传热和流体流动过程并不是特别复杂，常用的商业软件（如Fluent和Star CCM+等）都可以十分精确地仿真出电池系统内部的热流场分布和流场分布。虽然如此，对流场和传热理论基础的深入理解，仍然是保证仿真精度的必要条件。

2.3.3.2 相变仿真分析

相变材料是指当材料本身的温度到达临界温度（相变温度）时，材料发生相变的同时从周围吸收热量或者向周围释放热量，并且相变材料自身的温度在相变过程中几乎没有变化，相变时吸收或者释放的这部分热量也称为相变潜热。

散热系统中的相变材料可以利用仿真工具进行辅助设计，Ling等对相变储热材料的热力学过程进行了描述，如式（2-39）～式（2-43）所示。

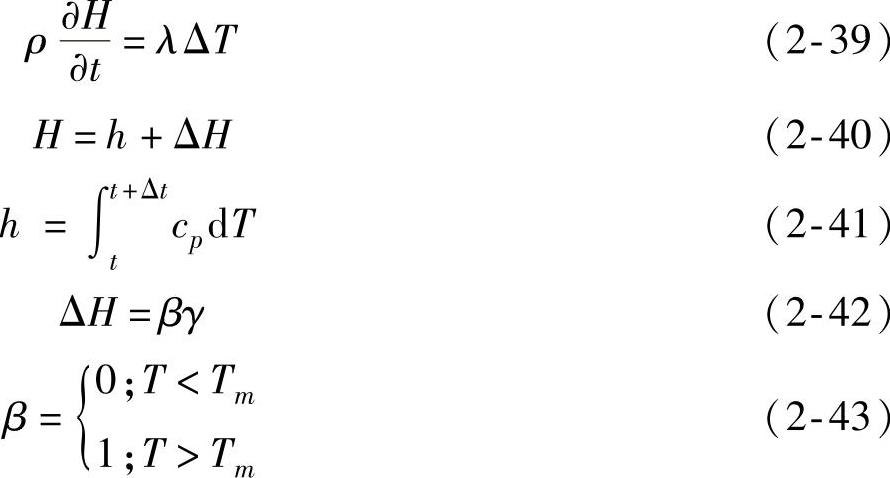
式中，ρ为相变储热材料的密度；λ为相变储热材料的导热系数；T为相变储热材料的温度；h为相变材料的比焓；γ为相变材料的相变潜热；T_m为相变材料的相变温度点。