1.CFAR检测
地波雷达的CFAR检测处理通常在距离向和多普勒向分别进行,完成两个维度的CFAR检测后,再综合距离向、多普勒向检测结果,结合峰值检测的结果,输出最终检测结果。地波雷达CFAR检测处理流程如图6.20所示。
常用的地波雷达CFAR检测方法有均值类恒虚警检测器(CA-CFAR)、排序统计类恒虚警检测器(OS-CFAR)和自适应回归CFAR检测器。其中,CA-CFAR检测方法适合均匀背景噪声的区域,但受地杂波、一阶海杂波以及电离层干扰的影响较大,容易导致噪声估计过高,造成检测性能下降。OS-CFAR检测方法对弱杂波具有一定的抑制能力,在强杂波区检测性能下降。自适应回归CFAR检测方法对电离层干扰、低速区杂波干扰具有一定的抑制效果,但在均匀检测背景区,检测性能不如CA-CFAR和OS-CFAR。通常情况下,为得到更好的检测结果,在实际检测过程中,可以先对RD谱进行分割,识别出不同杂波区,然后基于不同杂波类型选择适合的CFAR检测方法,整体提高检测性能。
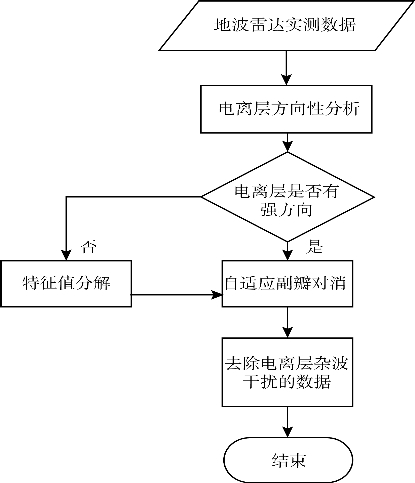
图6.19 基于方向特性分析的电离层杂波抑制方法流程
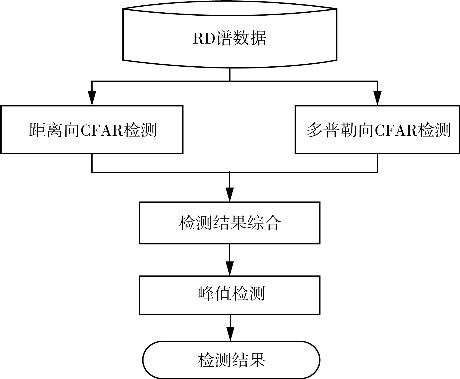
图6.20 地波雷达CFAR检测流程
(1)CA-CFAR方法
CA-CFAR检测器利用参考窗内的雷达回波均值估计噪声水平,其结构如图6.21所示。输入信号xi被送到长度为N(N=2L+1)的寄存器组中,对被检测单元周围N个参考单元求均值,其结果便为噪声估计μ,检测门限U0=Kμ,门限因子K则用于虚警率控制。
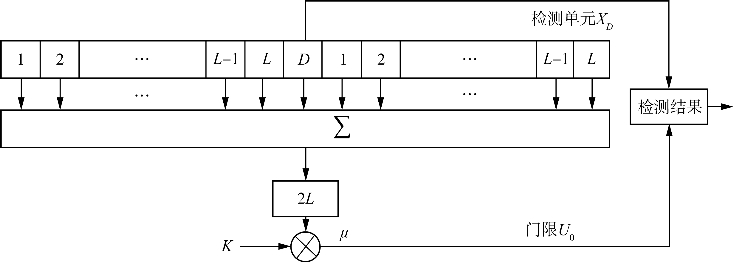
图6.21 CA-CFAR检测器原理
CA-CFAR是最基本的一种CFAR检测算法,在均匀杂波背景下,当参考窗长度趋近于无穷时,可达到理想检测器的性能。但是在杂波边缘和多目标环境下,噪声的估计值将会偏高,导致目标漏检,缺乏鲁棒性。一般来说,滑窗范围越大,CFAR损失越小,但可能无法形成有效的局部估计。
(2)OS-CFAR检测方法
OS-CFAR检测器中,输入信号xi被串行输入到长度为2L+1的寄存器组中,xD是待检测单元,其两侧各有长度为L的参考单元。将参考单元中N(N=2L)个信号的值排序,取出其中第k个最小值xk,xk即为噪声估计值μ。则检测门限为U0=Kμ,其中门限因子K用于控制虚警率的大小。OS-CFAR检测器原理如图6.22所示。
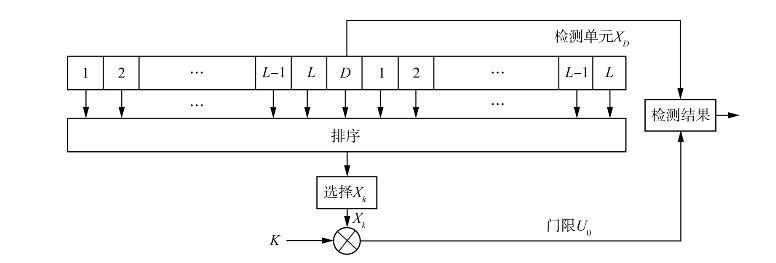
图6.22 OS-CFAR检测器原理
OS-CFAR检测方法由于存在排序过程,可以有效避免异常值对噪声估计的影响,对杂波环境的适应性较强。
(3)自适应回归CFAR检测方法
自适应回归检测器采用曲线回归方法拟合功率谱,获得噪声整体估计。雷达回波信号输入自适应回归检测器形成功率谱,通过曲线回归分析对功率谱进行曲线拟合,拟合出的结果即为噪声估计,将噪声估计值乘以门限因子K获得检测门限,通过K控制虚警率的大小。自适应回归CFAR检测器原理如图6.23所示。
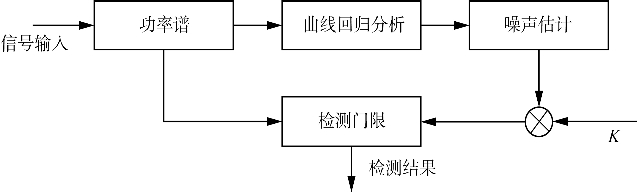
图6.23 自适应回归CFAR检测器原理
自适应回归CFAR检测器对功率谱的整体进行曲线拟合而获得噪声估计,对杂波环境的适应性更强。图6.24给出了雷达RD谱的CFAR检测结果。

图6.24 雷达RD谱的CFAR检测结果
2.目标跟踪
目标跟踪作为地波雷达目标检测跟踪系统中的最后也是最复杂的一环,担负着降低虚警与形成航迹的任务,是目标探测跟踪效果的直接体现。
目标航迹跟踪利用雷达探测得到的多时刻的目标点迹推演出目标的真实航行轨迹,由多目标跟踪算法实现,主要涉及航迹起始、航迹维持与航迹终结三个阶段,其中,最重要的是航迹维持,它由状态预测、数据关联与状态滤波三个主要环节构成,是一个由关联和估计构成的循环过程。跟踪算法的流程如图6.25所示。
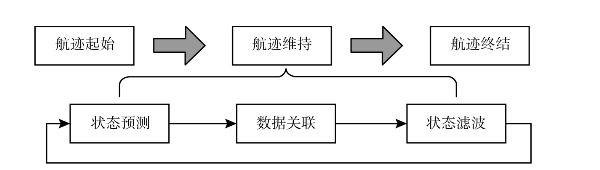
图6.25 高频地波雷达航迹跟踪流程
地波雷达目标跟踪算法以目标运动模型及测量模型的建立为基础,在该模型下,进行航迹起始、维持与终结三个航迹管理过程,下面分别对上述模型及航迹管理过程进行介绍。
(1)目标的运动模型与测量模型
1)状态方程
目标跟踪以目标运动的状态方程和量测方程为核心,跟踪开始前,首先需要确定目标的运动模型与测量模型。目标的运动模型反映了目标下一时刻的运动状态与当前状态的关系,通常在笛卡儿坐标系中定义:
![]()
式中,f k(·)表示k时刻的非线性函数,x k为目标的运动状态矢量,ωk为过程噪声。对于海上大型的舰船目标,一般采用匀速(Constant Velocity,CV)模型进行状态预测,预测模型如下:
![]()
式(6.69)中,x k=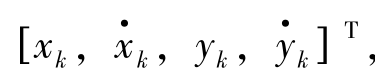 其中,xk、yk分别表示目标沿x、y方向的坐标位置分量,
其中,xk、yk分别表示目标沿x、y方向的坐标位置分量,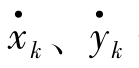 分别表示两个方向上相应的速度分量。
分别表示两个方向上相应的速度分量。

Tk为当前的采样时间,v k考虑到了目标的加速度以及未被建模的运动特性,一般认为其服从均值为零、协方差矩阵Q k=σv
2 I的高斯分布。
除了匀速模型外,对于大型的海上舰船目标,常用的模型还有匀加速(Constant Acceleration,CA)模型、目标存在机动时采用的Singer模型、“当前”统计模型等。由于目标运动的复杂性,仅利用单个模型往往很难准确地描述其运动状态,目标的运动模式可在多种模型间切换,由此提出了交互多模型IMM(Interacting Multiple Model)的方法,它利用多个模型的相互作用得到目标的状态估计;而预测模型体现在状态方程中相邻时刻目标状态的转移矩阵上。
2)量测方程
量测方程反映了目标的测量状态与其真实状态之间的关系。假设雷达位于球坐标系的原点,则目标的测量方程可以表示为:
![]()
地波雷达采用目标的距离、方位角及径向速度来描述目标的状态,因而公式(6.70)可以具体表达为:
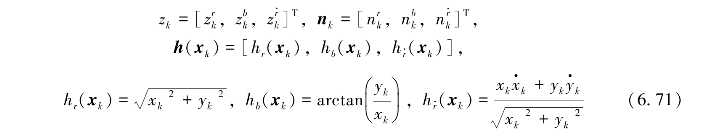
式(6.71)中,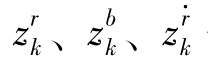 分别表示目标的距离、方位角及径向速度的测量值;一般将量测噪声向量n k建模为均值是零、协方差矩阵
分别表示目标的距离、方位角及径向速度的测量值;一般将量测噪声向量n k建模为均值是零、协方差矩阵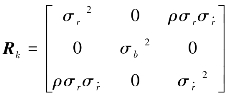 的高斯随机变量。一般地,噪声分量
的高斯随机变量。一般地,噪声分量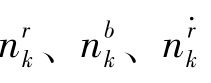 之间通常被认为是统计独立的变量,除了
之间通常被认为是统计独立的变量,除了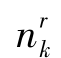 与
与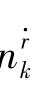 之间具有相关系数为ρ的相关性。但是,对高频地波雷达而言,无法直接获取ρ的信息,因此,假设其值为零。
之间具有相关系数为ρ的相关性。但是,对高频地波雷达而言,无法直接获取ρ的信息,因此,假设其值为零。
(2)航迹管理
航迹管理包括:航迹的形成与终结,关联波门的确定与数据关联,状态预测、更新与滤波等过程。分别介绍如下:(https://www.xing528.com)
航迹形成一般采用M/N逻辑法进行航迹起始,在满足M/N逻辑的条件下,量测序列被确认为一条合法的航迹。在航迹形成的过程中,对地波雷达目标位置量测作如下考虑:
①每一个未关联的量测都作为新的航迹头起始航迹,也即形成一条假定航迹(tentative track)。
②当有新的量测数据到来时,对于每一个航迹头建立关联波门,波门的设置需要考虑以下两点:a.考虑到目标运动参数的最大值/最小值;b.量测噪声的强度,即如果一个航迹头是一个真实的目标点,那么在下一帧数据中,应使得该目标的点迹量测以很高的概率落入该波门中。如果有量测点落入波门,则该航迹变为初始航迹;否则,该航迹被撤销。
③由于初始航迹中包含两个点迹,这两个点可以用来初始化无味卡尔曼滤波器(Unscented Kalman Filter,UKF),接下来的关联波门就可以借助UKF来进行设置。
④从第三次扫描开始,采用M/N逻辑进行航迹判别。
⑤如果在第N+2帧,M/N逻辑条件满足,则该航迹变为确认航迹;否则,该航迹将被撤销。
而当下列条件满足时,一条确认航迹被终结:
①在最近的N∗帧数据中,有M∗帧数据找不到与当前航迹的关联点迹;
②目标航迹的不确定性超过了一定的阈值,其中,航迹的不确定性由状态协方差矩阵来度量;
③目标的运动速度达到了一个不可能的值v max。
数据关联的作用是从包含杂波及多个目标的点迹量测中找到属于当前航迹的量测,数据关联过程首先需要确定关联波门。假定在目标量测的预测值 周围,由目标产生的量测服从高斯分布,则椭圆确认波门由式(6.72)给出:
周围,由目标产生的量测服从高斯分布,则椭圆确认波门由式(6.72)给出:
![]()
波门概率由阈值λ确定。确认波门在球坐标系中是椭圆形,当投影到笛卡儿坐标平面时,呈现出类似“香蕉”的形状。
数据关联一般采用基于贝叶斯理论的联合概率数据关联方法(Joint Probability Data Association,JPDA),它通过概率加权的方式关联当前目标的所有确认量测,包括以下步骤:
①首先建立确认矩阵,该矩阵中包含了每一个量测所有可能的来源;确认矩阵依据确认波门来设置,将这些目标分别编号为j=1,…,J;
②基于确认矩阵,JPDA依据如下两条规则建立所有可能的联合关联事件:a.一个量测要么来自一个目标,要么就是虚警;b.一个目标最多只能产生一个量测,假定检测概率为Pd;
③联合事件的概率根据以下假设进行计算:a.在某个目标量测的预测位置周围,由目标产生的量测数据服从高斯分布;b.监测范围内的虚警服从参数为λ的泊松分布,λ表示杂波密度;
④在确认波门内,假设杂波服从非均匀分布;
⑤边缘关联概率(即量测与目标的关联概率)由联合关联概率获得;
⑥目标的状态参数采用边缘概率对UKF的更新状态进行加权平均得到。
数据关联完成后,需要进行目标状态的预测与更新,可借助JPDA-UKF方法来完成。在第k次扫描时,第j个目标的状态更新值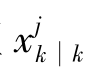 由式(6.73)计算:
由式(6.73)计算:
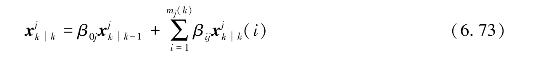
式中,mj(k)表示k时刻第j个目标的确认波门内的量测数目;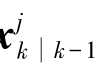 表示k时刻目标状态的预测值;
表示k时刻目标状态的预测值;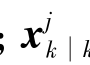 (i)表示利用第i个确认量测得到的UKF更新值;βij表示关联概率:
(i)表示利用第i个确认量测得到的UKF更新值;βij表示关联概率:

状态更新的协方差矩阵由下式计算:
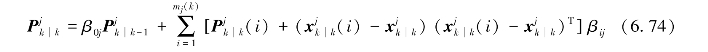
式中,状态预测值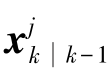 及其协方差矩阵
及其协方差矩阵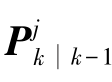 ,目标量测预测值
,目标量测预测值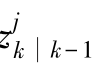 及其协方差矩阵
及其协方差矩阵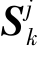 由UKF的预测步骤提供。UKF即无味卡尔曼滤波器,它将经典卡尔曼滤波器的预测-更新循环与无味变换相结合来序贯估计目标的状态参量。与经典卡尔曼滤波方法类似,它也包括预测与更新两个步骤。下面以第j个目标的滤波为例进行描述,假设第i个量测zi,k来自目标。
由UKF的预测步骤提供。UKF即无味卡尔曼滤波器,它将经典卡尔曼滤波器的预测-更新循环与无味变换相结合来序贯估计目标的状态参量。与经典卡尔曼滤波方法类似,它也包括预测与更新两个步骤。下面以第j个目标的滤波为例进行描述,假设第i个量测zi,k来自目标。
3)UKF预测
UKF预测时,首先计算sigma点矩阵:
![]()
具体地,由式(6.75)给出:
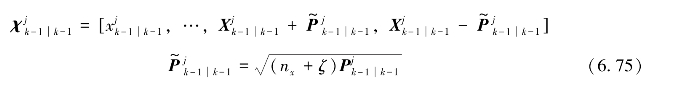
式中,ζ为尺度参数,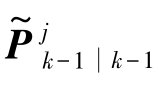 表示尺度化状态协方差矩阵的Cholesky分解,
表示尺度化状态协方差矩阵的Cholesky分解,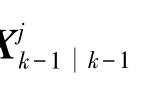 为列向量等于
为列向量等于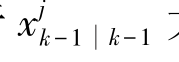 大小为nx×nx的矩阵。通过状态转移方程:
大小为nx×nx的矩阵。通过状态转移方程:
![]()
传递sigma点,然后通过无味权值ωn来预测状态向量:

通过引入状态噪声的协方差矩阵来计算预测状态协方差矩阵:
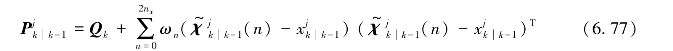
式中,Q k表示状态噪声协方差矩阵。考虑到状态噪声的影响,利用传递状态及状态协方差估计对sigma点重新估计:
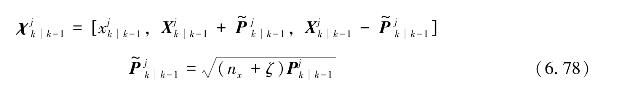
然后,通过观测方程:
![]()
进行传递,对观测向量及其协方差矩阵进行预测:
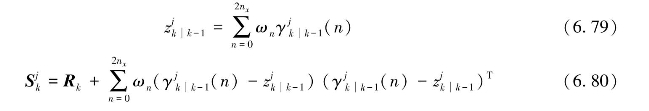
4)UKF更新
一旦接收到第i个量测zk(i),即可计算zk(i)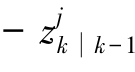 ;然后,利用经典卡尔曼滤波的更新过程对状态向量与状态协方差矩阵进行更新:
;然后,利用经典卡尔曼滤波的更新过程对状态向量与状态协方差矩阵进行更新:

其中,卡尔曼滤波增益由下式计算得到:
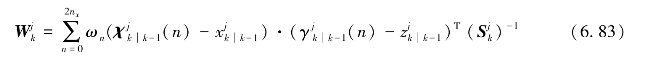
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




