地波雷达海态反演方法：海洋遥感探测技术及应用

本节将介绍高频雷达测量海流、海浪和风场信息的基本原理和典型方法。这三种信息均为矢量信息，即包括幅度和方向。传统上，采用单站地波雷达测量三种海态在径向方向的幅度，利用双站测量另一径向分量后合成为矢量结果。目前存在一些直接利用单站信息合成矢量结果的方法，下面将分别展开介绍。

1.海流监测

（1）地波雷达海流反演原理

目前，地波雷达可以反演流速和流向信息，其中，利用单部雷达可以给出覆盖范围内相对于雷达方向的径向流，利用两部雷达从不同方位观测，可以合成矢量流。单部雷达中海流径向速度的计算，需要雷达一阶谱的偏移量。根据雷达一阶散射截面方程，两对称的一阶峰应该位于Bragg频率位置。当海洋表面存在海流时，海流运载着海浪，会引起一阶散射回波多普勒谱中的两个布拉格尖峰朝同一方向偏移，正负取决于海流流速分量是朝向还是远离雷达运动。图6.3为高频地波雷达海流测量原理示意图。

海流流速在雷达观测方向的径向分量用V cr表示，那么Doppler频率偏移量可以表示为：

这样可以求出海流径向速度为：

（2）基于MUSIC算法的高频雷达海流测向原理

图6.3　高频地波雷达海流测量原理示意图

地波雷达接收的回波谱数据为雷达照射方向的全向回波数据，需要采用测向方法来确定回波的方向，即确定给定海流值所在的方位。目前在海流方位测量中应用较为广泛的方法为多重信号分类法（MUSIC）（Schmidt，1986）。该方法是一种空间谱估计技术，率先应用于CODAR雷达的海流的方位估计，MUSIC算法具有测向精度高、分辨率高等优点。

MUSIC算法的基本思想是将任意阵列输出数据的协方差矩阵进行特征分解，从而得到与信号分量相对应的信号子空间和与信号分量正交的噪声子空间，然后利用这两个子空间的正交性来估计信号源的方位。即信号方位估计问题等效成在阵列流型向量簇a（θ）（θ在雷达波束覆盖的角度范围内取值）中寻找与信号子空间距离最近的向量。a（θ）到信号子空间的欧几里得距离的平方为：

式中，H代表共轭转置，E N为噪声子空间特征向量构成的矩阵。当噪声不存在时，信号方位上的a（θ）落在信号子空间内，上式为零。实际情况中寻找使上式趋于零的θ值，即为信号方位的估计。上式函数的倒数定义为多重信号分类法的方位谱估计，即空间谱函数Pmu（θ）表示为：

连续改变θ值（-90°≤θ≤90°）进行谱峰搜索，当θ等于信号入射角θi时，谱函数出现峰值，即得到信号的入射方向角。

由MUSIC算法可以给出单站径向海流。要获得海流的矢量分布，就必须采用双站或多站多个角度上的海流信息进行合成。如图6.4所示，设P是某一公共网格单元，VC是该单元的矢量流速率，方向为θC（与两雷达连线的夹角），雷达A与探测单元的夹角为θA，探测得到的径向流速为VA，雷达B与探测单元的夹角为θB，探测得到的径向流速为VB，依据下述关系式：

图6.4　雷达获取矢量流示意图

可求出单元P处矢量流的方向和速度分量分别为：

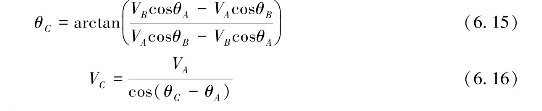
依次求得各公共网格单元上的矢量流，得到公共探测区域内的矢量流场图。

2.海浪监测

根据二阶后向散射原理，雷达电磁波会与不同波长的海浪相互作用，因此二阶回波谱中会包含各种频率海浪的频谱信息（海浪谱），由二阶回波谱的幅度可以得到海面各波长的海浪所占的能量，进而可以给出海表面的有效波高和波向。国际上，从20世纪70年代开始探索利用高频地波雷达探测波浪的相关工作，海浪的反演至今仍是高频地波雷达应用的前沿课题。

雷达二阶后向散射模型为积分方程的形式，由雷达回波谱反演海浪的过程实际上就是求解积分方程的过程，即根据测量的σ（ω）求解S（k）。此类积分求解有多种方式，在此主要介绍三种典型的方法：Howell海浪谱反演法、海浪谱模型反演法和经验海浪谱反演法。

（1）Howell海浪谱反演法

Howell海浪谱反演法为典型的积分方程求解方法，其主要思想为选用不同的基函数对线性化后的积分方程进行求解，得到海浪方向谱。具体为，首先将二阶后向散射表述为如下形式：

将二阶谱除以一阶峰所包含的能量，可得：

线性化处理后可得：

将其进行离散化可得：

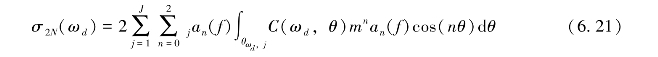
进一步表示为：

对其求广义逆即可得到海浪谱x=C+σ。

（2）海浪谱模型反演方法

Wyatt提出利用模型匹配的方法来测量长波的海浪谱。通过匹配风浪模型，可以将此方法扩展到更高的频率。雷达测量的方向谱可以表示为：

其中，β为常数，θw和α由一阶峰确定，ku是根据风速U得到的波数，a（k），s（k）和θ∗（k）通过模型匹配得到，kc是海浪的阶段频率，kl与雷达频率有关。

（3）经验海浪谱反演方法

此方法是通过学习的方式将雷达测量回波谱与浮标测量海浪谱相关联。在一定海域布置浮标和雷达，设定浮标测量海浪谱和雷达测量二阶回波谱之间的比值为未知量，通过实测波高的学习，确定此比值，之后就可以通过雷达测量二阶谱和比值进行海浪测量。此方法需要进行多种情况训练，且变换探测区域后需重新训练。其基本思路简要介绍如下：将海浪方向谱表示为：

式中，S（ω）为海浪频谱，主要表征不同频率的海浪所具有的能量，即单位频率的能谱密度；F（ω，φ）为方向分布函数，表示组成波的波向分布。而F（ω，φ）最简单的形式是组成波的波向与角频率ω无关，即F（ω，φ）=F（φ）。因此，海浪方向谱一般用式（6.26）表示：

经验法反演海浪方向谱主要通过回归系数法，其基本原理是拟合出高频地波雷达回波谱归一化的二阶截面积与浮标测量海浪方向谱之间的回归系数：

式中，Spk、Smk分别表示一阶峰所对应的正负二阶边带能量；Hk为浮标测量的海浪谱数据；F（φk-φr+π）和F（φk-φr）为方向分布函数，分别对应正负一阶峰所对应的二阶边带；αk为所要求得的回归系数。

在已知海浪频谱数据、方向分布函数（浮标测量）和雷达二阶截面积的前提下，拟合出αk的具体数值。然后使用此数值来求取未布置浮标区域的海浪方向谱，即Hk和φk。

3.海面风向监测

风向的反演主要是基于多普勒谱正负一阶峰的比值和风向的半经验关系。但是，单站高频雷达在反演风向的时候存在180°的风向模糊，为此针对单站高频地波雷达人们发展了一系列的模糊消除方法。主要有以多波束法和多波束思想为基础的一系列方法和最大似然法。这些方法都能够有效地消除单站地波雷达的风向模糊。

风向影响左右一阶海杂波的幅值，因此风向的反演主要是基于正负一阶峰的比值来求解，根据一阶散射截面方程可得：

式中，R为正负一阶峰强度的比值，φ0和φw分别代表波束方向和风向，g代表海浪能量的方向因子模型，其中应用最广泛的是Long-Higgins（1963）提出的模型（通常称为心形函数）：

式中，s为扩散因子，代表海浪能量的分散程度，s越大代表海浪能量越分散，s越小代表海浪能量越集中，φ和φw分别代表海浪方向和风向。将式（6.29）代入到式（6.28）可得：

式中，θ=φw-φ0表示雷达波束与风向间的夹角，由式（6.30）可得：

(www.xing528.com)

1985年，Donelan等（1985）提出了sech模型，即

代入式（6.32）可得：

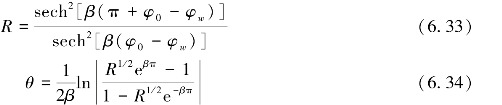
式中，β为扩散因子。风向可表示为：

（1）最小二乘多波束法（LSMB）

在1986年，Heron和Rose（1986）为了消除风向的不确定性，提出了多波束采样的方法。他们假设雷达观测区域内的海浪方向谱是近似均匀分布的，通过不同方向上海洋回波Doppler谱的正负一阶峰比值R的不同，来确定一个合理的风向和方向谱扩散因子。结合式（6.31）和式（6.35），可得到风向角度随扩散因子s的变化曲线，如图6.5（a）所示。当相邻波束具有相同的方向谱扩散因子，即图中有交点，则交点对应的角度即为风向。

图6.5　风向与扩展因子的相关示意图

但是由图6.5（b）可以看出，两列波束有可能没有交点，若利用三列波束，也有可能没有交点或没有共同的交点，根据双站雷达风向反演的方法和多波束的思想采用最小二乘的实现方式（Gurgel等，2006），可以有效解决多波束法没有交点的问题。对于单站雷达，假设风向在相邻区域是一致的，采用双曲正割模型传播函数，则

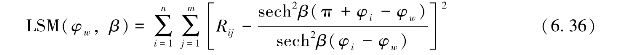
式中，i和j分别代表波束方向和距离元，Rij代表第i个波束方向、第j个距离上的正负一阶峰比值，φi为第i个波束上的角度，φw为风向。该式括号中第一项为实测的正负一阶峰的比值，第二项是由方向因子模型确定的理论的正负一阶峰值。当传播方向因子β∈[0.1　3]变化，φw∈[0　2 π]变化，使上式表达式最小，此时φw的值即为真实的风向值。

可以看出，如果利用传统的波束法直接求交点，若存在交点，式（6.36）中的最小二乘表达式的值必然为零，两者的反演精度相当。若不存在交点，亦可以求最小二乘表达式的最小值，找到一个合理的风向值。图6.6是雷达反演风向与实测数据的比较图。

（2）角度比较多波束法（ACMB）

常规的多波束法会存在多解或无解的情况，Chu（2015）发展了一种新的算法来解决这一问题。为了获得风向，本算法分为两步：一是风向的模糊消除；二是传播因子β的确定。

如图6.7所示，为了获取黑色阴影单元B的实际风向，选择与之相邻的三个单元。当β固定时，利用式（6.34）可以计算得到三个夹角θA、θB和θC。因而，“+”或“-”号可以通过比较θA、θB和θC的大小来确定，具体见表6.4。

图6.6　雷达反演风向与实测数据的比较

图6.7　当θA≤θB＜θC时，风向模糊消除的示意图

表6.4θA、θB和θC的大小与正负号的对应关系

续表

为了确定单元B的β值，需要考虑B单元周围相邻的其他8个单元的风向与波束的夹角。这里β在0.1～3范围内计算，间隔0.1。获得9个单元（包含B单元）的风向之后，对于每个固定的β，可求出9个单元格的方差，如下式所示：

式中，φwi是第i个单元格的风向，是9个单元的平均风向。对于每个β对应一个Δ值，选择最小的方差对应的β值作为B单元的β值，即选择风向均匀性更好的传播因子。那么夹角θB用选择的β求解出来。最终，结合第一步确定的正负号，单元B的风向就可以求出，从而消除了风向模糊。图6.8为ACMB法反演风速与实测风速的比较。

图6.8　ACMB法反演风速与实测风速的比较

（3）最小差值法

在多波束的基础上，武汉大学黄为民（Huang，2004）提出了一种新的消除风向模糊的方法。假设在相邻海域内风向相同或是渐变，那么雷达在该海域相邻的几个雷达元上测得的风向差值之和理应为零或接近零。这里假设该海域有三个雷达面元A，B，C，得到的风向值分别为θA1，θA2，θB1，θB2，θC1，θC2，它们之间的差值为：

式中，i=1，2；j=1，2；k=1，2。当式（6.38）表达式最小所对应的θBj即为雷达元B真实的风向值，由此推出整个雷达区域的风向值。

但是该算法的前提必须是先假定风向扩散因子为常数，一般取值为4。实际情况中，风向扩散因子随着风速变化较大。

（4）最大似然法（ML）

1997年，Wyatt提出了最大似然法来求取风向，最大似然法的核心思想是根据样本值来选取参数，使得样本发生的概率最大。经计算可以得到正负一阶峰比值的概率密度函数。

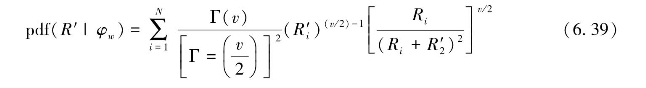
式中，R′为测量值，R为真实值（实际操作中用理论值代替），对于某个单元格，可通过求式（6.39）的最大值来确定风向。

4.风速监测

目前，高频雷达风速反演依然处于研究开发阶段，风速反演方法概括起来主要有根据Barrick经验式反演的波高与风速之间的关系来进行风速反演的经验模型法和神经网络法。

（1）经验模型法反演风速

1982年，Dexter（1982）根据波高和海浪方向谱谱峰频率这两个参数与风速之间的关系（SMB关系式）来进行风速反演，即

式中，g是重力加速度，Hs是有效波高，V10是海面上方10m处风速，fp是峰值频率。上式不宜直接求解，只能采用迭代等方法。利用式（6.40）来反演风速，需要先反演出浪高和峰值频率，而峰值频率是需要通过反演海浪谱来求出的，过程相对繁琐。在国内，文必洋（2001）利用这种方法进行了高频地波雷达风速反演，取得了较好的结果。

李伦等基于SMB关系式建立了海面风速V与有效波高H s的经验模型，风速可表示为：

式中，a和b是待定系数。通过经验模型反演出有效波高，但是利用此模型进行风速反演很大程度上依赖于海面有效波高的反演。

根据Barrick（1977）提出的有效波高的经验模型及Maresca（1980）利用二阶谱能量与一阶谱能量的无权重比值R的推广模型，结合式（6.41）可以得到高频地波雷达海面回波二阶谱能量与一阶谱能量之比和风速关系的双参数模型，即

式（6.42）中，参数a包含了雷达波数k0，a和b仍然为待定系数。由此可见，对于在风作用下充分成长的海面来说，可以不用通过求解Hs，而直接建立比值R与风速的关系，从而对风速进行反演求解。对式（6.42）进行改进，加入第三个参数c以加强拟合曲线的上、下偏移的调节，形成三参数模型，即

利用式（6.43），通过实测数据确定三个参数，从而求解出风速（楚晓亮等，2015）。图6.9为三参数模型反演风速结果与浮标的比较。

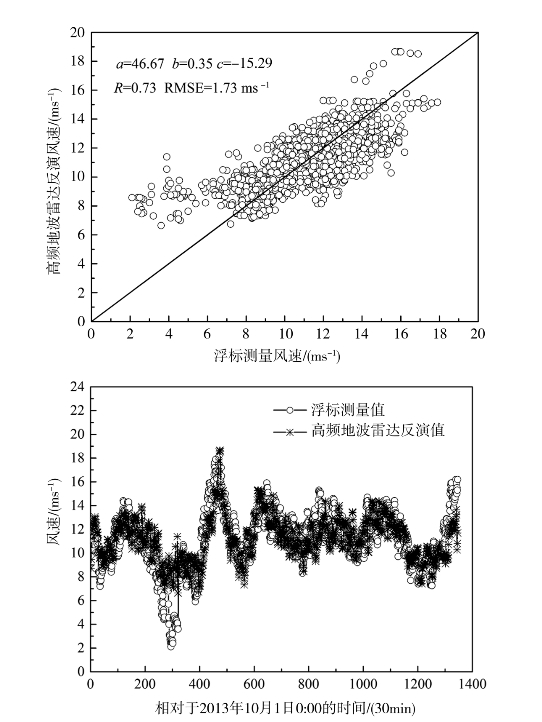
图6.9　三参数模型反演风速结果与浮标比较

（2）神经网络法反演风速

神经网络算法是数学统计方法上的一种应用，通过大量的训练数据，神经网络可以建立输入量与输出量之间的数学模型。Shen等（2012）利用神经网络方法，借助于风向传播函数sech模型，开展风速反演。如前所述，sech模型可表示为：

方向因子β是海浪频率f与峰值频率f p比值的函数，即

若波浪谱为JONSWAP谱，则

式中，F为风区，U10为海面10m高处的风速。将方向因子β与平均波向θB作为神经网络的输入量进行训练可以获得风速。