地波雷达海面回波谱理论-海洋遥感探测技术与应用

高频地波雷达一阶、二阶海面回波的产生机理是Bragg谐振散射。为分析海杂波的产生机理，可以认为海浪是由不同方向和不同波长的理想正弦波叠加而成。高频电磁波与海浪发生相互作用形成电磁波的散射，当入射无线电波波长与海浪波长满足图6.2中所示关系时，反射回波将相干叠加引起最强的散射，即Bragg谐振散射。因为这种谐振效应是由高频电磁波与海浪发生一次作用引起的，所以将此过程称为高频电磁波与海浪的一阶相互作用，由此产生的海面回波信号即为高频地波雷达的一阶Bragg峰。

产生一阶Bragg后向散射的条件为：

式中，L为海浪波长，λ为雷达发射电磁波波长，Δ为发射电磁波的擦地角。对于单站岸基、水平照射的高频地波雷达来说，无线电波擦地角Δ→0，则L=λ/2，即波长等于高频电磁波波长一半的海浪的后向散射回波才满足Bragg谐振散射条件。

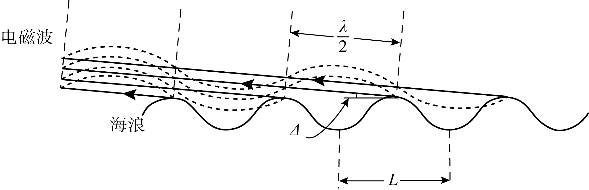
图6.2　一阶Bragg谐振散射机理

在海况充分发展的前提下，由深水行进波色散原理可知，满足一阶Bragg散射条件的海浪的速度（相对于雷达的径向速度）为：

式中，g为重力加速度。具有此特征速度的海浪的后向散射回波的多普勒频率为：

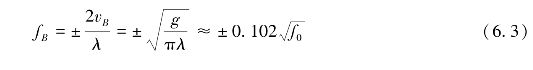
式中，f0为雷达工作频率，单位为MHz，fB为Bragg频率，单位为Hz。式（6.3）中，±号分别代表朝向雷达与背离雷达两个方向的海浪的后向散射回波在回波谱上的多普勒频率。(www.xing528.com)

高频地波雷达的海面回波频谱可以由单位面积内的雷达散射截面积σ（ω）来描述，其中ω为多普勒角频率，单位为rad。在深水中且不存在海水表面流的情况下，由Barrick推导的单站岸基高频地波雷达一阶散射截面积方程为：

式中，k0为雷达电磁波数，ωB为Bragg角频率，m′为多普勒频率的符号，正负分别代表海浪波列行进方向为朝向雷达或背离雷达。由于海浪受多种因素的影响，使海浪具有明显的随机性，以可确定的函数来描述海浪是很困难的。因此，海浪一般使用海浪方向谱来描述，即S（k）为波矢为k的海浪波列的海浪方向谱。

海面回波频谱中不仅包含两个幅度占优的一阶Bragg峰，在一阶谱周围还存在幅度较低的连续频谱，该连续频谱是由高频雷达电磁波与海浪之间发生高阶作用形成的，其中二阶作用产生的二阶海杂波谱较为明显，且具有较为重要的意义。

在深水中且不存在海水表面流的情况下，单站岸基高频地波雷达二阶后向散射截面积方程为：

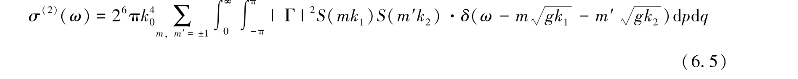
式中，Γ为耦合系数，包含电磁耦合系数ΓEM与流体力学耦合系数ΓH两部分，即

ΓEM和ΓH的计算公式为：

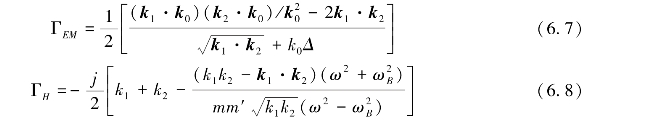
式中，Δ为海洋归一化的海表面阻抗，一般取值为Δ=0.011-j0.012，j为虚数单位；k0是雷达电磁波波数；k1是第一列正弦海浪波列的波矢，k2是第二列正弦海浪波列的波矢，其相应的波数分别为k1和k2；p和q分别表示在海浪波列的波矢平面上建立的直角坐标系的横轴和纵轴，且取p轴与雷达波矢重合；m，m′为多普勒频率的符号，m，m′分别取±1，可表示参与二阶散射作用的两列海浪相互组合的四种情况，而这四种情况实际上对应于岸基高频地波雷达海面回波频谱中二阶海杂波谱的四个区域。