全球海洋初级生产力及黄海POC反演模型

1.初级生产力

海洋初级生产力，是指浮游植物、底栖植物及自养细菌等通过光合作用或化学合成制造有机物的能力，一般用单位时间单位面积所固定的有机碳或能量来表示。海洋初级生产力是海洋生态系统物质和能量循环的基础，对于深刻理解海洋生态系统及其环境特征、海洋生物地球化学循环过程以及海洋在全球气候变化中的作用，均具有重要意义。有研究表明，海洋浮游植物为全球生物圈贡献了近一半的净生产力。因此，研究海洋初级生产力也是实现全球碳循环定量化的一项基本任务。图5.12给出了全球海洋年平均初级生产力的空间分布。

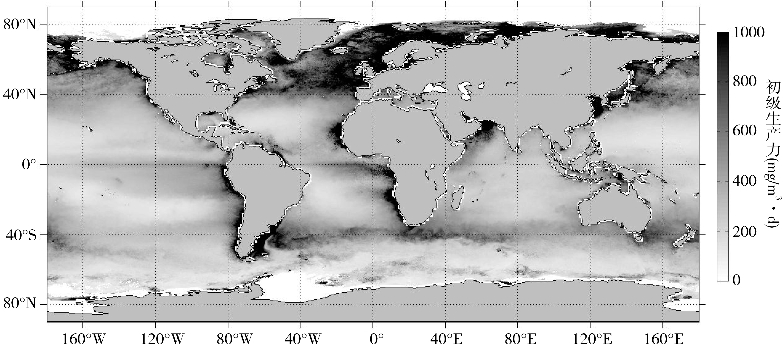
图5.12　2015年全球海洋年平均初级生产力空间分布

在一定的光照条件下，海域初级生产力与叶绿素浓度呈线性相关，这是海洋初级生产力遥感估算的基本原理。基于此原理，研究者在海洋初级生产力估算方面开展了大量的研究工作，目前初级生产力的遥感估算模型大致可分为经验模型和生态学数理模型两类。

经验模型：通过海洋初级生产力与叶绿素浓度以及温度、光照、营养盐等多种因素线性统计关系，来实现初级生产力的估算。1970年，Lorenzen利用表层叶绿素浓度建立了初级生产力的经验模型：

式中，P为海洋初级生产力，单位为g·m-2·d-1；C为表层叶绿素浓度，单位为mg·m-3。1985年，Eppley等（1985）在模型中加入了海表面温度和昼长因子：

式中，P为初级生产力，C为表层叶绿素浓度，T为海表温度，DL为昼长。

经验模型在海洋初级生产力遥感研究的初期应用较为广泛，但随着研究的深入，研究者发现不同海域内的地理环境、气象水文条件、海洋动力过程等不同，导致海洋初级生产力与叶绿素浓度之间的关系存在差异，经验公式的参数需要根据研究海域和时间进行调整，而这种参数的调整往往没有规律可循。另外，遥感反演仅能得到表层的叶绿素浓度，无法得到叶绿素浓度的垂向分布，且两者之间也没有显著的关系，上述不足导致经验模型的精度相当有限，近年来已经较少使用。

生态学数理模型：通过分析海水中光与浮游植物光合作用的响应，找出初级生产力和影响它的各项因子之间的数理关系，属于半经验半理论模型。利用遥感手段获取生态学数理模型中的某些参数，进行相应处理后，用来估算海洋初级生产力，这是目前海洋初级生产力遥感模型的主要技术途径。此类模型中比较有代表性的模型有BPM（Bedford Productivity Model）模型、LPCM（Laboratoire de Physique et Chimie Marines）模型、VGPM（Vertically Generalized Production Model）模型等。

1995年，Longhurst等提出BPM模型，该模型假设叶绿素在垂直方向上均匀分布，光强呈正弦函数分布，模型的公式为：

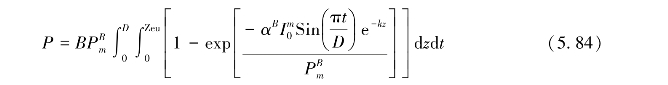
式中，B是叶绿素浓度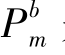，是最大光合作用速率，D为昼长，Z eu是真光层深度，α是由光合作用关系曲线的起始斜率与最大光合作用速率的交点计算得到的光强倒数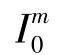，是晴空正午时分的太阳辐射强度，单位为W·m-2，k是海水的光衰减系数。

1996年Antoine等提出LPCM模型，该模型基于每吸收1摩尔光所固定的碳量来计算初级生产力，在计算过程中利用整个水柱的叶绿素浓度代替表层叶绿素浓度。模型公式如下：

式中，JC为光合作用等效能量，CTOT为整个水柱的叶绿素浓度，E0为海面光合有效辐射，Ψ∗为单位重量藻类的光合作用截面，单位是m2/g。

1997年，Behenfeld等基于全球长时间序列的观测数据，发现在初级生产力的计算过程中将叶绿素浓度、光照周期和光学深度归一化后，所有实测初级生产力具有相同形式的垂向分布，由此提出VGPM模型。模型公式为：

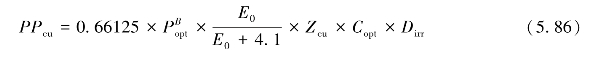(www.xing528.com)

式中，PP eu为表层到真光层的初级生产力，单位为mg·m-2·d-1，表示每天每平方米面积上所产生的碳（毫克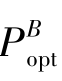）；为水柱的最大固碳速率，单位是mg·mg-1·h-1，表示每小时每毫克叶绿素所固定的碳（毫克）；E0为海面光合有效辐射，单位是mol·m-2·d-1；Z eu为真光层深度，单位是m；C opt为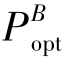处的叶绿素浓度，单位是mg·m-3，可用卫星反演的叶绿素浓度代替；D irr为光照时长，单位为h。

研究表明，即使利用现场实测的叶绿素a浓度作为输入，初级生产力的估算精度最高也仅为50%～60%，倘若利用卫星反演的叶绿素a浓度作为输入，初级生产力的估算精度会更低。

2.透明度

透明度是最基本的海洋水文参数，反映水体的浑浊程度，与海水中悬浮物、叶绿素、黄色物质的含量密切相关，可用于识别水团和流系等。

在透明度半分析反演算法方面，Doron等针对欧洲二类水体发展的透明度反演模型为：

式中，Z SD为水体透明度；ln C0/Ce为常数，表示透明度盘对比度与肉眼观测对比度阈值的比，取值范围是5～10；P是490nm处漫衰减系数Kd（490）与光束衰减系数c（490）的函数，计算公式如下：

K d（490）和c（490）可由水体吸收系数a（490）和后向散射系数b b（490）进行估算，a（490）和b b（490）可通过水体遥感反射率反演得到，因此透明度的反演归结为a（490）和b b（490）的计算。图5.13给出了利用MODIS数据和上述半分析算法反演得到的渤海、黄海透明度分布。

3.颗粒有机碳（POC）

颗粒有机碳是海水中有机颗粒物的碳含量，其中有机颗粒物包含浮游植物、浮游动物细胞及其相应的非生命碎屑、陆源有机颗粒物等。颗粒有机碳是碳在海水中的主要存在形式之一，是海洋碳循环研究中重要的参数，其分布受物理、化学、生物过程等众多因素的影响。

研究表明，POC浓度与海水中悬浮颗粒物的光学后向散射具有较好的相关性。利用这种相关关系结合后向散射系数的反演，可以建立POC反演算法。

作者所在团队基于黄河口海域2011年开展的光学观测实验，建立了该海域的POC反演模型：

实测值与反演值的散点图如图5.14所示，平均相对误差（APD）为25.8%，均方根误差（RMSE）为27mg/m3。

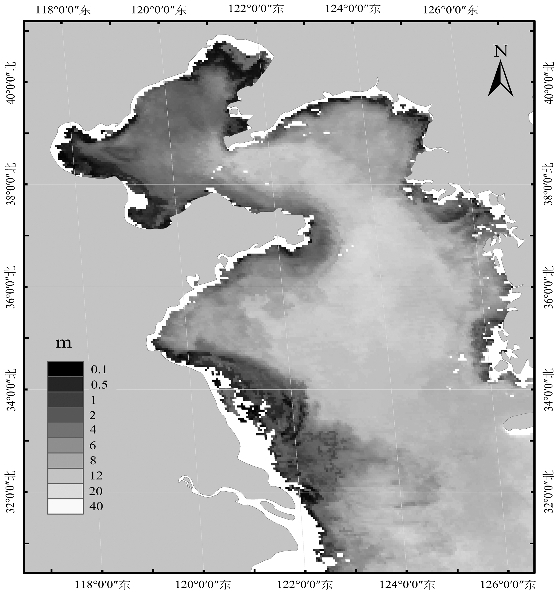
图5.13　2015年3月渤海、黄海透明度分布图

图5.14　黄河口海域POC浓度反演值与实测值的散点图