海洋遥感技术：微波辐射计反演海表温度

微波辐射计能够反演海表温度的机理在于，海表温度通过菲涅耳方程影响海面反射率和发射率，进而改变海表辐射亮温，并通过微波辐射传输方程影响卫星观测亮温。因此，可通过建立相应的反演算法，从微波辐射计亮温数据中提取海表温度信息。

微波辐射计观测亮温主要受到海洋和大气辐射亮温的影响，可由微波辐射传输方程RTE（Radiative Transfer Equation）进行描述：

式中，TBU为大气上行辐射亮温，TBD为大气下行辐射亮温，τ为大气透射率，以上三项可利用大气剖面数据结合大气辐射模型计算；T cos为宇宙背景与天体辐射；TBflat为平静亮温，可由海水介电常数模型计算；TBrough为粗糙海面辐射亮温，其受到辐射计观测角、极化状态、风速、相对风向、风浪谱、泡沫覆盖率等多种参量的共同影响。

由基尔霍夫定律（Kirchhoff Law）可知：如果某介质处于局部热动态平衡条件下，那么其辐射能量的速率和吸收能量的速率相等（刘玉光，2009），可表示为：

式中，e是该介质的发射率（emissivity），a是吸收率（absorptance），λ是电磁波的波长。该公式是基尔霍夫定律最为普适的表达式，该公式既可以应用于某种介质的内部，也可以应用于两种介质的界面处。

由能量守恒定律可知，介质的吸收率a（λ）、反射率r（λ）和透射率t（λ）三者之间存在着守恒关系式：

而对于海洋水体可视为不透明介质，因而有t（λ）≈0，所以有：

用菲涅耳反射率ρ（λ）代替反射率r（λ），由公式（4.2）和公式（4.4）可以得到：

式（4.5）表明，在局部热动态平衡条件下，入射到海面的电磁波能量除了反射的部分以外，所有吸收的能量都将被再次辐射出去。

类似地，对于大气而言，可得大气发射率eA（λ）和大气透射率tA（λ）之和为1，即大气发射率eA（λ）等于1减去大气透射率tA（λ）：

由黑体辐射定律可知，物体微波辐射发射率与其自发辐射辐亮度和相同热力学温度下黑体辐射辐亮度的关系为：

即发射率e（λ，T）为物体自发辐射的辐亮度L（λ，T）和与之具有相同温度T的黑体发射的辐亮度L B（λ，T）之比，则有

普朗克研究了黑体辐射与其热力学温度的关系，通过引入能量量子假设，提出了著名的黑体辐射公式（即普朗克公式）：

式中，λ为电磁波频率，c为真空中的光速，h为普朗克常数，Kb为波尔兹曼常数，L B为黑体辐亮度，T B为黑体热力学温度。微波波段电磁波频率低于300GHz，因此有≪1，此时将普朗克公式取一阶近似有：

因此在微波波段，黑体辐射能力与其热力学温度T成正比。由式（4.8）可知，在相同热力学温度和电磁波波长条件下，包括海洋等在内的地物灰体的辐射能力相当于黑体的e倍（e＜1），因此其辐亮度与黑体辐亮度的比值为：

式（4.11）表明，热力学温度为T的地物，其电磁波辐射能力仅相当于eT（eT＜T）热力学温度下黑体的电磁辐射能力。因此有亮度温度（简称亮温，Brightness Temperature）定义为：

式中，T为地物物理温度，e为地物发射率。针对海洋表面，其发射率为平静海面发射率和粗糙海面发射率之和。海面发射率是观测角、极化状态、温度、盐度、风速、相对风向、风浪谱、泡沫覆盖率等参量的复杂函数。上式是被动微波遥感海气参量的基本公式，其表明与微波辐射计观测数据直接相关的，并不是地物（海面）的物理温度，而是其等效亮度温度。海表发射率受多种海气参量共同影响，因此微波辐射计测量的亮温数据中包含了相应的海气参量信息，可通过亮温敏感性分析，选择对相应海气参量敏感的亮温频段，实现包括SST在内的海气参量信息提取。

由公式（4.5）可知，海表发射率e由反射率ρ决定，而反射率ρ可通过菲涅耳公式计算。由电磁理论可知，电磁波在通过不同介质的交界面时，会发生反射和折射。因此可以使用菲涅耳反射系数（Fresnel reflection coefficient）R来描述反射和入射之间的关系，用菲涅耳透射系数（Fresnel transmission coefficient）T来描述折射与入射之间的关系：

式中，E0i是入射电磁波的电场振幅，E0r是反射电磁波的电场振幅，E0t是透射电磁波的电场振幅，R和T一般是复数。

对于一般弱磁质（如海水），介质的相对磁导率约等于1，根据斯涅耳折射定律（Snell Refraction Law）：

式中，θi表示入射角，θt表示透射角，n′为电磁波的折射率，下标1和2代表着介质1和介质2。

根据电场和磁场在分界面的连续性原理，此时菲涅耳公式有：

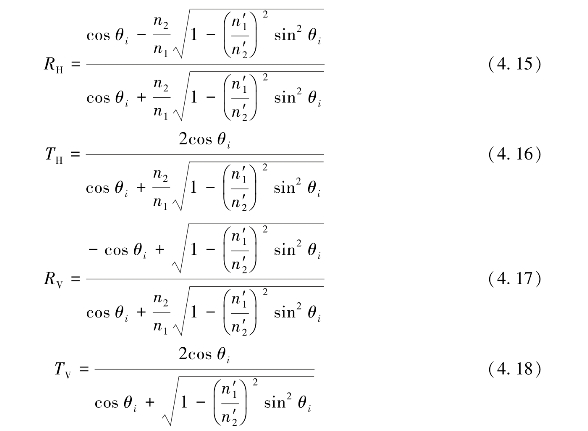
式中，下标“V”和下标“H”分别代表垂直极化和水平极化；复折射率n=n′-in″，其中n′是复折射率的实部，代表电磁波的折射率；n″是复折射率的虚部，代表电磁波的衰减。

复折射率n和相对电容率εr的关系可以表示为：

菲涅耳反射率ρ的定义为反射电磁波的辐亮度和入射电磁波的辐亮度的比值。由于辐亮度和电场振幅绝对值的平方成正比，因此，菲涅耳反射率ρ可以表示成菲涅耳系数R模的平方。因此有平静海面的菲涅耳反射率ρ的表达式为：(www.xing528.com)

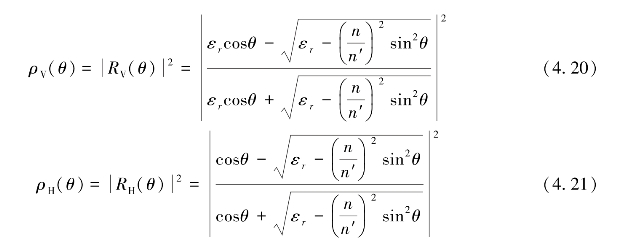
该菲涅耳反射率ρ的公式是普遍适用的公式，可以用于包括微波波段在内的所有电磁波。式中，θ为入射角，εr为介质的复相对电容率（或称为介电常数），可以利用德拜方程（Debye equation）来计算，德拜方程的表达式是：

式中，εr为复相对电容率，无量纲；ω=2πf为电磁波的角频率；T是电介质的温度；S为电介质的盐度；ε∞代表无限高频相对电容率，无量纲；εS代表无静态相对电容率，无量纲；a是经验常数，无量纲；τ是弛豫时间，单位是s；σ是离子电导率；ε0是真空中的电容率，其值是：

德拜方程中各参数的值，一般是通过实验得出的。在频率范围小于10GHz的情况下，Klein和Swift在1977年通过实验测量得到的经验常数a和静态相对电容率εS的公式（Klein，1977）是：

式中系数的计算公式如下：

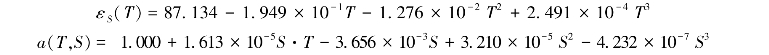
其中，弛豫时间τ的定义是：

式中系数的计算公式如下：

无限高频相对电容率ε∞的取值是：

Stogryn在1972年得出的离子电导率σ的计算公式为（Stogryn，1972）：

式中系数的计算公式如下：

以上公式中T为温度，以℃为单位；S代表盐度，单位是psu（practical salinity unit），30psu=30‰。

Ellison在频率范围为3GHz～89GHz时，得出的经验常数a和静态相对电容率εs的计算公式为（Ellison，1998）：

式中系数的计算公式如下：

其中，弛豫时间τ的计算公式是：

式中系数的计算公式如下：

无限高频相对电容率ε∞的取值是：

式中

离子电导率σ的计算公式为：

公式中的系数的计算公式如下：

以上公式中T为温度，以℃为单位；S代表盐度，单位是psu（practical salinity unit），30psu=30‰。

图4.1是根据Klein-Swift 1977模型计算的0°入射角下、0～40℃范围内平静海面辐射6.9GHz通道亮温。由图4.1可见，该通道亮温基本随SST的变化呈线性变化，有利于SST信息的反演，亮温对SST的敏感度约为0.35K/K。

图4.1　不同海温下的平静海面微波辐射亮温