应用海洋遥感探测技术检测高度计数据重力异常

自1973年测高卫星出现以来，在测高数据的支持下，海洋重力场的确定得到迅速发展。尤其是近20年来，在多代卫星测高计划的支持下，海洋重力场成果丰富。美国加利福尼亚大学圣迭戈分校Scripps海洋研究所（Scripps Institution of Oceanography，SIO）于2005年发布的V15.1模型分辨率达到1′×1′，并于2012年10月5日发布了最新模型V20.1；丹麦科技大学空间研究中心在研制全球平均海平面高模型同时，给出了全球重力异常等系列数据模型，其分辨率达到1′×1′，空间覆盖达到±90°；David Sandwell等（2013）利用CryoSat-2、Envisat和Jason-1大地测量任务等测高数据，提出建立1′×1′且精度为1mGal的全球海洋重力场；我国李建成等（2003）确定了中国近海及邻海2′×2′海洋重力异常模型，其精度在开阔海域达到±3mgal。

利用卫星测高数据反演海洋重力异常的方法主要有：最小二乘配置法、Stokes逆运算法和垂线偏差法等。

最小二乘配置法是利用卫星测高数据确定海洋重力异常的经典方法。Moritz对该理论作了全面深入的介绍，此后，Tscherning、Rapp、Hwang、Rapp和Basic以及Sandwell等对其做了进一步的研究和改进，并有效地利用该方法开展了海洋重力异常反演。最小二乘配置法的优点是可以联合不同类型的重力场参量数据确定重力异常，求解的数值稳定性好，结果平滑。在近海、浅滩区域，将船测重力等资料与海洋测高垂线偏差数据联合，用该方法求解重力异常，能有效降低近海海域卫星回波信号受陆地、岛屿等干扰而造成的海面高误差，进而提高海洋重力异常反演精度。由于需要确定相应的协方差函数和协方差矩阵，运算量大，主要适用于局部小范围计算或开阔海区的计算。

Stokes逆运算法根据Stokes公式的逆运算，将大地水准面起伏恢复成重力异常。该方法可利用FFT计算，不需要全球积分即可快速给出网格型的重力异常，但计算结果可能不稳定，特别是对一些较小的网格。

垂线偏差法是利用垂线偏差反演海洋重力异常的方法。垂线偏差法不仅可以忽略长波误差影响，还可同时采用多颗卫星测高数据，获得较高精度和分辨率的全球重力异常值。该方法目前应用较为广泛，并取得丰富的成果。另外，海洋垂线偏差为大地水准面计算提供了途径，下文以垂线偏差法为例介绍海洋重力异常和大地水准面计算方法。

1.垂线偏差计算方法

计算测高剖面垂线偏差的基本原理是根据测高点测高记录中的位置和时间信息，利用测高数据的一次差分计算测高剖面的数据导数，进而计算海洋上的测高垂线偏差。目前由测高数据计算垂线偏差的方法主要有三种：一是由Sandwell提出的利用测高点的位置和时间信息，求解交叉点处的垂线偏差子午分量和卯酉分量；二是由Olgiati提出的垂线偏差计算方法，首先计算测高卫星地面轨迹的交叉点位置，然后计算交叉点处沿轨方向的垂线偏差，利用交叉点处升轨和降轨沿轨垂线偏差信息，计算交叉点处垂线偏差的子午分量和卯酉分量；三是由Hwang提出的根据测高点的位置信息直接计算沿轨方向的垂线偏差，然后采用最小二乘配置方法直接求解网格点处的垂线偏差子午分量和卯酉分量。

（1）Sandwell方法

Sandwell方法（Sandwell，1992）是由大地水准面对时间的导数和卫星星下点沿轨迹在纬度和经度方向上的速率来计算交叉点上的垂线偏差分量，然后利用拟合内插的方法计算出网格点上的垂线偏差（ξ，η）值，ξ和η分别为垂线偏差的子午分量和卯酉分量。

由卫星测高数据得到的大地水准面高度，分别沿升弧和降弧对时间t求导：

式中，下标a和d分别为升弧和降弧标志，Na表示沿升弧计算点的大地水准面高度对时间的导数，Nd表示沿降弧计算点的大地水准面高度对时间的导数，φ和λ分别为计算点的大地纬度和经度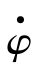，和分别为卫星星下点沿轨迹在纬度和经度方向上的运动速率。

测高卫星的运行轨道近似圆形，因此，在交叉点处，升弧和降弧的经纬度速率存在以下关系：

联合以上各式，解得：

式中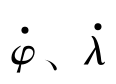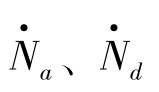，、可由卫星测高记录的时间和位置信息得到。

垂线偏差分量ξ和η与大地水准面高度之间的关系为：

式中，R为平均地球半径。

由此，可得交叉点处垂线偏差分量ξ和η的计算公式为：

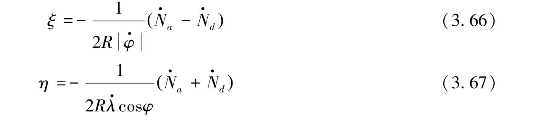
Sandwell垂线偏差计算方法理论严密，在交叉点处计算的垂线偏差精度较高，但该方法仅能计算测高卫星交叉点处的垂线偏差分量（ξ，η），降低了卫星测高资料的空间分辨率，不能满足利用卫星测高资料反演高分辨率海洋重力场的需求。

（2）Olgiati方法

Olgiati方法（Olgiati等，1995）首先计算测高卫星地面轨迹交叉点处沿轨迹方向的垂线偏差ε，然后利用交叉点处升轨和降轨两个沿轨迹垂线偏差，根据下式计算交叉点处垂线偏差的子午分量ξ和卯酉分量η。

式中，εa、εd分别为沿升轨和降轨轨迹方向的垂线偏差，i为测高卫星地面轨迹的倾角，它是星下点纬度和测高卫星轨道倾角I的函数。

如图3.13所示，沿轨迹垂线偏差ε的计算公式为：

式中，d N、d s分别为沿轨迹方向相邻两个观测点之间的大地水准面高度差和距离。

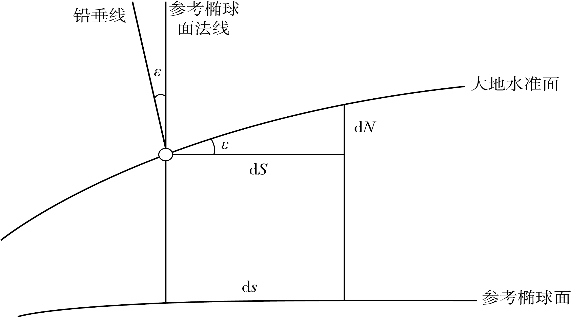
图3.13　垂线偏差与大地水准面高度之间的关系

为了提高测高垂线偏差的空间分辨率，Olgiati根据公式（3.65）计算每条弧上逐个观测点的沿轨迹垂线偏差，利用交叉点处两个沿轨迹方向的垂线偏差推算该点在垂直于轨迹方向的垂线偏差，从而利用交叉点在垂直于轨迹方向的垂线偏差，内插逐个观测点在垂直于轨迹方向的垂线偏差，最后利用每个观测点的沿轨迹垂线偏差和垂直于轨迹方向的垂线偏差联合解算该点的垂线偏差子午分量和卯酉分量。

Olgiati垂线偏差计算方法可以计算每个观测点的垂线偏差分量，提高了空间分辨率，但是，计算过程中需要由交叉点垂线偏差内插出两交叉点之间的观测点在垂直于轨迹方向的垂线偏差，影响了最终垂线偏差子午分量和卯酉分量的反演精度。

（3）Hwang方法

Hwang方法（Hwang等，1998；Hwang等，2002）首先利用测高数据根据公式（3.70）计算各观测点在沿轨迹方向的垂线偏差ε，然后根据观测方程（3.71），直接计算测高垂线偏差子午分量ξ和卯酉分量η在离散格网上的平均值（）。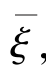

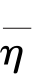沿轨垂线偏差ε与其子午分量ξ和卯酉分量η之间的关系为：

式中，α为测高点沿地面轨迹方向的方位角，如图3.14所示，可以利用相邻测高点的位置信息根据公式（3.72）计算得到。

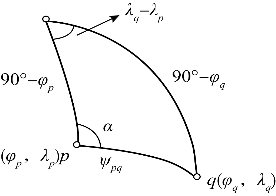
图3.14　点p到点q的方位角α计算示意图

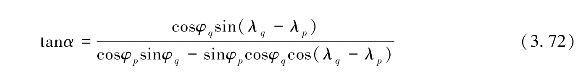
Hwang方法由观测点沿轨垂线偏差ε计算网格点垂线偏差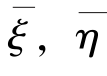（）的观测方程如下：

式中，n为该格网及其邻近海域中沿迹海面高观测点的数目；υi、αi和εi分别为第i个观测点的残差、方位角和沿迹垂线偏差。

将式（3.73）写成矩阵形式：

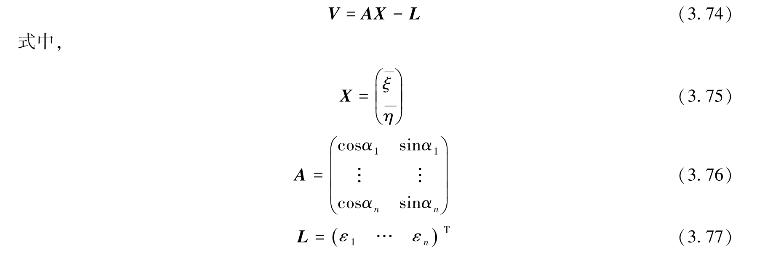
采用间接平差的方法计算，其解为：

其中，P为观测值的权阵。

Hwang垂线偏差方法理论严密，避免了计算测高卫星地面轨迹的交叉点，计算过程简便，提高了网格点垂线偏差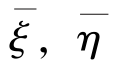（）的空间分辨率和精度。

三种由测高数据反演垂线偏差的方法，Sandwell方法和Olgiati方法得到的垂线偏差结果并不是规则格网结果，还需要采用网格化方法将其内插到规则格网点上，而Hwang垂线偏差计算方法采用沿轨大地水准面梯度直接计算网格点垂线偏差，不需要计算测高卫星地面轨迹的交叉点，并且不需要对海面高度进行交叉点平差，这既能保障反演结果的精度，又对联合应用多颗卫星测高数据来说是一个很大的优势，大大简化了数据处理过程。下面以Hwang垂线偏差计算方法为例给出计算流程如下：

①将测高点海面高观测值减去DOT2008A模型海面地形，得到测高点大地水准面高度；

②移除EGM2008模型大地水准面高度，得到测高点剩余大地水准面高度Nres；

③利用相邻测高点残余大地水准面高度的一次差分对距离的导数，计算测高点剩余沿轨垂线偏差εres；(www.xing528.com)

④根据Hwang垂线偏差计算方法的原理，计算网格点剩余垂线偏差（）；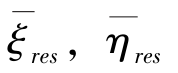

⑤将EGM2008模型垂线偏差与剩余垂线偏差相加，得到最终的垂线偏差计算结果。

2.重力异常计算方法

垂线偏差法是以垂线偏差为观测量，利用逆Vening-Meinesz公式来反演海洋重力异常。由于垂线偏差含有丰富的重力场高频成分，有利于恢复高分辨率海洋重力场，并且垂线偏差是通过测高剖面观测值的一次差分求得，求解过程中削弱了长波误差的影响，比由海面高度反演海洋重力异常结果更稳定，更有利于获得较高精度和分辨率的全球重力异常。

自从1928年Vening Meinesz公布Vening-Meinesz公式以来，由于垂线偏差数据很难广泛地获取，很少有人关注用于将垂线偏差转换为重力异常的逆公式。随着卫星测高技术的发展，获取大范围、高精度、高分辨率的海洋垂线偏差已不再困难，因此，逆Vening-Meinesz公式开始被广泛地用于由卫星测高数据反演海洋重力异常。Hwang于1998年又推导了用于将垂线偏差转换为重力异常和大地水准面高度的逆Vening-Meinesz公式的谱表达方式：

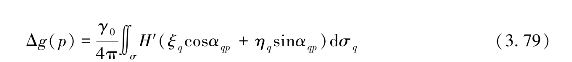
式中，γ0为平均重力，p为计算点，q为流动点，αqp为q点到p点的方位角，ξq和ηq分别为q点垂线偏差的子午分量和卯酉分量，H′为积分核函数的导数。

γ0的计算公式为：

式中，GM为地球引力常数，以T/P卫星参考椭球为基准，GM取值为398600.4415km3/s2，R为地球平均半径。

αqp的计算公式为：

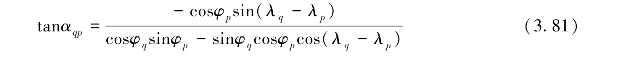
逆Vening-Meinesz公式的关键是确定一个将垂线偏差转换为重力异常的合适的核函数，Hwang给出的核函数表达式为：

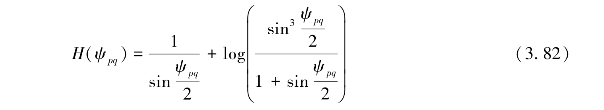
其导数为：

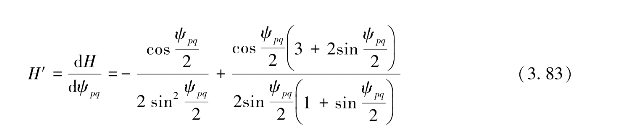
ψpq为p点到q点的球面距离，计算公式如下：

核函数H′的曲线如图3.15所示。

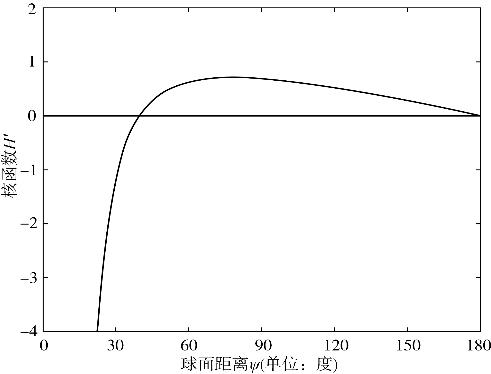
图3.15　核函数H′（ψ）曲线图

由图3.15可以看出，当ψ=43°时，H′=0；当ψ接近0时，H′变化非常快；当ψ很小时，可以用下式代替：

为方便计算，将公式（3.79）转换成累加求和的形式：

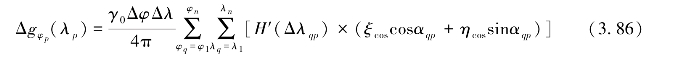
式中，Δφ和Δλ表示网格间距，Δλqp=λq-λp，ξcos=ξq cosφq，ηcos=ηq cosφq。

图3.16为应用上述方法计算得到的中国近海及其邻域2′×2′分辨率重力异常分布图（王莉娟，2012）。

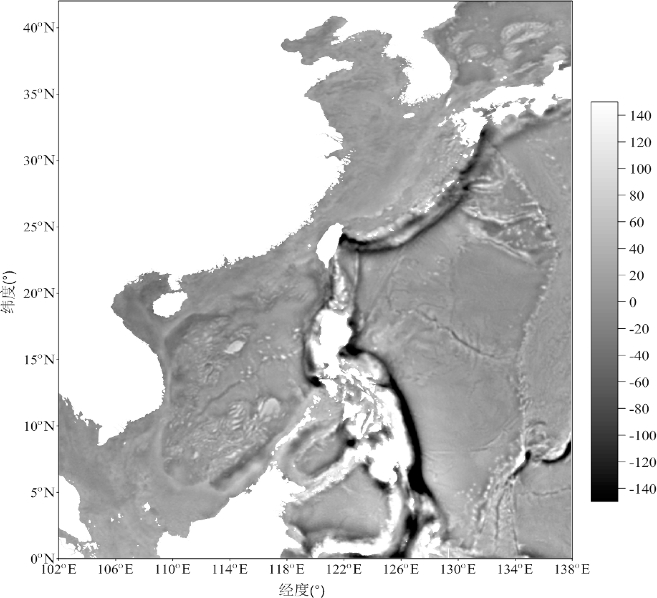
图3.16　中国近海及其邻域重力异常影像图（单位：mGal）

3.大地水准面计算方法

卫星测高的主要任务之一是确定海洋的大地水准面，有如下几种方法：①简单求解法，即从平均海平面中简单扣除海面地形模型的影响，从而得到大地水准面，如Hwang垂线偏差计算方法中的第一个步骤；②联合求解法，即从卫星轨道力学模型和卫星运动方程出发，同时求解卫星的轨道误差、大地水准面误差以及稳态海面地形；③纯几何求解法，即从卫星测高的观测模型出发，求解大地水准面；④垂线偏差法，即利用Molodensky公式由垂线偏差直接反解大地水准面高；⑤最小二乘配置法。各种方法具有不同的优缺点，所得到的大地水准面的精度相差并不大。下面以垂线偏差法为例介绍海洋大地水准面计算方法。

由垂线偏差法计算大地水准面采用Molodensky公式，如下：

式中，ζ为似大地水准面高，即高程异常；σ是单位球面；ψ是计算点P与积分流动点间的球面角距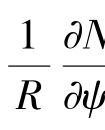，为ψ方向上的垂线偏差分量，且

式中，α是ψ方向上的方位角，亦即计算点P与流动点间的方位角，且

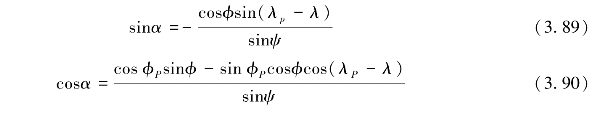
顾及式（3.89）和式（3.90），将式（3.88）代入式（3.87），得

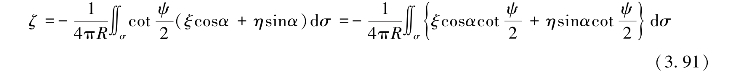
1维卷积表达式可写为：

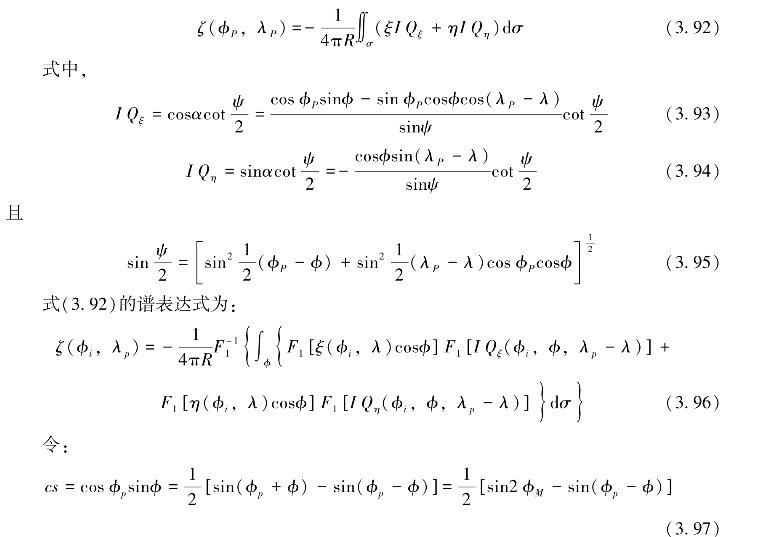
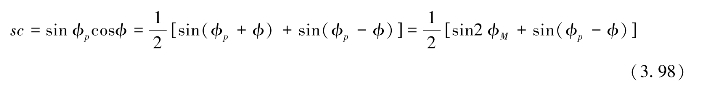
2维球面卷积表达式可写为：

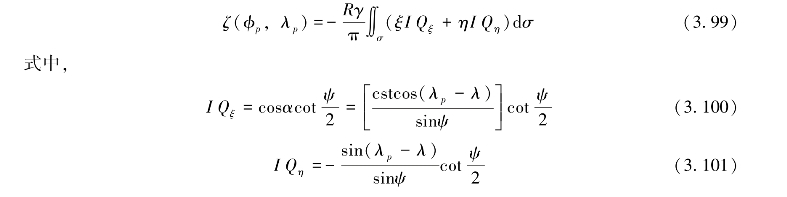
式（3.99）的谱表达式为：

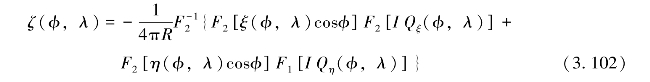
定义一个平面，它以计算点P为原点，X轴指向北极，Y指向东，且X Y平面过P点与大地水准面相切，于是有：

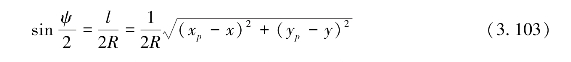
式中，（x，y）和（xp，yp）分别为流动点Q和计算点P的直角坐标。因此，可得

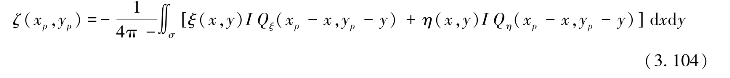
垂线偏差计算似大地水准面用平面坐标表示的2维卷积表达式为：

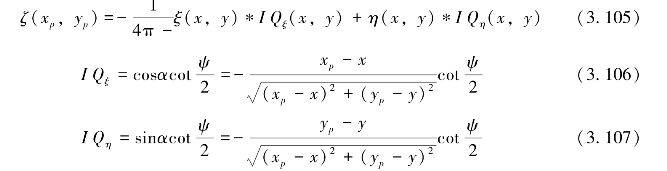
以上从Molodensky的基本公式出发，给出了由垂线偏差的2个分量ξ和η确定高程异常ζ的谱表达式，便于用FFT技术实施快速计算，是由垂线偏差数据计算海洋大地水准面的实用公式。图3.17为利用简单求解法计算得到的中国近海及其邻域大地水准面影像图。

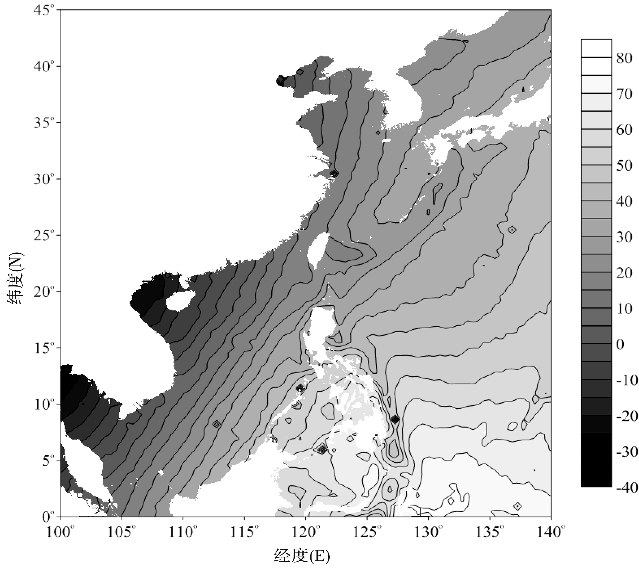
图3.17　中国近海及其邻域大地水准面影像图（单位：cm）