海洋遥感：高度计数据的海浪应用

卫星高度计可获取卫星轨迹星下观测点处的海浪有效波高数据。高度计海浪有效波高数据可用于海浪时空分布与特征分析、谱峰周期分布以及多年一遇极限浪高预测等。

由于高度计观测数据是沿着轨道分布的，且观测时间不同步，利用高度计有效波高开展海浪应用研究时通常需要将时空分布不规则的有效波高数据处理成空间规则分布的网格数据。不过，对于特定区域或特定点的海浪应用研究也可直接采用沿轨有效波高数据。

一般采用反距离加权法进行卫星高度计有效波高数据网格化处理。反距离加权法是目前较为常用的空间插值方法，该方法中观测点离网格点中心越近，其对插值的贡献越大；距离越远，贡献越小。计算公式如下：

式中，Z（xs）为网格点周围第s个观测点的观测值；n为观测点个数；Ws为对应的权重，计算表达式为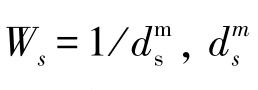是第s个观测点到网格点距离的m次方，常取m=2；Zij为网格点（i，j）处的插值结果。用于网格点处有效波高计算的观测点由数据时空匹配尺度来确定，空间尺度选取为网格数据的空间分辨率，时间尺度选取为网格数据时间分辨率的一半。

利用网格化处理后的时间序列有效波高数据可开展海浪有效波高的月、季和年平均空间分布特征分析，总结海浪有效波高的时空分布与变化规律。图3.3是利用2002年1月至2005年12月Jason-1卫星高度计有效波高数据得到的中国近海海浪有效波高季平均分布图。

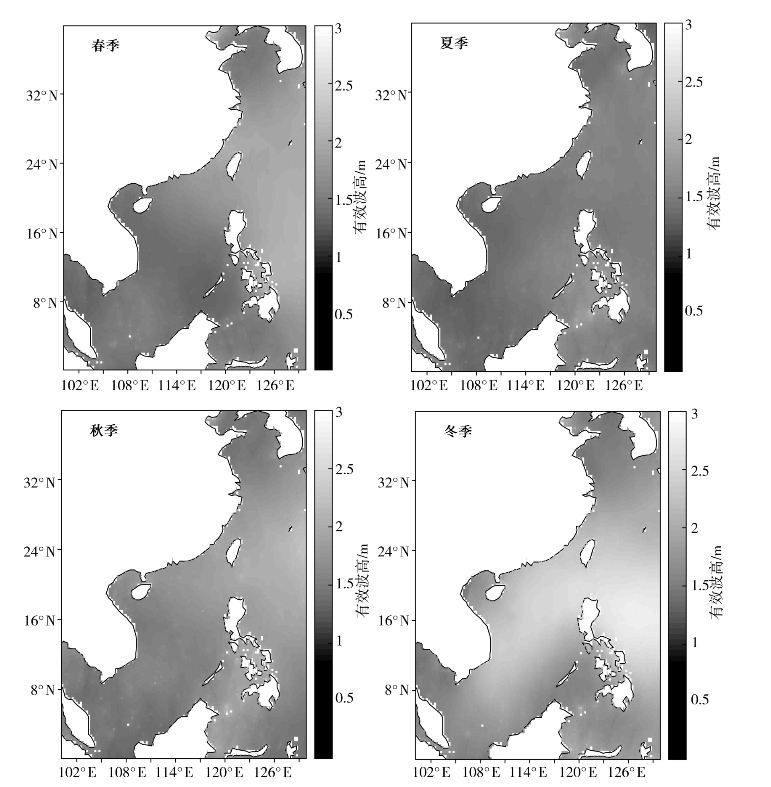
图3.3　基于2015年Jason-2、Cryosat-2和HY-2高度计融合数据的中国近海不同季节海浪有效波高分布图

海浪对海洋工程建筑物安全具有重要影响，该影响主要是由海浪的两个内在特征决定的，即海浪的波高和周期。海浪谱峰周期定义为海浪谱中最大谱值所对应的周期，依据高度计提供的海浪有效波高（SWH）和雷达后向散射截面系数（σ）数据可推算谱峰周期。波浪谱峰周期Tp简单的经验关系式为：

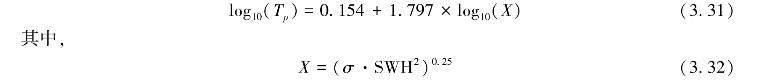
此外，在海洋工程设计中常常需要统计海浪的极值参数。海浪极值推算方法通常采用极值分布理论和适线法，求出海浪在长期内的分布规律，选出一条适合的理论频率曲线，或者通过坐标变换将其化成直线，使其外延以求出多年一遇的极值。三参数Weibull分布法是常用的海浪多年一遇波高极值推算方法之一（方国清，1999；纪永刚等，2002）。(www.xing528.com)

三参数Weibull分布方法利用所选取的观测序列{xi}{yi}来确定三个参数a、b、c，并由其确定Weibull分布。对所选海浪有效波高给定概率y，用以预报x，即分析“多年一遇”问题。Weibull分布的函数形式为：

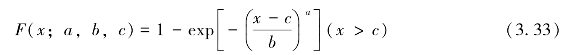
其中，a、b、c分别为形状参数、尺度参数和位置参数。令

设极值重现周期为T，则

变换形式得到：

这样就得到了波高极值x与重现周期T=1/y的函数关系式，然后根据高度计有效波高观测数据来确定三个参数a、b、c的值，进而可推算多年一遇波高极值。

以2002年至2005年共144个周期的Jason-1高度计有效波高观测数据为例，将所有的有效波高数据由大到小排序，选择前n个有效波高值，记为x1，x2，…，xn。这些值对应的y值分别为y1=1/（n+1），y2=2/（n+1），…，yn=n/（n+1），然后利用最小二乘法确定参数a、b、c，进而可以得到函数来计算多年一遇波高极值。