海洋遥感：高效海面风速反演算法

高度计海面风速与后向散射系数σ0之间的物理关系与布拉格散射机理是不同的。入射角较小时后向散射功率几乎全部来自波长为入射波长3倍以上的定向的镜面反射。随着风速的增加，海表面粗糙程度增加，导致更多的入射波的反射方向远离了卫星高度计的方向。因此，σ0与风速近似成反比关系。在入射角较小的情况下，σ0对风向并没有很大的依赖，因此，风速可以从高度计数据中推测出来。后向散射系数与海面风速之间的解析关系式称为“地球物理模式函数”，简称“模式函数”。高度计测量的σ0必须通过模式函数才能转换为海面风速。因此，模式函数的质量直接关系到海面风速的反演精度。

模式函数的选取直接影响卫星高度计风速的反演精度。在高度计发展历程中，风速反演方法大部分都是基于BR经典模式函数，同时针对不同卫星高度计数据的特点进行了改进，其中包括SB、CM、GD、CW以及MCW等模型，在算法发展过程中，逐渐引入了海况的影响因素，其中包括GG、LB以及HD等模型。

目前，卫星高度计使用的风速反演模式函数为改进的MCW模型，模型的输入参数为有效波高与σ0，经过模型中的一系列运算最终求得风速。

（1）风速模型

风速模型公式如下：

(www.xing528.com)

风速模型简写为U10=f（σ0，SWH）。

（2）模型关键参数

模型中的W x、W y、B x、B Y即为系数矩阵，算法采用BP神经网络，利用卫星高度计σ0、有效波高以及风速，经过两层网络拟合，设定的误差限为0.00001，最终得到了模型采用的系数矩阵，如图3.2所示。

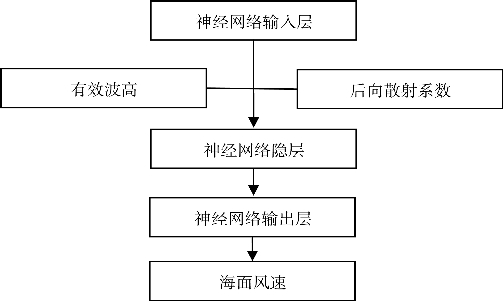
图3.2　基于神经网络获取海面风速反演模型系数矩阵