海洋遥感探测技术提取海面高度

海面高度是卫星雷达高度计提供的主要产品之一，为获取准确的海面高度信息，需要对卫星高度计获取的原始高度进行一系列校正，主要包括干对流层校正、湿对流层校正、电离层校正、海况偏差校正和地球物理调整等，如图3.1所示。

图3.1　测高误差示意图

以下对大气折射校正、海况偏差校正和外部地球物理校正常用算法逐一介绍。

1.干对流层校正

干对流层路径延迟主要是由干燥大气对高度计脉冲信号延迟所导致，是对流层校正的主要部分，其典型值为190～250cm。

干对流层校正采用与海面大气压和星下点纬度有关的模型算法，该算法为目前卫星高度计干对流层校正的通用算法：

式中，PD dry为干对流层校正值，单位为cm，P0为海面大气压（SLP），单位为mbar，φ为星下点地面纬度。

海面大气压数据采用NCEP提供的网格化压强数据，通过时空插值获得与高度计匹配点的数据。

2.湿对流层校正

湿对流层路径延迟是由大气中水汽和云液水对高度计脉冲信号延迟效应导致的，其中水汽修正项为主要部分，典型值为0～50cm；云液水修正项相对较小，通常小于1cm。校正方法有模型法和校正辐射计法。

（1）模型法

湿对流层校正模型算法通过NCEP提供的大气和海面物理参数计算路径延迟量。湿对流层路径延迟包括两部分：水汽导致的路径延迟和云液水导致的路径延迟。水汽导致的路径延迟：

云液水导致的路径延迟：

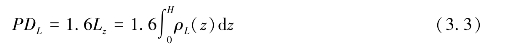
总的湿对流层距离延迟：

式中，PDV，PDL，PDW分别为水汽、云液水和总的路径延迟量，单位为cm。ρV，ρL，T分别为水蒸气、云液水和大气温度的剖面数据，单位分别为g/cm3、g/cm3、K，H为卫星高度，单位为cm。

使用NCEP提供的网格化位势、温度、相对湿度剖面数据和云液水含量数据，通过时空插值得到高度计星下点位置的相应数据。为保证时间上的相关性，选择与卫星过境时间最接近的NCEP数据。

（2）校正辐射计法

校正辐射计法是根据高度计搭载的校正辐射计的各通道亮温值，通过一组反演系数，进行亮温线性组合计算。反演系数通过辐射传输亮温模拟算法和反演系数矩阵研制方法得到，并根据不同的风速和PD值进行分层。

3.电离层校正

电离层路径延迟是由大气中的自由电子对高度计脉冲信号折射所导致的，通常为0.2～40cm。电离层路径延迟校正主要有双频法和模型法。

（1）双频法

主流卫星高度计均工作在Ku和C两个波段，根据两个波段的卫星高度计测高值，获取电离层校正值。计算方法如下：

式中，h Ku、h C分别是Ku波段和C波段的测量值，b Ku、b C为其他与频率相关的误差校正项（如海况偏差）。

对于HY-2A卫星高度计而言，f Ku=13.58GHz、f C=5.25GHz，则K=6.69。

（2）模型法

IRI模型是目前最有效且被广泛认可的电离层经验模型，它融汇了多个大气参数模型，引入了太阳活动和地磁指数的月平均参数，采用预报的电离层特征参数描述电离层剖面。通过IRI模型提供的电子浓度剖面数据计算测量点的总电子含量，进而得到电离层校正值。

总电子含量计算公式为：

电离层校正值可表示为：

式中，f为微波频率。

4.海况偏差校正

海况偏差与海况密切相关，包括电磁偏差、斜偏差和跟踪偏差。电磁偏差是平均散射面和真实的平均海平面之间的不符值。研究发现，实际测量得出的平均散射面略低于真实的平均海表面高度，跟踪器跟踪平均散射面时造成的偏差为斜偏差和跟踪偏差。海况偏差的典型值在-1%和-4%SWH之间。海况偏差的机理比较复杂，在T/P高度计中2m波高时RMS可达2.0cm，而T/P高度计中总RMS仅为4.1cm，可见其在总RMS中所占的比重非常大，已经取代轨道误差成为贡献最大的误差源。理论推导的SSB模型并不适用于高度计的海况偏差校正。一般采用经验模型，常见的有参数模型和非参数模型。

（1）参数模型

参数模型基于SSB与SWH线性相关这一基本假设，则SSB参数模型可写为：(www.xing528.com)

其中，b是一个无量纲的负值，称为海况偏差系数，X是与海况相关的变量组成的向量，θ是参数向量。在以往的经验研究中，X一般直接从高度计测得的与海况相关的变量中选取，即有效波高SWH、风速U或后向散射系数σ0以及它们的组合。由于U和σ0具有高度相关性（通常用σ0反演U），因此，两者只能选其一，本研究选择使用U。将b对SWH和U进行泰勒展开，则可得到如下形式的SSB校正参数模型：

利用高度计交叉点数据建立数据集，通过交叉点处上升轨下降轨对应测量值平差得到海表面高度、有效波高、风速的不符值。采用最小二乘拟合确定参数模型的系数值，以完成建模。参数模型不仅具有表达式简单直观、分析容易以及使用方便的优点，而且具有极佳的外延性。

（2）非参数模型

参数模型建模时采用的不符值导致确定参数模型系数时不是真正的最小二乘拟合。而采用非参数方法不预先设定海况偏差与有效波高和风速变量的具体函数形式，模型结果相比较参数而言精度提高。近年来，非参数模型在国际上得到了广泛的应用，国外的卫星高度计自从Jason-1开始已经逐步采用非参数模型对海况偏差进行估计并校正。非参数模型有核函数估计（NW）、局部线性回归估计（LLR）、K-近邻估计、正交序列估计、多项式样条估计等，带宽分为全局和局部带宽两种。

SSB非参数估计的公式为：

式中，φ（x）是任意测量点海况偏差估计值，x是向量，代表SWH和U。角标1表示交叉点升轨值；角标2表示交叉点降轨值，n为交叉点数据量；yi为交叉点处海表面高度不符值；φ（x1 i）为交叉点升轨处SSB估计值；Wni为基于不同核函数构建的权重矩阵。

由于非参数模型建模过程需要数据集中每一个均与其余所有数据参与计算，计算量特别大，因此在模型应用上往往先计算各个周期的海况偏差，之后建立海况偏差表并采用双线性插值的方法应用，这种应用方法降低了非参数模型的外延性。

5.海洋潮汐校正

海洋潮汐校正主要包括海洋潮与负荷潮。海洋潮汐校正、负荷潮校正主要采用GOT00.2和FES2004模型。根据卫星高度计过境的经纬度和时间信息，通过时空插值可以获得所需测高位置的潮汐校正值。

（1）GOT00.2模型

GOT00.2模型是一种海洋潮汐的经验模型，它是正在运行的Jason-1卫星的潮汐订正模型之一。它应用了T/P的286个10天周期的数据，同时增加了浅海和极地海洋（纬度高于66°）上ERS-1和ERS-2的81个35天周期的数据。该模型的网格为0.5°×0.5°，可用于计算海洋潮汐和负荷潮。

（2）FES2004模型

FES2004模型是一个基于全球有限元网格的水动力系列模型FES的最新版本。该模型是在FES2002水动力模型基础上，同化了验潮站数据和再处理后的T/P、ERS交叉数据后得到的（同化的数据包括671个验潮站、337个T/P和1254个ERS高度计交叉点数据），包含半日分潮M2、S2、N2、K2、2N2和全日分潮K1、O1、Q1、P1，还包含了由纯水动力模型计算的四个水动力长周期分潮Mm、Mf、Mtm和Msqm，非线性的浅水分潮M4分潮以及大气潮S1。计算结果包括海洋潮、负荷潮、平衡长周期潮和非平衡长周期潮。

6.固体潮校正

采用IERS中的固体潮计算模型，IERS采用的固体地球潮模型为：

式中，Δhm代表了月球分量（包括永久形变），ΔhS代表了太阳分量（包括永久形变），Δhe代表了地球分量（包含永久分量）。各个分量可以分别表示为：

式中，h2为二阶Love数，是潮高与引潮位势的比值；Me为地球质量；Mm为月球质量；Ms为太阳质量；Ae为地球平均半径；Dm为地球到月球的距离；Ds为地球到太阳的距离；θm为地心到星下点的连线与地心到月球中心连线的夹角；θs为地心到星下点连线与地心到太阳连线的夹角；ψ为星下点处的地心纬度。

7.极潮校正

极潮是通过极轴运动的离心效应而产生的，通过势能表示如下：

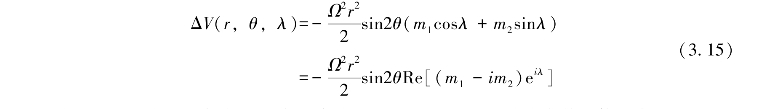
由ΔV导致的径向位移Sr和水平位移Sθ，Sλ可以通过潮汐洛夫数的使用来获得：

式（3.16）中采用洛夫数值（h=0.6027，l=0.0836），同时地球半径r=a=6.378×106m，则式（3.16）可变为：

摆动变量（m1，m2）和极轴运动变量（xp，yp）之间的关系式为：

式中，（xp，yp）为极轴平均位置，它由IERS提供，也可通过线性关系近似出极轴路径。以下估计公式同样由IERS提供：

8.大气逆压校正

大气逆压校正采用一个与海面气压和全球海面平均气压有关的模型方法进行校正，即大气逆压校正量：

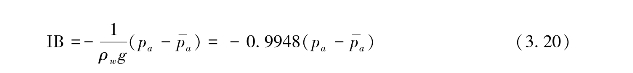
其中，IB的单位为cm；ρw为海水密度，取值1.025g/cm3；g为重力加速度，取值为980.6cm/s2；pa为海面大气压（SLP），单位为mbar；为加权的当前cycle的全球海面平均气压，即=0.5+0.5×1013.3，单位为mbar。

9.高频振荡校正

海面高频振荡主要来源于大气压力动态部分和海面风等。MOG2D-G全球正压模型用于海面高频振荡校正的计算，该模型采用有限元方法进行空间离散，在地形起伏剧烈区域和浅海区适当增加空间分辨率，其有限元网格大小从开阔海域400km到近岸20km不等。动力大气改正（DAC）模型由CLS联合MOG2D-G模型的高频部分（小于20天）得到，其有效时间自1992年起，空间分辨率为0.25°×0.25°，每天提供0：00、6：00、12：00和18：00 4个时间点上的模型计算值，其他时间通过内插得到，现已应用到Jason-1、Envisat以及Jason-2数据中。

海面高频振荡计算采用基于DAC数据插值得到高度计观测点的DAC校正值，然后从DAC值中去除大气逆压校正值（IB）的方法得出。