海洋遥感探测方法：海面风场SAR遥感技术

目前，星载SAR的工作频段包括L波段、S波段、C波段以及X波段，其中，用于海面风场遥感探测的SAR主要工作于C波段和X波段。SAR极化方式包括同极化（VV/HH）和交叉极化（VH/HV），早期SAR的极化方式主要为同极化，并朝着多极化的方向发展。根据不同的工作波段以及不同的极化方式发展了不同的SAR海面风场反演方法。

用于SAR海面风场反演的地球物理模型最早是针对微波散射计发展而来的，在此有必要先介绍微波散射计的海面风场反演方法。

1.微波散射计海面风场反演方法

微波散射计反演海面风场主要包括数据预处理、风矢量反演、质量控制、模糊去除以及数据后处理这五个步骤（钟剑等，2010；Protabella，2002），反演流程如图1.19所示。其中，数据预处理是将卫星观测记录数据转换为归一化后向散射截面（NRCS）；风矢量反演是利用地球物理模型函数将后向散射截面转化为多个模糊风矢量解；模糊去除是从模糊解中选择一个风矢量作为“真实”解的过程；数据后处理是将“真实”风矢量解转换为十进制网格点数据；质量控制是为了去除降雨、冰雪等物理现象所产生的错误风矢量解。其中，风矢量反演和模糊去除是微波散射计海面风场反演的两个难点，下面分别对其进行详细介绍。

图1.19　微波散射计海面风场反演流程

（1）风矢量反演

散射计风矢量反演一般利用地球物理模型函数（Geophysical Model Function，GMF）。地球物理模型函数是指归一化雷达后向散射截面与海面风速、风向、雷达观测参数以及环境参数等之间的定量函数关系。地球物理模型的一般形式为（钟剑等，2010；Protabella，2002）：

公式（1.66）中，σ0为散射计测量的后向散射系数，χ为风向的相对方位角，B0、B1、B2是风速ω、天线入射角θ、散射计工作频率f以及极化方式p的函数，Z对不同的模型取值不同。目前使用较多的地球物理模型函数有C波段的CMOD系列和Ku波段的SASS-1、SASS-2、NSCAT-1、NSCAT-2模型等。其中，CMOD系列已发展到CMOD5，其表达式为（Hersbach等，2007）：

B0、B1、B2是风速ω和入射角θ的函数，B0定义为：

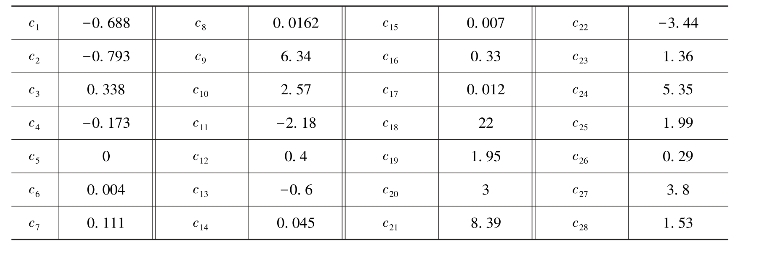
上述公式中系数c是常数，见表1.3，x=（θ-40）/25。数据分析统计表明，CMOD5反演得到的风速相比实际风速具有0.5 m/s的偏差，后又对该模型函数系数进行了一系列订正，建立了CMOD5n等模型函数（Verhoef等，2008）。

表1.3　CMOD5模型函数系数c的值

地球物理模型函数在风场反演中起着关键作用，但它只是一个统计算法，至今还没有被完全认识清楚，并且雷达后向散射截面不是海面风矢量和雷达参数的单值函数，雷达参数也存在误差。所以在实际的风场反演中，采用的是基于统计理论的方法。目前主要有最大似然法MLE、最小平方法LS以及加权最小平方法WLS等。其中，MLE方法具有反演精度高、完全独立于模型函数以及取值范围不受限制等优点，在散射计海面风场反演中应用较广泛（Chi等，1988；林明森等，2013）。MLE目标函数的表达式如下：

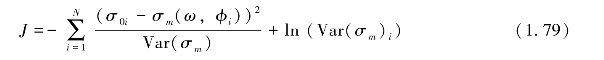
式中，σ0i表示后向散射系数的测量值，σm（ω，ϕi）表示后向散射系数的模型结果，N表示后向散射系数的测量次数，Var（σm）i=α σm 2+βσm+γ=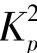（）i为测量偏差，系数α，β，γ与天线与风矢量单元的位置有关。对目标函数求解，通常采用数值方法，在风矢量二维空间内按一定的搜索间隔逐点计算目标函数值并进行比较，寻找局部极值点。

（2）模糊去除

散射计测量的后向散射系数包含噪声的影响，以及模型函数在逆风和顺风观测时具有的各向异性不是很明显，因此通过最大似然估计得到的风矢量解往往不唯一，需从模糊解中选择一个最接近真实解的风矢量作为“真实”风矢量解，即模糊去除。模糊去除的方法主要有FirstRank法、Prescat法和2D-VAR法。其中2D-VAR方法应用较为广泛，其目标函数定义为（钟剑等，2010；Dudley等，2005）：

式中，Jb表示模糊后的风场与背景风场之间的偏差，J scat0表示模糊后的风场与散射计风场之间的偏差。

式中，x=（u，v）表示去模糊后的风场，xb=（ub，vb）表示背景风场，B表示背景风场误差协方差矩阵。上标T表示转置。令δx=（x-xb）=（u′，v′）T，则

采用以下解析形式：

式中，N为模糊解的数目，而

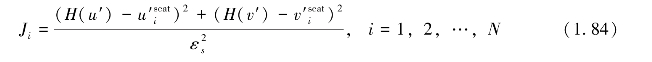
式中，H为观测算子，εs为散射计反演风场的标准偏差。利用上述公式，求取Jb最小时的风矢量解，即为“真实”风矢量解。

2.C波段同极化SAR海面风场反演方法

同极化SAR海面风场反演主要基于地球物理模型函数（GMF）实现。GMF建立了归一化雷达横截面积（Normalized Radar Cross Section，NRCS）与风速、风向、入射角和方位角信息之间的关系。用于C波段同极化SAR风场反演的GMF为CMOD系列模型函数。反演的主要流程如图1.20所示。

图1.20　基于CMOD模型的C波段SAR海面风场反演基本流程图

（1）CMOD模型函数

CMOD模型函数最初是基于C波段VV极化散射计数据发展得到的，但基于SAR和散射计相同的观测海面风场的机理，该模型函数同样适用于C波段VV极化SAR数据并得到了研究验证。常用的CMOD系列模型包括CMOD4、CMOD-IFR2、CMOD5和CMOD5.N模型函数。

1）CMOD4模型

Stoffelen等基于ERS-1散射计数据并利用最大似然估计法（Maximum Likelihood Estimation）计算得到了CMOD4模型函数中的18个系数（Stoffelen等，1997）。该模型中的后向散射系数（σ0）、相对风向（Φ）、风速（V）和卫星波束入射角（θ）的关系如下：

式中，参数F（y），当y＜10-10时，F=0；当10-10≤y≤5时，F=log10 y；当y＞5时，F=/3.2。br是b0的残差校正多项式系数，为θ的函数，其值对应地查找表，见表1.4。

表1.4　CMOD4的残差系数

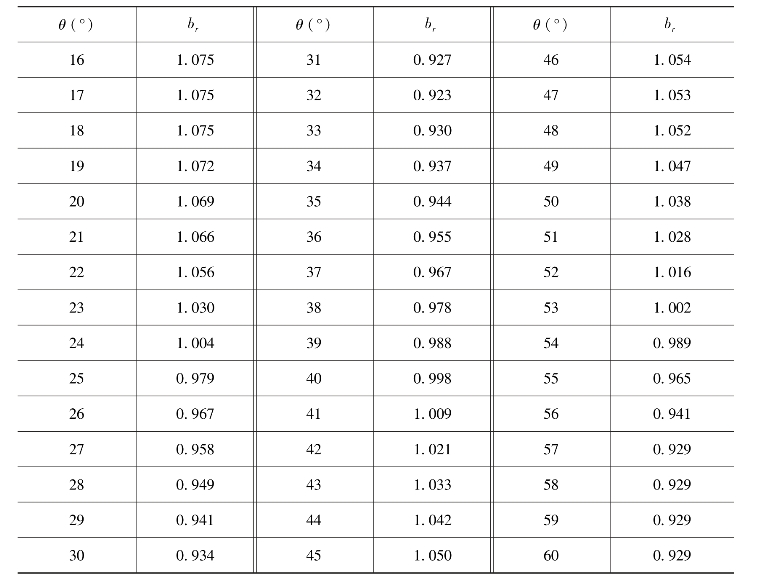
α，β，γ，b1，b2和b3是包含18个系数的勒让德多项式，具体表达如下：

以上勒让德多项式表达式为：

c1，c2，…，c18即为18个勒让德多项式系数，其值见表1.5。

表1.5　CMOD4系数

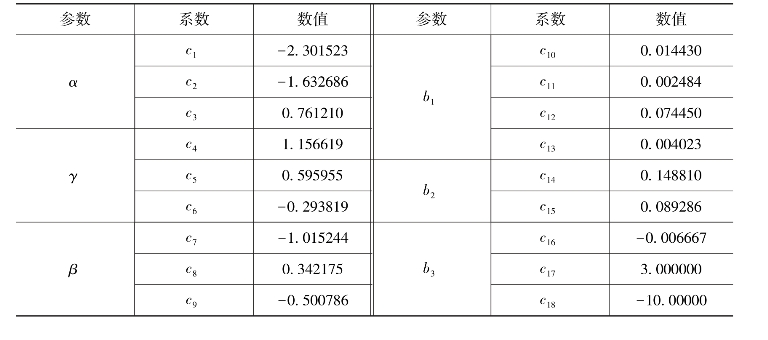
在三维可视化空间里，CMOD4模型函数是一个锥形，在入射角θ=25°时，其模型函数仿真效果如图1.21所示。该模型函数关系式相对简单，但在高风速条件下，由于对σ0存在高估，导致SAR反演风速值明显偏低。

图1.21　CMOD4模型函数中后向散射系数关于风速和相对风向的关系（入射角为25°）

2）CMOD＿IFR2模型

1996年，Vachon和Dobson验证了CMOD＿IFR2模型算法在开阔海域的风速反演精度，结果表明风速反演精度可以达到±1.5m/s左右。CMOD＿IFR2模型函数给出的后向散射系数（σ0）、相对风向（ϕ）、风速（V）和卫星波束入射角（θ）的关系如下（Quilfen等，1998）：

式中，l1=t，l2=（3t2-1）/2，l3=t（5t2-3）/2，t=（θ-36）/19，Q1=y，Q2=2y2-1，y=（2θ-76）/40，V1=（2V-28）/22，V2=2 V21-1，V3=（2V2-1）V1，s1，s2，…，s25是常数，其值见表1.6。

表1.6　CMOD＿IFR2系数

3）CMOD5/CMOD5.N模型

CMOD5模型函数由Hans Hersbach于2003年提出，该模型函数是在CMOD4模型的基础上改进的。CMOD4模型函数在高风速情况下的反演效果不是很理想，经过改进的CMOD5模型函数（Hersbach等，2004；2007），对于高风速的海况有了更好的适用性。

为了获得10m高中性风风速而非真实10m高风风速，需对CMOD5模型反演的风速进行调整。Anton Verhoef等提出调整的方法有两种，一种简单的方法是直接将CMOD5模型反演的风速减去0.7m/s，而另一种更简练的方法则是重新拟合CMOD5模型函数的系数，得到CMOD5.N模型函数（Verhoef等，2008）。因此，CMOD5与CMOD5.N模型函数具有相同的函数形式，主要区别只在于系数的差异。

CMOD5/CMOD5.N模型函数给出的后向散射系数（σ0）、相对风向（ϕ）、风速（V）和卫星波束入射角（θ）的关系如下（Hersbach等，2007）：

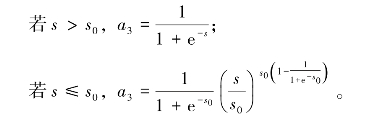(www.xing528.com)

c1，c2，…，c28均是常数，其值见表1.7。

表1.7　CMOD 5和CMOD 5.N系数

（2）风向输入问题

散射计观测海面风场时对同一地点存在多个视向，因此通过多个视向的观测数据结合CMOD模型函数可同时反演海面风速和风向。但SAR不同于散射计，其图像为单一视向，因此无法同时反演风速风向，一般先通过其他方式获取风向，然后再结合CMOD模型函数反演风速。目前，利用CMOD模型反演海面风场时所需的风向输入信息可通过外部辅助数据、数值模型预报数据获取或利用SAR图像本身存在的风条纹信息提取。

1）利用外部辅助数据获取

根据SAR图像获取时间及地理位置，选取相应的散射计数据，然后根据SAR图像的分辨率，对满足时空匹配窗口的风向数据进行插值，得到SAR子图像单元内的风向。

2）利用数值模型预报数据获取

类似利用外部辅助数据获取的方法，根据SAR图像获取时间及地理位置，获取时空匹配的数值模型预报数据，然后再进行时空插值，得到风向信息。

3）利用SAR图像本身存在的风条纹信息提取

该方法需要SAR图像存在大面积的、稳定的风条纹信息，提取的风向信息具有180°模糊，可利用辅助数据去除模糊。常用的从风条纹信息提取风向的方法有以下几种：

局部梯度（LG）法：该方法利用风向与局部梯度方向垂直的原理。首先，对SAR图像进行图像分割，并对得到的子图像单元进行图像平滑，像素大小根据需求可参考设置为100m、200m、400m等，然后计算局部梯度方向；然后对陆地、人工物体等目标进行像素屏蔽，即进行滤波处理；最后，在预先选定的网格单元中选择所有结果方向中最大频率方向为具有180°模糊的风向。

二维FFT变换法：首先对非海面后向散射信息进行屏蔽，即进行滤波处理；然后对SAR图像进行分割，得到SAR子图像，空间分辨率根据需求选择，如10km×10km；再利用平均强度替代屏蔽的像素。最后，进行拟合估计，对SAR子图像进行二维FFT变换，得到的谱能量峰值连线与条纹方向垂直，从而获得具有180°的风向。

小波变换法：首先利用小波变换到小波域，提取风条纹信息；然后利用二维FFT变化计算风条纹的波数谱。二维波数谱的峰值连线的垂线方向即为具有180°的风向。

目前，风向信息的获取是该算法实现的一个难点。上述三种风向获取的方法均存在一定的局限性。第一种方法的主要缺点是散射计数据的空间分辨率相对SAR图像比较粗，且无法提供有效的近岸风向信息；第二种方法虽然可以获取全球的风向信息，但其空间分辨率远低于SAR图像空间分辨率，且其时间分辨率也偏低，通过插值方式获取SAR图像像素元风向时容易引入较大的误差；第三种方法则需要SAR图像存在大面积稳定的风条纹线性特征信息，但统计表明，大约只有43%的SAR图像含有线性特征的风条纹信息，而且利用FFT和LG方法从SAR图像本身风条纹信息反演获取的风向还具有模糊解，仍需要通过其他手段去除。

（3）极化比模型问题

CMOD模型函数只适用C波段VV极化SAR数据，无法直接应用于HH极化SAR数据。利用HH极化SAR数据反演海面风场时需要附加一个将HH极化σ0值转换为对应VV极化σ0值的过程。将HH极化σ0值转换为对应VV极化σ0值的模型即为极化比（Polarization Ratio，PR）模型。将极化比PR定义为VV极化NRCS值与HH极化NRCS值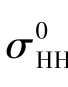的比值，即PR=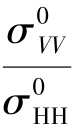。利用不同的SAR图像以及参考数据得到了不同的PR模型，目前比较常用的几个PR模型及其表达式如下：1）Thompson PR模型

Thompson PR模型是Thompson等在1998年提出的PR模型（Thompson等，1998），其表达式为：

式中，θ为入射角，α为经验常系数。不同学者的研究表明，利用不同SAR数据获得的最优α值存在差异，比如Vachon和Dobson利用RADARSAT-1 SAR数据建议α设置为1.2；Horstman利用RADARSAT-1 ScanSAR数据建议α取1；Monaldo比较RADARSAT-1 SAR反演风速和浮标测量数据将α设置为0.6等。Thompson等则利用多个机载散射计观测数据得到α=0.6。当α=0时，模型表达式得到Bragg共振散射理论确定的PR；当α=1时，得到Kirchhoff散射理论确定的PR。

2）Bragg PR模型

正如上面所提到的，将Thompson PR模型表达式中的α设置为0即得到Bragg PR模型。

3）Kirchhoff PR模型

同样，将Thompson PR模型表达式中的α设置为1即得到Kirchhoff PR模型。

4）Elfouhaily PR模型

Elfouhaily在其研究中提出了一个模型（Elfouhaily等，1996），该模型表达式为：

5）Mouche PR模型

Mouche等于2005年提出了两个PR模型（Mouche等，2005）。

模型1同时依赖于入射角和方位角，对于每个入射角，其表达式为：

式中，θ为入射角，ϕ为方位角。系数Ci与三个主向（逆风：ϕ=0 rad；侧风：ϕ=π/2 rad；顺风：ϕ=π rad）相关，其对应表达式分别为：

而对于每个方位方向，PR与入射角的依赖关系则为：

式中，Aϕ、Bϕ和Cϕ为三个系数，可通过最小二乘拟合获得三个主向对应的值。

模型2仅依赖于入射角，其表达式为：

式中，A、B、C为常系数，可通过最小二乘拟合获得。

6）Hwang PR模型

Hwang等于2010年提出了一个依赖于风速和入射角的分析PR模型（Hwang等，2010），该模型表达式为：

式中，θ为入射角，U10为10m高处的风速，而A（θ）表示为：

a（θ）则表示为：

其中，A1、A2、A3以及a1和a2均可通过拟合获得。

总的来说，上述PR模型是基于不同SAR图像数据以及参考数据在不同海况条件下得到的相对较优的模型，因此，各个模型各有优缺点，并没有一个对于任意SAR图像均最优的PR模型。对于具体的SAR图像数据，需要通过大量的反演结果的精度评价才能较好地确定较适合的PR模型。

3.C波段交叉极化SAR海面风场反演方法

随着星载SAR的发展，SAR极化方式从单极化发展到多极化、全极化。由于具有高信噪比的RADARSAT-1/2 SAR的出现以及数据的积累，使得利用交叉极化SAR数据反演风速成为可能。Paris W.Vachon和John Wolfe基于RADARSAT-2精细全极化模式数据以及加拿大业务化浮标数据得到了RADARSAT-2交叉极化SAR数据与浮标风速之间的关系，表明交叉极化SAR数据独立于风向和入射角，只依赖于风速，并依此建立了C波段SAR交叉极化SAR后向散射系数与风速U10之间的经验关系（Vachon等，2011）。该线性关系表达式如下：

基于此经验线性关系，可直接利用反演海面风速。交叉极化SAR数据与海面10m高中性稳定风速之间的线性关系理论上适用于任意模式的交叉极化SAR数据，但由于不同模式以及不同SAR之间的噪底不同，因此式（1.129）所示的经验关系并不能直接应用于其他SAR和RADARSAT-2其他模式的交叉极化SAR数据的海面风速反演。因此，Zhang Biao等基于RADARSAT-2双极化模式VH极化SAR数据以及浮标、H∗Wind和SFMR风速建立了适用于该模式交叉极化后向散射系数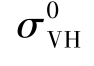与海面风速U10之间的经验关系（Zhang等，2014），其线性表达式为：

4.X波段海面风场反演

与C波段相比，X波段SAR反演风场是较新的应用，同样使用地球物理模型函数（GMF）反演海面风场。目前有学者提出XMOD模型函数用于X波段SAR同极化数据海面风场反演。

Ren等（2012）发展了用于X波段VV极化数据反演海面风速的XMOD1模型函数，该模型函数表达式如下：

其中，U10为海面10m高风速，θ为入射角，φ为相对方位角。利用SIR-X-SAR数据和ECMWF ERA-40风场数据三个调谐数据集估算的系数值见表1.8。

表1.8　三个调谐数据集估算的系数值

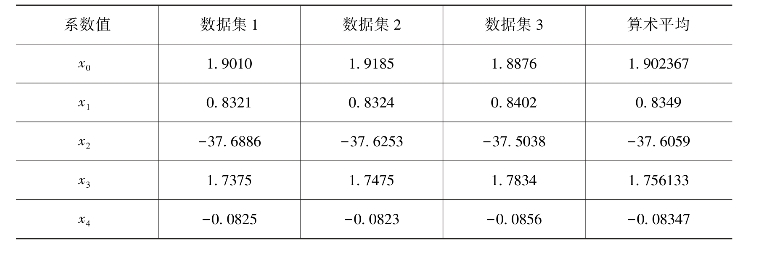
与C波段广泛使用的CMOD4和CMOD5模型函数不同的是XMOD1为海面风速、相对风向和入射角关于X波段VV极化NRCS的线性函数，且假定逆风和顺风条件下NRCS没有差别而忽略了cos（φ）项。

Li和Lehner（2012）提出了一个新的非线性GMF，即XMOD2模型函数，用于TerraSAR-X SAR VV极化数据反演海面风场。模型函数表达式为：

该函数在z空间描述，在d B空间中存在关系d B≡10log（σ0）≡16log（z）。系数B0，B1和B2定义为入射角、10m高风速以及相对风向的函数，其中B0和B2选择为CMOD5相同的函数。B1关于海面风速和入射角的依赖性可表示为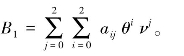

XMOD2模型函数适用于TerraSAR-X VV极化数据，入射角范围为19°～45°，海面风速范围是2～25m/s。