海洋遥感探测方法-海洋遥感探测技术与应用

海浪遥感探测的目的是要获取海浪的统计参数（海浪的有效波高、波周期、波长等），目前的方法主要有两类：一是海浪谱反演方法，首先从SAR图像出发提取海浪二维方向谱，再由海浪二维方向谱的谱矩计算得到海浪的统计参数；二是海浪参数反演的经验方法，即直接由SAR图像提取的信息反演海浪的统计参数。下面详细介绍目前海浪遥感探测的方法。

1.海浪谱反演方法

（1）MPI反演方法

1991年，K.Hasselmann和S.Hasselmann在包含倾斜调制、流体动力学调制和速度聚束调制这三种机制在内的SAR海浪成像机制基础之上，得到了从SAR图像谱反演海浪方向谱的非线性变换。该算法被称为MPI（Max Planck Institute）模式。

MPI方法反演海浪谱需要输入SAR图像谱和第一猜测谱，然后利用前向映射从第一猜测谱计算得到仿真SAR图像谱，再利用仿真的SAR图像谱与观测的SAR图像谱来计算价值函数，接着用价值函数来判断迭代过程是否收敛。MPI模式算法将第一猜测谱引入到价值函数中，在迭代计算中，当价值函数最小时反演得到的海浪谱和猜测谱最接近。

MPI反演算法流程如图1.15所示。

反演算法主要步骤包括：

计算SAR成像调制传递函数：

计算速度聚束调制传递函数：

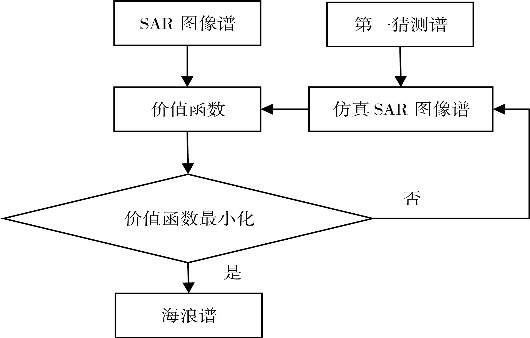
图1.15　MPI反演算法流程

式（1.27）和式（1.28）分别表示观测SAR谱和每次迭代之后的SAR谱之差；初猜海浪谱和每次迭代之后的海浪谱之差。

构造改进的海浪谱

根据改进的海浪谱再次计算改进的仿真SAR谱。经过多次迭代得最适海浪谱和最适SAR谱。

（2）SPRA反演方法

2000年，Mastenbroek和deValk提出了半参数反演方法，它不再需要模式来计算初猜谱，而是加入了与SAR共同配置的散射计所得到的风信息作为附加信息，SPRA的思想就是用经验的含有参数的谱来代替模式计算，谱参数是从SAR图像的信息中提取。所以，SPRA最大的优点在于它不再需要用模式来计算初猜谱，这样就节省了大量的计算时间，也避免了得到的结果依赖于初猜谱。

SPRA反演海浪谱算法流程如图1.16所示。

图1.16　SPRA反演海浪谱算法流程图

SPRA可分为两步进行计算：

第一步：利用散射计所得到的风矢量来构造风浪谱，所含有的待定参数是风浪成长状态以及主波的传播方向，然后含有参数的风浪谱根据非线性的成像关系：

得到仿真SAR谱，然后用搜索法不断变换待定参数的值，直到仿真SAR谱与图像SAR谱的差别最小，那么，此时风浪谱的待定参数确定，从而风浪谱确定。

第二步：风浪谱确定之后，SAR图像谱中除了风浪谱造成的那部分信号，剩余的信号认为是涌浪在SAR图像上的成像，涌浪的成像通常可认为是线性过程，于是SAR的成像关系可以在F=Fws展成泰勒级数，并忽略二次项和高阶项，得

式中，F swell代表涌浪谱。这样，在SAR图像谱Pobs（k），杂乱回波的噪音水平Pcl，以及风浪SAR谱Pws（k）都确定的情况下，涌浪谱就可以求得：

（3）参数化反演方法

1999年，何宜军提出了利用SAR图像谱提取海浪方向谱的参数化方法，该方法克服了由于方位方向的截止造成的信息损失和SAR图像谱180°方向模糊的缺点。

假设参数化海浪方向谱为：？

式中，为平均波向，

选α，ωp，为待求的参数。因为SAR图像谱是由SAR图像经过傅里叶变换产生的，具有180°方向模糊。为了消除180°方向模糊，就必须再提供一个条件。以往一直是利用猜测谱来消除它，但反演结果非常依赖于猜测谱。从一幅SAR图像中选取不同入射角的相邻两块，即在图像距离方向上选取2幅子图像，且假设这两幅子图像对应的海浪方向谱相同。这一假设是符合实际情况的，因此，假设价值函数为：

其中，P1（k），（k），P2（k），2（k）分别为在两不同入射角情况下数值模拟SAR图像谱和观测SAR图像谱。J（α，ωp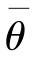，）是相当复杂的函数，利用网格化优化方法求代价函数J 的最小值，得到最优参数α，ωp，，利用它们即可求得海浪方向谱。

（4）交叉谱反演方法

1995年，Engen和Johnsen提出了利用交叉谱反演海浪方向谱的方法，其实现流程如图1.17所示。

该算法对SAR单视复图像进行分视处理，得到子视图像I1、I2，通过对子视图像的交叉相关ρI1，I2做傅里叶变换，则得到两视之间的SAR图像交叉谱：

图1.17　交叉谱反演海浪谱算法流程图

交叉谱和海浪谱之间的非线性变化如下：

该变换与SAR图像谱到海浪方向谱的非线性变换关系完全相同，但是中间函数的定义不同，如下：

可以看到，交叉谱的非线性变换中多了一个指数项exp（iωΔt），此项正好体现了两子视图像之间的时间差Δt。

多视处理时，子视之间的时间间隔的计算公式如下：

其中，λ为雷达波长，R为卫星与目标的距离（斜距），V为平台速度，Δf为各分视的带宽。

式（1.42）的一阶展开则得到海浪谱与SAR图像交叉谱之间的线性变换，如下式：

其中，SAR调制传递函数为RAR调制传递函数与速度聚束效应之和，如下式：

(www.xing528.com)

RAR调制传递函数可认为是三种调制过程的总和，即

其中，倾斜调制传递函数为：

距离聚束调制传递函数为：

水动力学调制传递函数为：

式中，θ（≤60°）为平均雷达入射角，衰减系数μ为松弛系数，取为0.5s，用来描述短波对长波调制的响应。

如果只把式（1.3）的积分项一阶展开而保留指数项，则得到SAR图像交叉谱与海浪谱之间的准线性变换：

利用上式可由SAR图像交叉谱反演得到海浪谱。

（5）PARSA反演方法

2005年，Stellenfleth-Schulz等提出了一种结合利用MPI模式和交叉谱算法的PARSA（Partition Rescaling and Shift Algorithm）算法，该算法是MPI模式的一个改进和扩展，该算法需要海浪数值模式提供第一猜测信息，通常由模式谱提供；另外，采用了谱分割的方法。

PARSA反演海浪谱算法流程如图1.18所示。

反演算法的一个基本要求就是把SAR观测得到的图像谱和模式提供的猜测谱尽量一致地融合在一起，而不是像MPI方法那样强调调整或者修改其中的某一个。因此，基于这个思想，PARSA反演算法的实施基于最大后验概率方法（Rodgers，2001）。反演的思路是在给定SAR图像谱和第一猜测谱的条件下，使得反演得到的海浪谱具有最大的条件概率分布，利用Bayes理论可以得到海浪谱的条件概率分布：

其中，pdf（Φk Fk，α）为观测的交叉谱的条件概率分布，pdf（α）是SAR对海浪成像传输方程中参数的先验概率分布，pdf（Fk）为初猜谱的先验概率分布。

图1.18　PARSA反演海浪谱算法流程图

后验概率最大化的过程实际上就是代价函数最小化的过程。

（6）极化SAR反演方法

随着极化SAR技术的发展，已有部分学者开展了基于极化数据的海浪信息提取研究。2004年，Schuler等首先给出了利用全极化SAR图像进行海浪谱提取的算法，利用极化方向角提取方位向海浪斜率，利用H-Alpha极化分解提取距离向海浪斜率。该方法可以直接测量海浪谱，不需要复杂的调制传递函数，在中低海况下精度较高。

具体的反演方法如下：由于极化Alpha角α仅与距离向局地入射角θr相关，因此可利用SAR数据提供的极化Alpha角α来反演局地入射角θr，并进一步探测距离向倾斜角，从而实现距离向斜率的探测。

根据极化散射原理，极化Alpha角α的计算公式近似为：

根据IEM积分方程，在中高海况下，海表面散射系数σvv和σhh可表示为距离向局地入射角θr、风速U和海表面介电常数ε的函数。将其代入式（1.55）则有：

上式中，风速U可由SAR数据反演得到；极化Alpha角α由极化SAR数据直接提取；海表面介电常数ε可由实测数据求得。将风速U、极化Alpha角α和海表面介电常数ε代入式（1.55），即可求出距离向局地入射角θr。

考虑到距离向的局地入射角θr是雷达视角ϕ和距离向倾斜角γ的差值，则倾斜角γ可表示为：

距离向倾斜角γ、方位向倾斜角ω以及极化方向角θ三者之间的关系可表示为：

其中，ϕ为雷达视角。上式中，距离向倾斜角γ可由式（1.57）得到，极化方向角θ可由圆极化变换得到。将它们代入式（1.58）中即可得到方位向倾斜角ω。

在得到距离向倾斜角γ和方位向倾斜角ω以后，就可以得到距离向和方位向的海表面斜率：S r=tanγ，S r=tanω。

然后，利用小波变换的方法，从极化SAR数据中提取海浪的传播方向φ。由此，海面斜率S rms可表示为：

最后，根据求出的海面斜率S rms即可得到海浪方向谱。

2.海浪参数反演的经验方法

SAR反演海浪谱的过程相对比较复杂，同时需要模式提供初猜谱的信息，其应用受到了一定的限制。近几年，出现了多种海浪参数反演的经验方法，这些方法可以直接利用SAR图像中提取的信息反演海浪参数，不需要反演海浪谱的中间环节，简化了反演的过程，同时也可以获得较高的反演精度。德国宇航中心在此领域开展了大量的研究工作，发展了海浪参数反演的系列参数化方法，目前该方法已被欧空局（ESA）采纳为业务化的算法。

（1）德国宇航中心系列方法

2007年，Sehulz-Stellenfleth等给出了一种海浪参数的经验算法CWAVE，该方法直接从ERS-2 SAR波模式数据中提取海浪参数，不需要计算海浪谱。该算法在中低海况条件下反演结果比较理想，但是在高海况条件下反演得到的有效波高具有比较大的负偏差。2010年，李晓明扩展并改进了该经验算法，提出应用于Envisat ASAR波模式数据的CWAVE＿ENV经验模型，并对CWAVE＿ENV经验模型反演得到的海浪参数进行了详细的比较和印证，并且对于高海况条件下反演结果进行了评估，反演的精度均比较理想。2012年，Bruck和Susanne针对高分辨率TerraSAR-X和Tandem-X数据发展了反演海浪参数的经验算法XWAVE，该算法同样不需要先验信息提供，XWAVE经验模式使用TS-X HH和VV极化的聚束模式和条带模式数据和相应的DWD海浪模式波高的结果拟合得到。海况参数使用同一位置获得的浮标数据进行了验证，波向使用海浪模式的结果进行验证，二维海浪谱与海洋雷达Wamos的结果进行了比较，均具有较好的一致性。

CWAVE是由SAR数据计算海浪参数的一种经验方法，不需要引进任何外部信息就可以直接得到海浪参数，该经验函数的输入参数主要有：波模式图像的雷达后向散射系数、图像方差以及SAR图像方差谱中用一系列正交函数计算得到的20个参数。这些参数的选择是通过逐步回归方法进行筛选的。

SAR图像参数表示为：

一般情况下上式中的ns≤22，则海浪参数可以由上述22个参数的二次多项式表示：

其中，a0，…，ansns为多项式系数，可以表示为向量形式：

相应地，SAR图像参数也表示为向量形式：

其中，nf=0.5（ns2+3ns+2）。下面构造代价函数为：

其中，（w（j），S（j））表示海浪参数的模式结果或实测数据与对应的SAR参数组成的向量对，N表示向量对可以收集到的最大数目。采用逐步回归最小二乘法可以算得多项式系数A，这样海浪参数就可以表示为：

（2）半经验方法

2012年，王贺等提出了一种半经验的算法，该算法可以在没有先验信息的前提下从SAR图像中估计波高。该算法是基于理论的SAR海浪成像机制以及两种周期之间的经验关系建立的。本书分析了提出的模型对雷达入射角及波向的依赖性，对于Envisat ASAR波模式数据而言，该模型可以简化成包含两个输入参数的简化形式，例如，输入参数可以是海浪的截断波长和峰值波长，这些参数可以在没有风浪先验知识的前提下从SAR图像中提取。使用Envisat ASAR波模式数据以及匹配的NDBC浮标测量的结果，对开发的经验算法进行了验证并与Envisat ASAR的二级产品进行了比较。均方根误差和散射指数分别是0.52m和19%。验证的结果表明，对于Envisat ASAR波模式数据而言，建立的算法反演效果较好。