力的投影：正负规则-钢筋工：初级

1.力在直角坐标轴上的投影

在xOy坐标系内，若力F与x轴夹角为α，与y轴夹角为β，如图1-7所示，分别用点A、B表示F的始端和终端。从力F的两端A、B分别向x轴作垂线，两垂足a、b在x轴上所截的线段ab，称为力F在x轴的投影，记作X；向y轴作垂线得线段a′b′，称为力F在y轴上的投影，记作Y。并规定从力的始端的投影点a到终端的投影点b与坐标轴的正向一致时，投影取正号，反之取负号。由图1-7中的几何关系可知，力F在x轴和y轴的投影分别为

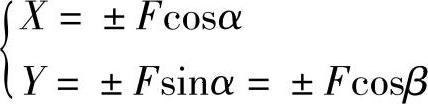
反之，若力F在两个坐标轴上的投影X和Y为已知时，那么也可以求出力F的大小和方向为

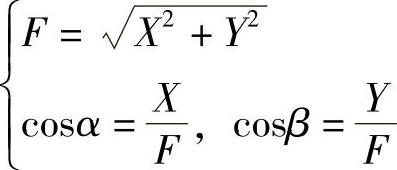
图1-7 力在直角坐标轴上的投影

2.合力投影定理

设由n个力组成的平面汇交力系作用于一个刚体上，如图1-8a所示。以汇交点O作为坐标原点，建立直角坐标系xOy，则将过O点的各汇交力在坐标轴x和y上的投影，记为X_i和Y_i，合力R在x轴和y轴投影为以X和Y表示，它们之间的关系为

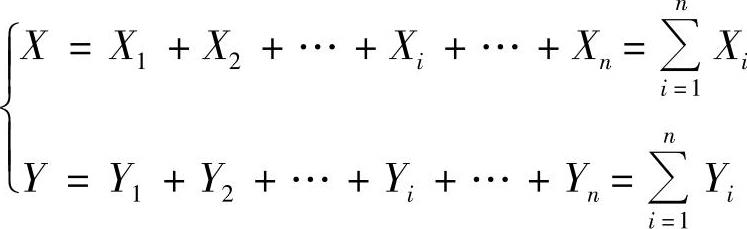
上式表明，合力在某轴上的投影，等于各分力在同一轴上投影的代数和，这就是合力投影定理，如图1-8b所示。

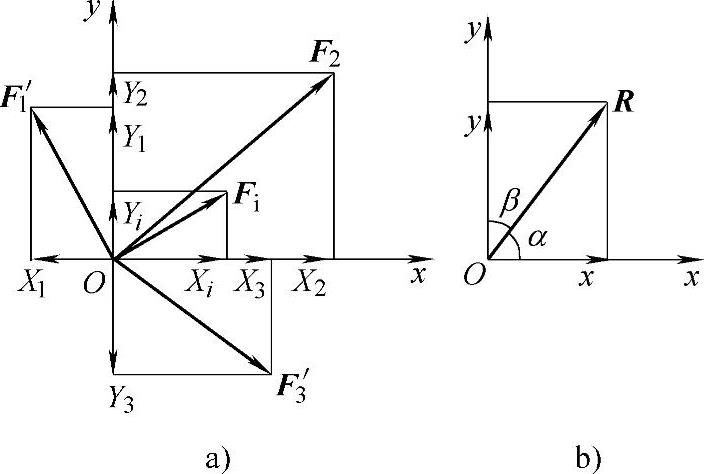
图1-8 合力投影定理

当求得合力在两坐标轴上的投影后，就可以求得合力R的大小和方向为(www.xing528.com)

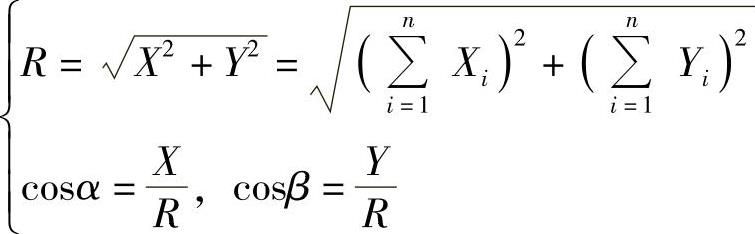
例 求图1-9所示汇交力系合力在x轴的投影。已知：F₁=2kN，F₂=4kN，F₃=5kN，F₄=4kN。

解 各分力在z轴的投影为

X₁=F₁cos0°=2kN×cos0°=2kN

X₂=F₂cos30°=4kN×cos30°=3.46kN

X₃=F₃cos90°=0

X₄=-F₄cos60°=-4kN×cos60°=-2kN

则合力在x轴的投影为

X=X₁+X₂+X₃+X₄=2kN+3.46kN+0+（-2）kN=3.46kN

同理可得到Y=3.54kN。

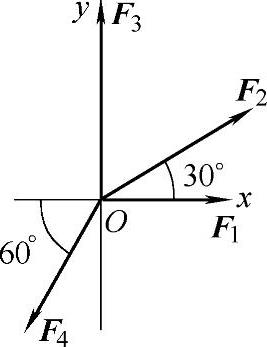
图 1-9