近垂直定向分布的裂缝性地层可等效为HTI介质,具有方位各向异性特征。HTI介质的方位各向异性与裂缝密度、流体填充和岩性等物性参数有关。地震波在不同物性参数组合的裂缝地层中传播的速度大小、极化方向等也不同,则地震反射波振幅和旅行时间也会存在一定的差异。通过研究这种差异,可以反推裂缝地层的裂缝密度、走向和发育带等参数。HTI介质弹性矩阵是连接裂缝参数和地震响应的桥梁,裂缝密度、流体填充和岩性等物性参数直接影响HTI介质的弹性参数,同时弹性参数又决定了地震响应特征。因此HTI介质弹性矩阵构建方法和地震波反射透射特征研究对预测裂缝性储层具有非常现实的意义。
1.HTI介质弹性矩阵构建方法
均匀各向同性介质弹性矩阵C可以由式(5—69)表示,该弹性矩阵只有2个独立参数,即拉梅参数λ和μ。

通过拉梅参数和地层密度ρ可以得到纵波速度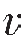 p、横波速度
p、横波速度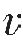 s、泊松比ν、杨氏模量E,体积模量K,剪切模量G等参数,它们之间的关系如式(5—70)所示。
s、泊松比ν、杨氏模量E,体积模量K,剪切模量G等参数,它们之间的关系如式(5—70)所示。
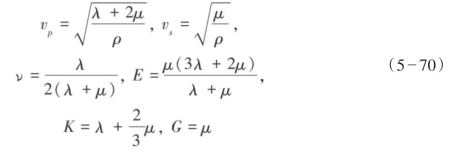
实际情况下较容易通过测井数据得到地层纵波速度、横波速度和密度。根据式(5—70)可以反推拉梅参数得到各向同性介质的弹性矩阵。但是HTI介质的弹性性质由5个相互独立的参数构成,所以必须考虑地层的各向异性来构建HTI介质的弹性矩阵,HTI介质观测系统坐标系下弹性矩阵如式(5—71所示),观测系统坐标系指的是地面是xOy面,z轴是垂直地面向下的坐标系(如图5—36所示)。
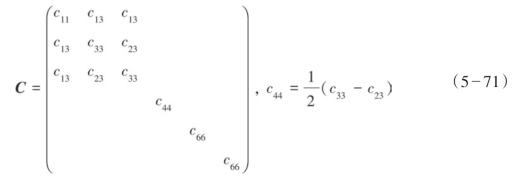
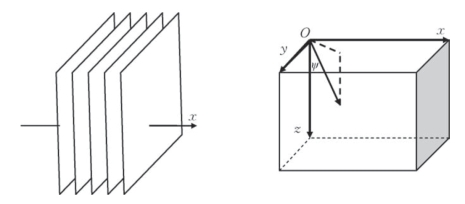
图5—36 HTI介质示意图
为了得到各向异性介质的弹性矩阵,Hudson(1980,1981)、Thomsen(1986,1995)和Schoenberg(1983,1995)都分别提出了各自的理论。
1)Hudson理论
通常认为裂缝存在于各向同性背景介质的包围中,精确求解裂缝介质的弹性矩阵是非常困难的,Hudson给出了几点假设简化了裂缝介质模型。
Hudson假设:① 裂缝是定向排列并且稀疏分布于背景介质中,裂缝尺寸远小于地震波波长;② 裂缝是相互独立的薄扁球体,流体不能在裂缝之间流动,纵横比比较小;③ 裂缝内的气体、液体及其他物质的体积模量和剪切模量都比背景介质小。
在这些假设的基础上,裂缝内的刚度矩阵可以表示为:
![]()
式中,C表示总的模量,C0表示围体的刚度矩阵,C1和C2分别表示裂缝一阶和二阶作用下的弹性矩阵。则式(5—71)表示的HTI介质弹性矩阵的元素可以表示为式(5—73)。
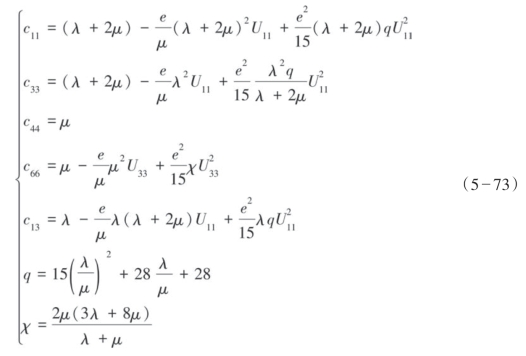
(1)当裂缝为干裂缝时,

(2)当裂缝中填充无黏滞流体时,

(3)当裂缝中填充较小体积模量和剪切模量的固体时,

式中,λ,μ是背景介质的弹性参数;e是裂缝密度;d是裂缝纵横比;λ′,μ′分别为填充介质的拉梅参数。由于Hudson理论假设流体不能在裂缝之间流动,因此该理论仅适合于超声波等高频情况的波场传播,通常意义上说的Hudson理论“低频”效果,指的是裂缝尺寸远小于地震波波长,但并不代表适合于低频波场。
2)Thomsen理论
Hudson没有考虑流体在裂缝之间流动的影响,Thomsen却发展了这一理论,他认为裂缝介质中包含了一套平行的能够连接裂缝与裂缝的粒间孔隙,Thomsen理论的基本假设是流体压力是均衡的。
假设裂缝是便士状并且定向排列、稀疏分布于介质中,那么:

式中,ε、γ、δ分别表示Thomsen弱各向异性参数;Ks是固体颗粒的不可压缩性;Kf是裂缝流体的不可压缩性;ν和E是各向同性孔隙介质(不含裂缝)的泊松比与杨氏模量;ν*和E*是各向同性孔隙介质(不含裂缝)骨架的泊松比与杨氏模量;e代表裂缝密度,可以写成裂缝数目密度Nυ和平均立方直径a的形式,即![]() ,或者可以写成裂缝孔隙度φc和纵横比c/a的形式,c指裂缝厚度,即
,或者可以写成裂缝孔隙度φc和纵横比c/a的形式,c指裂缝厚度,即![]() 。
。
各向同性孔隙介质(不含裂缝)的纵、横波速度可以表示为:
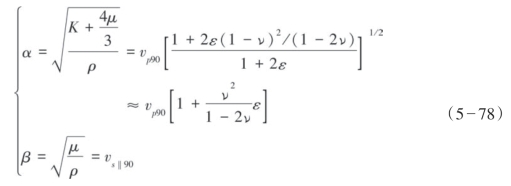
式中,K和μ分别是各向同性背景介质的体积模量和剪切模量;α、β分别表示背景介质不含有裂缝时的纵、横波速度;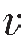 p90、
p90、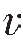 s‖90分别表示背景介质含有裂缝时的各向同性面的纵、横波速度。
s‖90分别表示背景介质含有裂缝时的各向同性面的纵、横波速度。
Dci是流体的影响因素,低频情况下有:
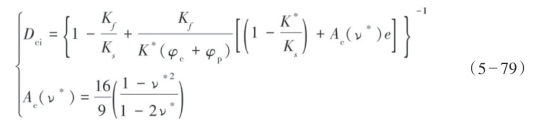
φp是孔隙的孔隙度,中高频情况下有:

Thomsen是在VTI介质本构坐标系下推导各向异性参数的,则对应的HTI介质观测系统坐标系下的弹性矩阵元素可以写成式(5—81)。
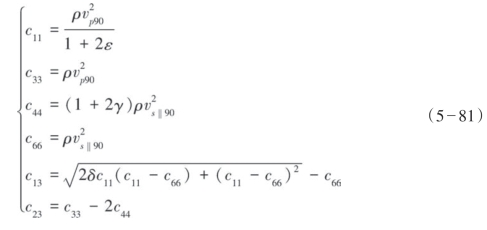
Thomsen理论认为背景介质纵、横波速度是事先已知的,由于测井声波时差和横波时差受到裂缝和各向异性的影响,它们只代表某一方向的裂缝型岩石综合慢度。相比之下,地下岩石矿物成分能够通过测井方法得到,结合Voigt-Reuss-Hill理论可以计算岩石基质等效模量。背景介质骨架由岩石基质和岩石孔隙组成,根据Thomsen理论背景介质孔隙流体低频下可以相互流动,因此可以先利用Kuster-Toksoz理论和岩石基质等效模量计算背景介质骨架等效模量,再用低频Gassmann理论往背景介质孔隙中加入流体得到饱和流体背景介质弹性模量,具体步骤如下。
(1)计算岩石基质弹性模量
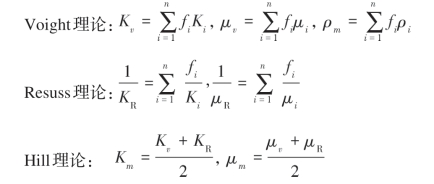
式中,Ki、μi、ρi和fi分别表示第i种固体颗粒的体积模量、剪切模量、密度和体积分数;Kv和μv分别表示Voight理论计算出的岩石基质体积模量和剪切模量;KR和μR分别表示Resuss理论计算出的岩石基质体积模量和剪切模量;Km和μm分别表示Hill理论计算出的岩石基质体积模量和剪切模量;ρm表示岩石基质密度。
(2)计算岩石骨架弹性模量(https://www.xing528.com)
根据Kuster-Toksoz理论,假设岩石孔隙是球体状的,则对于干燥空腔有:
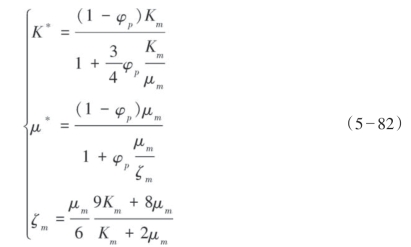
式中,K*和μ*分别表示岩石骨架体积模量和剪切模量。
(3)计算饱和流体岩石弹性模量
根据Gassmann流体理论有:
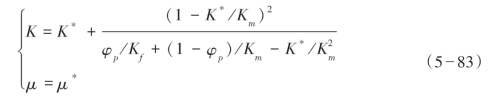
式中,K和μ分别表示饱和流体岩石体积模量和剪切模量,Kf表示流体体积模量。因此结合等效介质理论和Thomsen理论可以构建饱和流体裂缝介质弹性矩阵。
3)Schoenberg理论
Schoenberg的线性滑动理论是把裂缝看作地层中的一个柔性面,此柔性面符合线性滑动的界条件,即上下介质应力连续并且应变差是应力的线性函数。根据Schoenberg和Sayers(1995)的研究,HTI介质的弹性系数矩阵为:
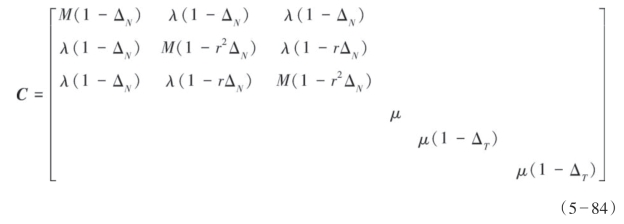
式中,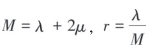 ,λ和μ分别为裂缝所在背景介质的拉梅参数,ΔN和ΔT分别是法向柔度和切向柔度,它们与裂缝充填物有关。Schoenberg理论引入了柔度的概念,但是实际中一般很难直接得到地层柔度,因此只能通过结合Hudson理论和Thomsen理论构建HTI介质弹性矩阵。
,λ和μ分别为裂缝所在背景介质的拉梅参数,ΔN和ΔT分别是法向柔度和切向柔度,它们与裂缝充填物有关。Schoenberg理论引入了柔度的概念,但是实际中一般很难直接得到地层柔度,因此只能通过结合Hudson理论和Thomsen理论构建HTI介质弹性矩阵。
4)三种理论之间关系
(1)Hudson理论和Schoenberg理论
Bakulin(2000)认为Hudson理论和Schoenberg理论研究的是同一种裂缝介质,因此它们的弹性矩阵应该是一致的,通过比较得到:
① 当裂缝为干裂缝时,
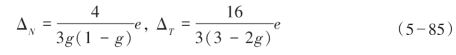
② 当裂缝中填充无黏滞流体时,
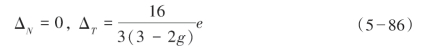
③ 当裂缝中填充较小体积模量和剪切模量的固体时,
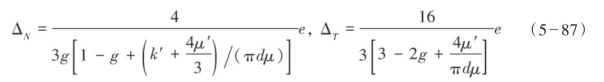
式中,![]() ,k′和μ′分别为填充介质的体积模量和剪切模量,e和d分别为裂缝密度和裂缝的纵横比。可以看出裂缝中无论是否含有流体,切向柔量都没有变化而法向柔量有变化,因此可以通过切向柔量计算裂缝密度,用法向柔量与切向柔量之比进行流体识别。
,k′和μ′分别为填充介质的体积模量和剪切模量,e和d分别为裂缝密度和裂缝的纵横比。可以看出裂缝中无论是否含有流体,切向柔量都没有变化而法向柔量有变化,因此可以通过切向柔量计算裂缝密度,用法向柔量与切向柔量之比进行流体识别。
(2)Schoenberg理论和Thomsen理论
Thomsen的弱各向异性参数是在VTI介质本构坐标系下表示的,Ruger(1996)按照同样的观测系统针对HTI介质提出了新的弱各向异性表达式。
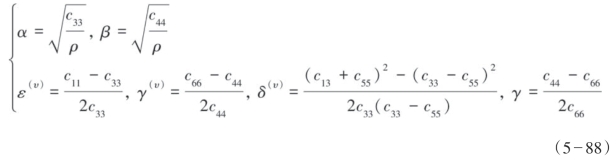
Bakulin把Schoenberg理论的HTI介质弹性矩阵代入上述表达式并且进行线性近似得到:
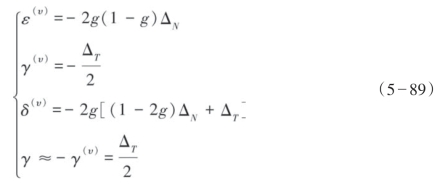
这里把裂缝参数表示的ΔN和ΔT代入弱各向异性参数得到:
① 当裂缝为干裂缝时,
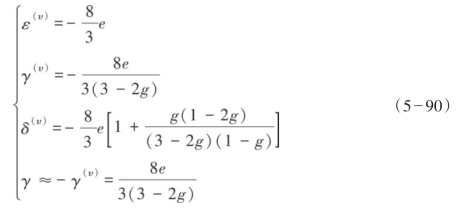
② 当裂缝中包含无黏滞流体时,
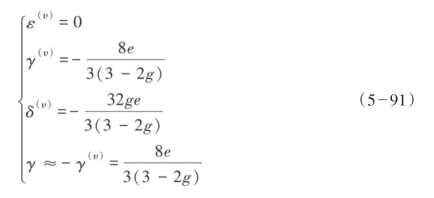
可以发现当裂缝只含气(干裂缝)和裂缝包含流体时,γ(υ)的表达式不变,这就说明它只与裂缝密度有关。这个过程中ε(υ)和δ(υ)发生变化,因此可以用这两个参数来识别流体。
2.HTI介质方位反射系数近似公式
通过构建HTI介质弹性矩阵可以建立裂缝密度、纵横比和填充流体等物性参数与地层弹性参数之间的联系,并且地层弹性参数决定了地震波的传播特征。因此可以通过研究HTI介质地震波传播特征来预测裂缝型储层。为了实现各向异性参数反演,要对精确的HTI方位反射系数公式进行近似化处理。Ruger(1996)、Vavrycuk和Psencik(1998)分别给出了HTI介质P—P波反射系数的近似公式。
1)Ruger近似公式
Ruger(1996)根据一阶扰动理论给出了上下HTI介质对称轴一致的反射系数近似公式:

式中,Z=ρ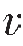 P和ΔZ分别表示上下介质纵波阻抗均值和差异;
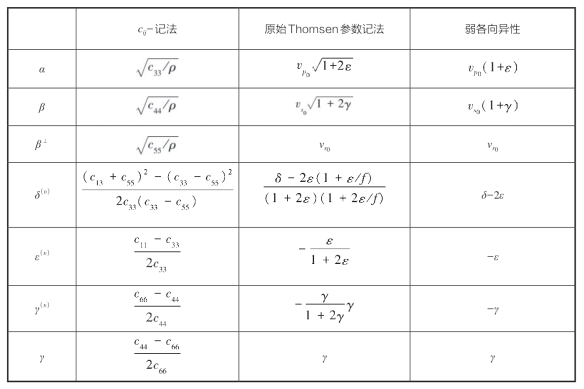
P和ΔZ分别表示上下介质纵波阻抗均值和差异;![]() 和ΔG分别表示上下介质剪切模量均值和差异;α和Δα分别表示上下介质纵波速度均值和差异;β表示上下介质横波速度均值;Δδ(υ),Δγ,Δε(υ)分别表示上下介质各向异性参数差值;θ表示入射角;φ表示方位角,指的是测线方向与HTI介质对称轴方向夹角。Ruger的各向异性参数和Thomsen各向异性参数的关系如表5—1所示,其中f=
和ΔG分别表示上下介质剪切模量均值和差异;α和Δα分别表示上下介质纵波速度均值和差异;β表示上下介质横波速度均值;Δδ(υ),Δγ,Δε(υ)分别表示上下介质各向异性参数差值;θ表示入射角;φ表示方位角,指的是测线方向与HTI介质对称轴方向夹角。Ruger的各向异性参数和Thomsen各向异性参数的关系如表5—1所示,其中f=![]() 。
。
表5—1 各向异性参数表达式
2) Vavrycuk-Psencik近似公式
Vavrycuk和Psencik(1998)推出了如式(5—93)所示的上下HTI介质对称轴方向一致的P-P波反射系数近似公式:

Ruger近似公式和Vavrycuk-Psencik近似公式最大的区别在于二次项的不同。当地震波在裂缝走向方向传播时,Ruger近似解退化为各向同性形式的近似解,反射系数与入射角、上下介质密度、裂缝走向纵波速度、对称轴方向横波速度、对称轴方向剪切模量有关,但是Vavrycuk-Psencik的近似解与入射角、上下介质密度、裂缝走向纵波速度、裂缝走向横波速度、裂缝走向剪切模量以及横波分裂参数γ有关。根据朱兆林等(2005)的研究表明,Ruger近似公式在大方位角、小入射角的情况下精度相对比较高,Vavrycuk-Psencik近似公式在小方位角、大入射角的情况下精度相对比较高。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




