裂缝地层应力场地震岩石物理理论的影响

地应力是存在于地壳中的未受工程扰动的天然应力，它包括由地热、重力、地球自转速度变化及其他因素产生的应力。油气勘探开发中，一般指钻井、油气开采等活动进行之前，地层中地应力原始的大小，又可称为原地应力。

闭合应力是水力压裂工程中的一个分析参数，指示地层裂缝在没有支撑剂时裂缝有效闭合的压力。在地应力的现场测量中，闭合应力诱导水力裂缝关闭时的压力被假定等于最小水平应力。最小水平应力可以表示为σhmin或者σx，最大水平应力可以表示为σHmax或者σy，垂直应力可以表示为σv或者σz。同样，εx和εy表示水平应变，εz表示垂直应变。

1.裂缝地层本构参数定量表征

泊松比描述纵向应变与横向应变之间的关系，杨氏模量是根据胡克定律获得的弹性形变。泊松比和杨氏模量可用下式表示。

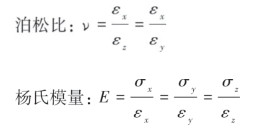
从地震数据估算主应力时，必须意识到会涉及胡克定律中的弹性参数。胡克定律表达了关于弹性应变与应力之间的一个基本关系，并控制水力压裂。也就是说，通过对岩石施加液压会导致岩石产生变形（应变）和出现裂缝。应力与应变的关系由岩石的弹性性质决定。当处于三维应力状态时，胡克定律的广义形式可以转化为含有应变ε随应力σ变化的形式。也就是说，地层的应变ε是其应力σ与有效弹性柔度张量S乘积的函数。

使用常规的6×6简化矩阵符号。式（5—34）可表示为

其中，11→1，22→2，33→3，23→4，13→5，12→6。

根据Schoenberg和Sayers（1995）提出的线性滑动理论，当地层中有垂直裂缝和微裂缝存在时，地层的有效柔度张量可以写成岩石骨架的柔度张量Sb和岩石中微裂缝的柔度张量Sf之和。围岩柔度张量Sb是弹性围岩的柔度。剩余柔度张量Sf可以研究每组平行或是对齐的裂缝。根据Schoenberg和Sayers的理论，有效弹性柔度张量S可以写成：

式中，S为裂缝性地层有效的柔度张量，Sb为围岩柔度张量，Sf为剩余裂缝柔度张量。

因此，运用Schoenberg和Sayers的理论就可将柔度矩阵简化为Sb+Sf，胡克定律也可以做如下简化：

其中，11→1，22→2，33→3，23→4，13→5，12→6。

根据Schoenberg和Sayers的理论，剩余裂缝柔度张量Sf可以写为：

式中，ZN为裂缝面的法向柔度张量，ZT为裂缝面的切向柔度张量。

根据线性滑动理论，裂缝相对于垂直于断裂面的轴线旋转被假定是不变的，并且围岩是各向同性的。因此，通过由ZN所给的法向柔性张量和ZT所给的切向柔性张量可知，全部的柔性张量仅仅决定于两个裂缝柔性张量ZN和ZT。

围岩柔度张量Sb或弹性围岩柔度张量可以由杨氏模量和泊松比表述为：

式中，E为围岩的杨氏模量，ν为围岩的泊松比，μ为围岩的剪切模量（刚性模量）。

单组各向同性围岩介质的旋转不变的裂缝的有效柔度矩阵是围岩柔度矩阵和剩余柔度矩阵的总和。此外，围岩介质可以是垂直横向各向同性（VTI）或相对低对称性的。有效柔度矩阵可以写为：

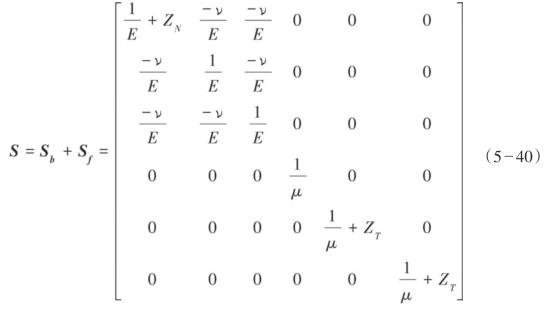
如上所述，线性滑动理论假定一个“单组各向同性围岩介质的旋转不变的裂缝，介质为横向各向同性（TI），其对称轴垂直于裂缝”。换言之，地层被建模为具有水平对称轴的横向各向同性（HTI）介质，或方位各向异性介质。如果可获得足够且合适的可确定其弹性参数的数据，更复杂的各向异性模型也可以用来确定这些参数。换句话说，表示胡克定律式（5—35）的矩阵可写为

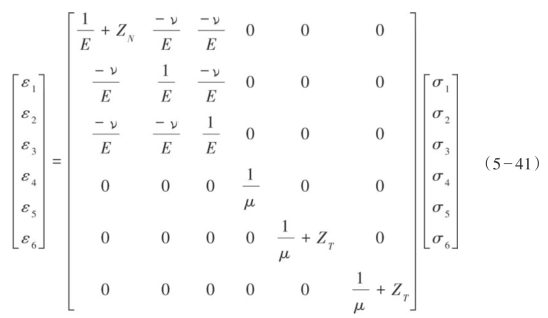
当致力于三维应力状态时，刚度张量C必须结合应力张量σ和应变张量ε定义：

式中，εi为缝隙性地层的应变张量；σj为地层所受的应力张量；Cij为地层的刚度张量。

此外，式（5—43）表明了刚度张量C和柔度矩阵S之间的关系。

因此，通过对式（5—40）的转置，矩阵C可以由柔度矩阵S获取。根据Schoenberg和Sayers的理论，柔度矩阵的转置可以写为：

式中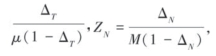，ΔN＝法向弱度，ΔT＝切向弱度。

2.裂缝地层地应力参数与本构参数之间关系的定量表征

正如上面所讨论的，由式（5—42）所给的关系，地层所受的应力可以依据刚性矩阵C写成如下方程：

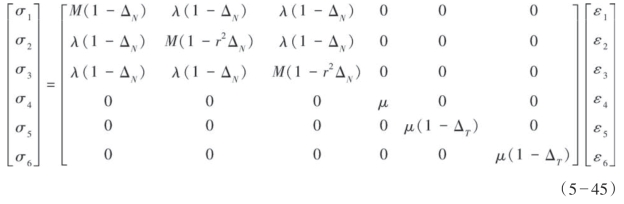
此外，根据Iverson（1995）理论，水平应力σx、σy与垂直应力σz相关，可表示为：

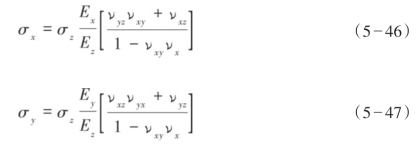
式中，νxy＝εx/εy，νxz＝εx/εz，νyz＝εy/εz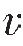，yx＝εy/εx，Ex＝σx/εx，Ey＝σy/εy和Ez＝σz/εz。此外，应变εi可由矩阵式（5—41）计算。例如，水平应变x方向分量可写成：

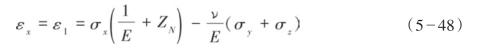
和

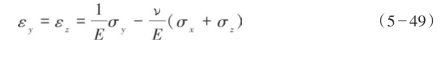
通过Iverson理论所揭示的岩石各向异性性质，意味着假定水平应力不相等，并且假设地下岩石是受约束的，即它们是不动的，此时所有的应变（εx，εy，εz）等于零，式（5—48）的各向异性形式可以写成：

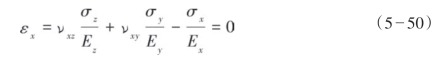
根据Iverson理论，求解式（5—50）得到σy并代入等效公式中求解y方向的应变，得到式（5—51）：

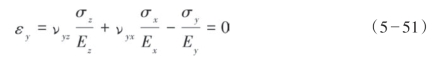(www.xing528.com)

显然，式（5—48）等价于式（5—50），式（5—49）等价于式（5—51）。因此，运用Schoenberg和Sayers的符号和HTI介质的假设，相比之下，Iverson理论中的泊松比与杨氏模量的关系就可以被描述为：

和

也就是说，运用Schoenberg和Sayers假设，Iverson方程式（5—50）中的每个参数可以与对应式（5—48）中的参数相等价。即，

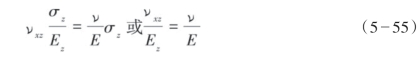
式（5—50）可写为：

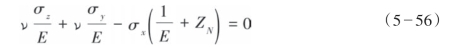
所以

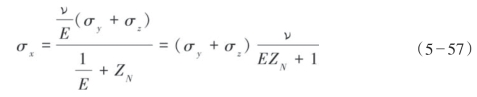
同样地，Schoenberg和Sayers假设可以应用于Iverson方程式（5—51）求解y方向的水平应力，它可以表述为：

将式（5—58）代入式（5—57）中，最后可得到σx关于σz的方程为：

同样地，可得到σy关于σz的方程：

因为可以从地震数据或测井曲线中估算垂直应力σz或运用常规三维地震数据的方位速度和方位AVO反演获得其他参数，所以可以从式（5—59）和式（5—60）中估算出最小水平应力σx和最大水平应力σy。

垂直应力συ或σz可以通过对密度进行积分获得，典型的地层密度可以通过测井得到，也可以利用岩心的密度或地震叠前反演得到。密度的单位用kg/m3，重力加速度g＝9.8 g/m2，两者相乘转化为帕斯卡Pa（kg/ms2），再除以百万转化为兆帕斯卡（MPa）。因此，垂直应力可表示为：

式中，z为深度，g为重力加速度，ρ（h）为深度h处的密度，συ（z）为深度z处的垂直应力。

然后，对式（5—61）随深度近似求和，得到：

所以

因此，结合式（5—62）和式（5—63），并假设测井曲线中或来自地震数据的第一密度值是表面密度，垂直应力可表示为：

式中，是深度为z（i）处的平均密度。

还可以从时域地震数据估算垂直应力。因为地震波旅行时是双程旅行时，并且地震波速度是间隔深度的平均速度，所以式（5—61）可近似于：

间隔深度可近似于：

式中，z为深度；g为重力加速度；ρ（h）为深度h处的密度；συ（z）为深度z处的垂直应力；p为地震波速度，m/s；Δt为地震波双程旅行时，s。

此外，可以应用式（5—59）和式（5—60）以及从式（5—64）或式（5—65）中获得的垂直应力从地震数据中计算应力差分σx-σy。因此，应力差分可表述为

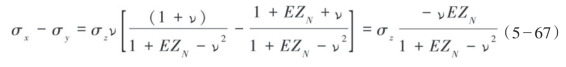
根据式（5—59）和式（5—60）所得的最大水平应力和最小水平应力的差分比或水平应力差分比DHSR（Differential Horizontal Stress Ratio）可描述为：

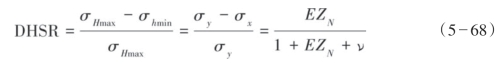
3.裂缝地层地应力指示因子分析及地层应力实现流程

针对前文的地层应力场及水平应力差异的定量表征参数，需要分析这些参数与水力压裂对页岩储层的改造效果的关系。DHSR是决定储层在水力压裂改造下如何成缝的重要参数，DHSR值较大，水力压裂产生的人工裂缝往往与最大水平应力方向平行，成非交错的裂缝平面（如图5—33（b）所示）；相反，当DHSR值较小时，水力压裂能够在多个方向上产生裂缝，成交错裂缝网格（如图5—33（d）所示）。多方向的裂缝网格能够为页岩气提供更有效的运移通道。

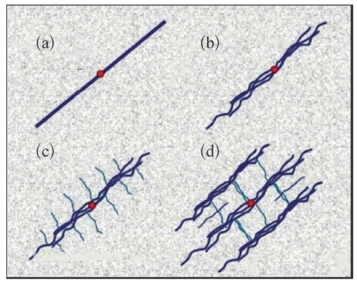
图5—33　水力压裂产生不同类型的人工裂缝

（a）简单裂缝；（b）定向排列复杂裂缝；（c）较大裂缝中存在开启的小裂缝；（d）复杂成网裂缝

储层压裂效果评价要综合其他地层弹性参数才能够指示岩石脆性，如Rickman等（2008）结合杨氏模量和泊松比定义了岩石的脆性指数。Gray等（2012）的研究表明DHSR值与地层是否可压裂成网密切相关，低DHSR值表明此区域的岩石易于出现断裂网络。同样地，高杨氏模量值也表明此区域的地层更易于断裂。因此，最优水力压裂区域将有高杨氏模量值和低DHSR值（如图5—34所示）。

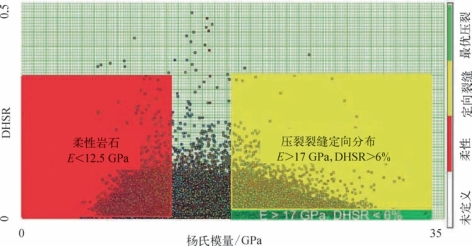
图5—34　杨氏模量与DHSR叠合（Gray等，2012）

以本小节建立的地层应力场地震岩石物理定量表征关系为基础，通过叠前各向异性弹性参数反演，可得到关键参数预测应力场及水平应力变化率。图5—35展示了利用宽方位地震数据进行应力场预测的流程图，这里最关键的就是如何通过各向异性弹性参数反演获得最大、最小水平主应力。

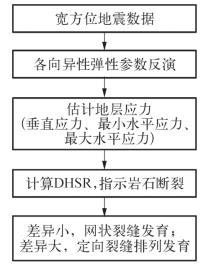
图5—35　地层应力预测的实现流程