脆性指数直接反演-页岩气地震勘探技术

虽然工程上习惯使用E和σ评价页岩脆性，但是地震叠前反演的输出结果通常是纵横波阻抗等参数。弹性参数之间的关系如下：

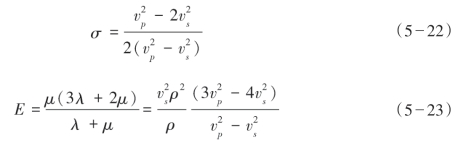
因此，为了能够直接从叠前反演中得到杨氏模量和泊松比，宗兆云等（2012）推导出了一种基于杨氏模量和泊松比的新的反射系数近似方程，并建立了一种稳定获取杨氏模量和泊松比的叠前地震直接反演方法。

由方程Aki-Richard出发，建立反射系数与纵横波模量和密度的关系式为：

式中，M为纵波模量，与介质抗压缩性和硬度直接相关，体现储层骨架和流体信息；μ为横波模量，与介质抗剪切性和刚度直接相关，体现储层骨架信息。ΔM/M、Δμ/μ分别为纵、横波模量反射系数。

在各向同性介质中，纵、横波模量与杨氏模量和泊松比的关系为：

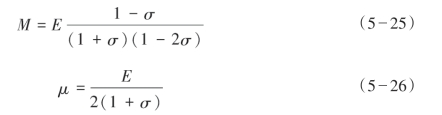
因此，在Aki-Richard近似方程式的基础上，可推导得到基于杨氏模量和泊松比的地震波反射系数为：

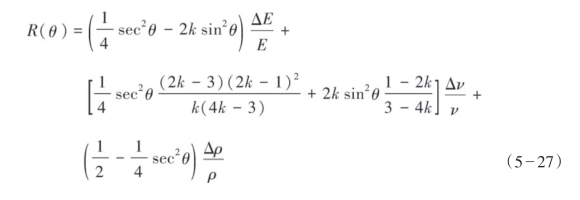
式（5—27）建立了纵波反射系数与杨氏模量反射系数、泊松比反射系数及密度反射系数的线性关系，称之为YPD近似方程。以式（5—27）为基础，可以通过叠前地震反演获得页岩地层脆性指示因子：杨氏模量和泊松比。

利用Goodway等（1997）根据实测资料给出的含气砂岩模型（如图5—27所示），对YPD方程、精确Zoeppritz方程和Aki-Richard近似方程计算的反射系数的精度进行分析。入射介质波阻抗小于透射介质波阻抗的界面称为正波阻抗界面，反之称为负波阻抗界面。上述模型中，上覆页岩、下伏含油气砂岩的反射界面就是负波阻抗界面，而上覆砂岩、下伏页岩的反射界面为正波阻抗界面。以上述模型为基础，分别用精确的Zoeppritz方程、Aki-Richard近似方程、YPD近似方程计算得到不同界面处的反射系数及近似方程与精确方程的残差。图5—28和图5—29分别为正负波阻抗界面对比分析，图5—28（a）、图5—29（a）为分别用精确的Zoeppritz方程、Aki-Richard近似方程、YPD近似方程计算得到的反射系数随入射角的变化；图5—28（b）、图5—29（b）为Aki-Richard近似方程、YPD近似方程计算得到反射系数与精确方程计算得到的反射系数的差值随入射角的变化。由图可知，基于YPD近似方程得到的反射系数在入射角为40°左右时仍与精确Zoeppritz方程有较好的近似，能够适用于较大角度入射情况下反射系数的准确求解，能够满足叠前地震反演的要求。

图5—27　含气砂岩模型（Goodway等，1997）

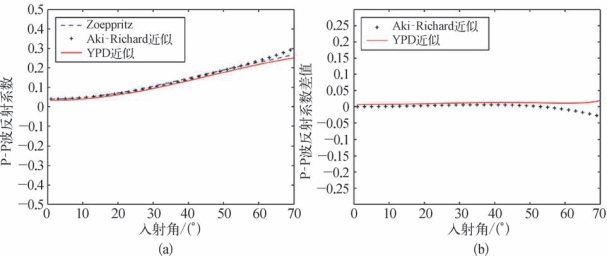
图5—28　正波阻抗界面反射系数对比（宗兆云等，2012）

（a）不同方程情况下反射系数对比；（b）不同方程情况下反射系数差值对比

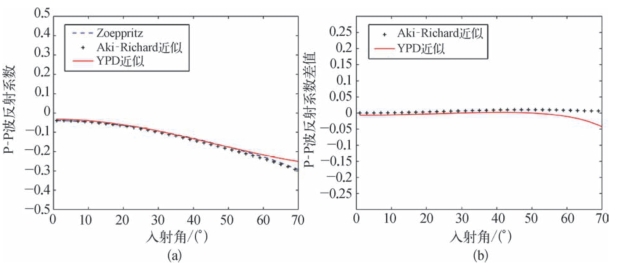
图5—29　负波阻抗界面反射系数对比（宗兆云等，2012）

（a）不同方程情况下反射系数对比；（b）不同方程情况下反射系数差值对比

为验证YPD—AVA叠前地震反演的可行性和稳定性，可采用实际单井模型进行验证。模型测试中采用主频为40 Hz的雷克子波。图5—30中蓝色曲线为某工区通过实际测井资料计算并通过时—深转换得到的时间域杨氏模量、泊松比和密度曲线，采用精确Zeoppritz方程进行正演得到角度域叠前角度道集，然后利用YPD—AVA叠前地震反演方法实现杨氏模量、泊松比和密度参数反演。图5—30（a）和图5—30（b）分别为无噪声情况下角度域合成地震记录及杨氏模量、泊松比和密度参数反演结果，其中红色曲线为反演结果，反演结果表明，在无噪声情况下，该方法能够获取与真实值基本吻合的杨氏模量、泊松比和密度，验证了方法的可行性。为进一步验证方法的稳定性，在合成记录中加入了随机噪声以符合实际地震资料的情况，图5—31为信噪比为5∶1情况下的角度域合成地震记录与反演结果，可以看出，在加入噪声的情况下，该方法能够获取与真实值有较高吻合度的杨氏模量、泊松比，但密度反演的结果在局部有些不合理。这主要是因为密度对反射系数值的影响较小，在使用AVO近似公式进行反演时，除了要保证有大角度的数据，而且要保证地震数据的信噪比要高，否则很难在含有噪声的情况下获得合理的密度参数。(www.xing528.com)

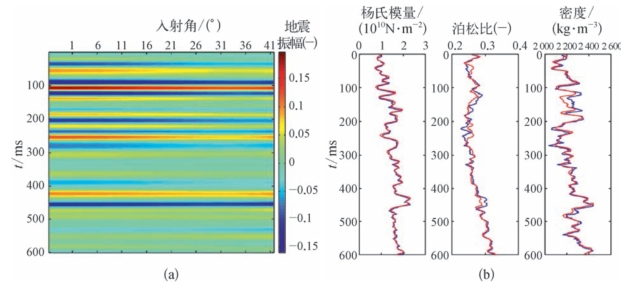
图5—30　（a）无噪声情况下角度域合成地震记录；（b）无噪声情况下反演的杨氏模量、泊松比和密度结果（红色曲线为反演结果，蓝色为实际模型）（宗　兆云等，2012）

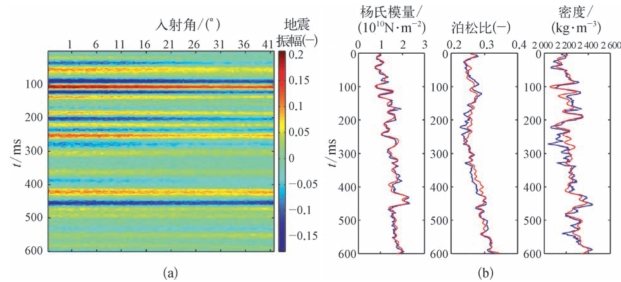
图5—31　（a）信噪比为5∶1角度域合成地震记录；（b）反演的杨氏模量、泊松比和密度结果（红色曲线为反演结果，蓝色为实际模型）（宗兆云等，2012）

Connolly（1999）首先提出弹性阻抗（EI）的概念，并有学者认为EI在抗噪能力方面比叠前AVO反演有优势（Guillaume，2000）。Connolly的弹性阻抗方程是纵、横波速度和密度的函数，从Connolly方程的弹性阻抗反演数据体中可直接提取纵、横波速度和密度数据体，如果由提取出的纵、横波速度和密度间接计算脆性指数数据体，这样就引入了人为误差，从而使得到的脆性指数误差较大。为得到更准确的脆性指数数据体，减小计算误差的累积效应，我们希望通过某种方法直接提取脆性指数数据体。

在此，用脆性弹性阻抗表示反射系数，即：

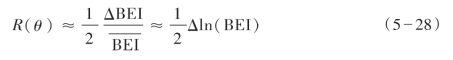
式中，BEI表示脆性弹性阻抗。将上式代入YPD反射系数近似公式，得到：

令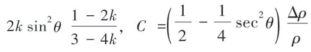，式（5—29）经过变形得到：

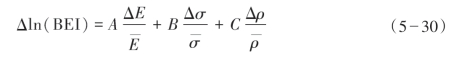
将相对变化用对数形式表示，式（5—30）可表示成：

两边取积分并将其指数化，以此消掉等式两边的微分项和对数项得到：

脆性弹性阻抗公式存在求取的数值量纲随角度变化很大的问题。这样不方便进行不同角度的BEI数值比较，并且在实现反演的过程中需要先转换量纲，给实际工作带来不必要的繁琐。为此，需对脆性弹性阻抗公式进行标准化处理，消除量纲尺度随入射角变化的问题。通过引入四个参考常数，即BEI0、E0、σ0和ρ0，可以得到标准化形式：

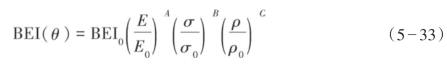
式中，E0、σ0和ρ0分别定义为E、σ和ρ的平均值，通过BEI0的标定，可以使函数变得更加稳定，并且流体弹性阻抗量纲与声阻抗一样。

脆性弹性阻抗体的反演是井震标定、子波提取、建立低频模型多个步骤的综合，总结为以下几步：首先根据实际地震数据划分不同的角度范围，叠加得到不同角度数据体；根据划分的不同角度计算井中不同的伪测井曲线；接下来利用不同的地震角叠加数据体和相应角度的FEI井曲线分别提取不同角度子波，并进行层位标定；最后利用约束稀疏脉冲反演对不同角道集数据体进行反演。约束稀疏脉冲弹性阻抗反演处理流程如图5—32所示（分为三个角道集的情况）。

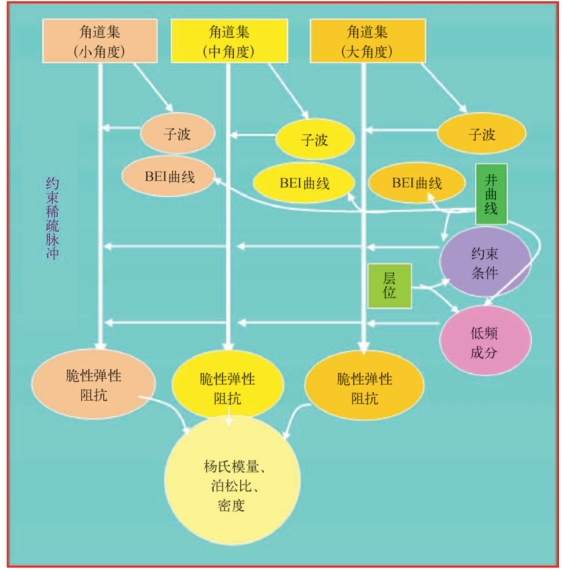
图5—32　基于YPD近似方程的脆性阻抗反演流程