页岩气地震勘探技术：叠前AVO弹性参数反演

叠前地震反演的理论基础是描述平面波在水平分界面上反射和透射的Zoeppritz方程。尽管该方程早在20世纪初就已经建立，但由于其数学上的复杂性和物理上的非直观性，一直没有得到直接的应用。为了克服由Zoeppritz方程导出的反射系数形式复杂及不易进行数值计算的困难，许多学者对Zoeppritz方程进行了简化。Koefoed（1955）将原来7个独立变量简化为5个独立变量；Bortfeld（1961）详细论述了垂直入射的平面纵波反射系数近似计算方法，并给出了区分流体和固体的简化方程；Aki和Richard（1980）在假设相邻地层介质弹性参数变化较小的情况下对Zoeppritz方程进行了近似，给出了较为简单直观且精度较好的反射和透射系数的近似表达式。在此基础上，许多学者对Aki-Richard方程重新推导、归纳，分别以不同形式的参数变量表示PP波反射系数。其中，Shuey（1985）给出了突出泊松比的相对反射系数近似表达形式；Smith和Gidlow（1987）提出了在假设介质速度和密度满足经验公式条件下的加权叠加分析方法，并给出了近似式；Gidlow（1992）给出了以相对波阻抗变化表示的近似方法；Mallick（1993）给出了用射线参数表示的反射系数近似形式；Fatti（1994）等给出了以相对波阻抗变化表示的近似方法；Goodway（1997）利用拉梅常数对反射系数进行了近似；Xu和Bancroft（1997）给出了直接利用拉梅常数和剪切模量表示的反射系数近似方法；Gray（1999）利用体积模量、拉梅常数、剪切模量的相对变化量对Richards近似进行了变换，给出了一种与之不同的表达形式；Yanghua Wang（1999）利用岩性分界面两侧的速度、密度及慢度等关系给出了一种反射系数相对于炮检距的非线性近似。

在弹性阻抗反演方面，Yin等（2004）提出利用Connolly弹性阻抗方程从三个角度反演的结果中通过计算提取纵、横波速度和密度参数的方法，继而可以得到纵、横波阻抗，拉梅常数，泊松比等丰富多样的岩性参数，从而进行地下储层的展布情况及含油气性预测。李爱山等（2007）介绍了叠前AVA多参数同步反演技术，利用三个不同角度的叠加数据体同步反演出纵、横波阻抗和密度参数。为了得到更准确的岩石物性参数，减小计算的累计误差，人们希望从反演结果中直接提取岩石物性参数。王保丽等（2007）提出了基于Gray近似的弹性波阻抗反演方法，通过对Gray近似方程进行积分推导出新的弹性阻抗方程，表示为拉梅常数、密度和入射角的函数，通过反演和参数提取可以直接得到拉梅常数，减小了计算的累计误差。

叠前地震反演技术是油气勘探领域正在兴起的一项新技术，通过研究地下介质的地震反射波振幅随炮检距的变化来反映地下介质的岩性和孔隙流体的性质，进而直接预测储层。AVO叠前反演所依据的是岩石物理学理论和振幅随偏移距变化理论，通过借助Zoeppritz方程或近似式，最终导出泊松比σ、拉梅常数λ、体积模量K、剪切模量μ和杨氏模量E等弹性参数，进而进行岩性识别。

下面简单回顾一下不同的Zoeppritz方程近似公式。

（1）Aki-Richard近似方程

Richard和Frasier研究了性质相近的反射场半空间之间的反射和透射问题，给出了以速度和密度相对变化表示的反射系数近似方程。1980年，Aki和Richard对Richard和Frasier等近似进行了综合整理，给出了类似的近似方程。假设相邻两层介质的弹性参数变化较小，因此和其他值相比为小值，假定所有角度θ1、θ2、θ3、θ4均为实数，而且入射角不超过临界角，根据斯奈尔定理，能够得到速度跃变的一级近似线性化近似方程。

式中，表示随角度变化的PP波反射系数，和θ—分别表示平均P波速度、平均S波速度、平均密度比值及分界面的入射角和透射角的平均角度。类似的，Δα、Δβ、Δρ是界面两侧P波速度，S波速度及密度的变化量。

（2）Shuey近似方程

1985年，Shuey对前人各种近似进行重新推导，进一步研究了泊松比对反射系数的影响，提出了反射系数的AVO截距和梯度的概念，证明了相对反射系数随入射角（或炮检距）的变化梯度主要由泊松比的变化来决定，给出了用不同角度项表示的反射系数近似方程，为AVO解释提供了理论基础。

其中

式中，为反射界面两侧介质的平均泊松比，即；Δσ为界面两侧泊松比之差，即Δσ＝σ2—σ1。

第一项参数A表示P波垂直入射（θ＝0）时的反射系数；第二项参数B称为梯度项，在入射角为中等入射时（0°<θ≤30°），它将影响振幅随炮检距的变化规律，反映了地层岩性的变化；第三项参数C在θ >30°时，影响振幅随炮检距的变化规律。在入射角小于30°时，sin2θtan2θ≤0.083，也比较小，则第三项可以忽略，此时Shuey方程可以简化为：

Shuey两参数近似方程直观地表达了PP波反射系数与介质的弹性参数及入射角之间的关系，使AVO异常识别由定性阶段进入了定量阶段，促进了AVO技术的发展。应该指出，利用该方程反演岩性参数，只需知道背景纵波速度的信息，而不需要横波信息，这样在反演过程中，消除了背景横波信息所引起的系统误差。所以，许多反演工作使用该方程反演岩性参数。但在该反演方程中，B项属性参数没有明确的物理意义，需要进行二次转换，且泊松比的变化取决于反射界面两侧的纵、横波速度的变化，这在很大程度上限制了参数估计的有效性，而且可能使得Δσ的估计带有较大误差。

（3）Smith和Gidlow近似方程(www.xing528.com)

1987年，Smith和Gidlow在Aki-Richard近似方程的基础上，利用P波速度与密度的经验关系式，给出如下近似式。

式中，g为指数。Gardner认为P波速度与密度之间存在指数关系。

近似方程式（5—17）将加权叠加技术应用于岩性参数的估计。属性参数是P波速度反射系数和S波速度反射系数。从矩阵的条件数分析得到（图5—26），Smith和Gidlow近似方程比两参数Shuey近似方程具有更好的稳定性。加权叠加的方法不受条件的限制。对于速度垂直变化的介质，可以结合测井数据，利用射线追踪来获取角度等信息。虽然，该近似方法能够较为精确地反演岩性参数，但参数估计的精确度依赖于经验关系式的精确度，这在很大程度上限制了其应用范围。特别是经验关系式与实际地层相差较多时，解可能不收敛或得不到解，同时很可能引入小角度误差。

（4）Gidlow近似方程

为了避免Smith和Gidlow近似方法过多地依赖Gardner经验方程，1992年，Gidlow等对Aki-Richard近似方程进行重新整理，给出以波阻抗反射系数表示的近似方程。

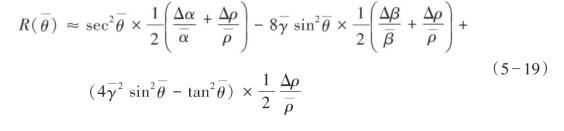
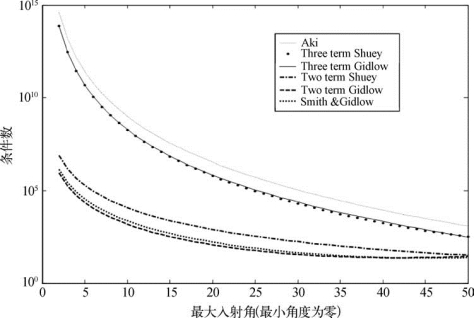
图5—26　几种近似方程的条件数分析

Gidlow近似方程式中的属性参数分别表示P波阻抗反射系数、S波阻抗反射系数及密度反射系数。在小角度情况下，密度项的系数较小，密度的变化也较小，所以，得到其两参数近似方程。

Debski和Tarantola（1995）认为以波阻抗反射系数作为参数进行AVO反演，可以使反演问题相对稳定。但采用Gidlow近似方程反演属性参数，需要背景纵、横波速度的信息，从而易产生背景横波信息所带来的误差，对此可建立平滑的背景纵波速度，利用岩石物理的经验关系及研究方法，可以有效减小误差。

（5）Gray近似方程

Goodway等（1997）在分析了拉梅常数（压缩模量λ和剪切模量μ）对碳氢化合物的敏感程度后认为，λ/μ对含油气饱和的储层非常敏感，并在声波测井参数约束的情况下，利用Goodway近似方程进行了AVO分析。该近似主要体现了拉梅常数（压缩模量λ和剪切模量μ）对碳氢化合物的敏感程度。Xu和Bancroft（1997）结合Aki-Richard及Goodway等方法利用拉梅常数（λ，μ）、体积模量k等给出了完全隐含波速的近似方程，由于密度的相对变化较小，因此用其前两项参数基本上可以反映小于45°入射角的反射特性。Gray（1999）结合前述的近似方程，在Aki-Richard近似方程式的基础上，以拉梅（压缩模量λ和剪切模量μ）反射系数及密度反射系数表示的近似方程如下。

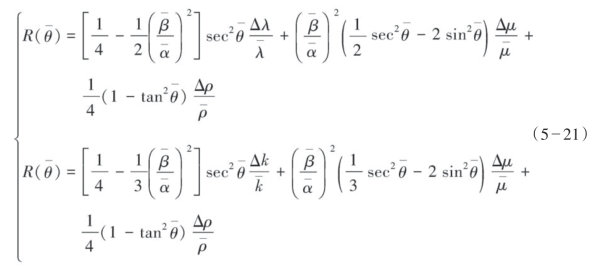
该式最大的特点是直接利用与含油气储层十分敏感的弹性参数的相对变化表示整个反射系数。Dontown（2005）指出包含密度的反射系数，如阻抗，比不包含密度的反射系数，如速度，更趋于稳定。