页岩气储层岩石物理建模：新技术预测成果

对于页岩气储层来说，地震波速度主要受矿物、孔隙度、裂缝等孔隙空间结构及有机质的影响，对于前三者，前人都有大量的讨论（Kuster和Toksöz，1974； Sun等，1991，2004； Anselmetti和Eberli，1993，1999； Baechle等，2008； Sun等，2012），而对于有机质对地震波速度的影响则很少见到。在岩石中存在的有机质，其弹性模量与矿物差距较大，接近于流体，表现为柔性，但是由于剪切模量不为零，又不同于流体。这给泥页岩的岩石物理建模造成了很大的困难。本节在对储层特征分析的基础上，讨论了工业界常用的岩石物理模型在泥页岩中的适用性，针对性地提出了包括矿物、孔隙度、孔隙类型、有机质、流体的页岩气储层岩石物理模型。

1.经典岩石物理模型

岩石可视为一种由固体骨架和流体充填的孔隙所组成的饱和多孔介质。目前已有很多种方法描述多孔介质中储层物理参数和岩石性质之间的关系，其中包括边界方法、经验公式和物理模型等。在地球物理中，这些岩石物理模型不仅在测井分析、地震反演、属性分析及储层和流体识别等各个方面都起着重要的理论基础作用，并且在油藏动态监测中也逐渐得到人们的重视。

进行速度预测的岩石物理模型需要包括三部分内容：① 岩石中的各个组成部分（矿物、孔隙、流体）；② 各个组成部分的弹性模量；③ 各个组成部分之间的几何细节。工业界常用来做速度预测的模型从简单到复杂依次有Wyllie时间平均公式（Wyllie，1956）、Gassmann理论（Gassmann，1951）、Kuster-Toksöz模型（Kuster和Toksöz，1974），以及针对砂泥岩的Xu-White模型（Xu和White，1995）。

1）Voigt-Reuss-Hill平均

最简单且最常用的等效介质模型是Voigt和Reuss模型。Voigt模型给出了N种矿物组成的复合介质的有效弹性模量MV：

式中，fi是第i种组分的体积分数；Mi是第i种组分的弹性模量。Voigt有效弹性模量是一个代数平均，它代表上边界。Reuss模型给出了有效弹性模量的下边界MR：

数学上，Voigt和Reuss公式中的M可以表示任何模量，如体积模量K、剪切模量μ、杨氏模量E等。但是，它仅用来计算剪切模量和体积模量的Voigt和Reuss平均，然后由这两个量来计算其他模量，这使得Voigt和Reuss平均更有意义。

Hill曾建议利用对它们进行平均的方法来提供岩石有效模量的更实际的评价。这个方法对于含有不同矿物成分的岩石骨架的弹性模量的评价十分有效。

2）Hashin-Shtrikman边界

各向同性弹性复合介质的最佳范围是Hashin-Shtrikman（HS）边界，它给出尽可能窄的弹性模量上下限范围，且不需要具体说明组成成分的几何形状。对于由两种成分组成的复合介质，Hashin-Shtrikman边界为：

式中，K1，K2是单相的体积模量；μ1，μ2是单相的剪切模量；f1，f2是单相的体积分数。

上下界限是通过交换相的下标1和下标2计算出来的。一般地，当刚性较大的相的下标是1时，上面的表达式给定上限；当刚性小的相的下标是1时，则给定下限。因为许多有效介质模型假设矿物模量是单相的，当把混合矿物表示成一种“平均矿物”的模量时，它等于由HS计算的混合矿物的边界之一或它们的平均。另一方面，当组分差别很大时，例如矿物和孔隙流体，那么上下限差别很大，会丢失一些预测值。

3）Gassmann方程

1951年，Gassmann提出预测岩石体积模量的Gassmann方程。它建立了岩石基质模量、孔隙度、流体和干岩石模量之间的关系，为孔隙流体与地震波速的联系架起了桥梁。据统计，有关岩石物理的文献，三分之一以上都涉及了Gassmann方程，可见其重要性。比较常用的Gassmann方程的形式如下：

式中，K是饱和孔隙流体时的岩石体积模量；φ是孔隙度；Kd是干岩石的体积模量；Ks是岩石基质的体积模量；Kf是孔隙流体的体积模量。Gassmann方程的基本假设条件是：① 岩石（基质和骨架）是各向同性、弹性、单矿物和均质的；② 孔隙空间具有很好的连通性，并保持压力均衡；③ 孔隙空间充满流体（液体、气体或混合物）；④ 岩石是一个封闭的系统，没有穿越边界的孔隙流体运动；⑤ 流体和岩石骨架之间没有化学作用（剪切模量不受流体的影响）。

Gassmann方程假设岩石相同的矿物模量和孔隙空间是统计性各向同性的，但不考虑孔隙形状的变化。更重要的是，式（4—23）适用于低频情况，当频率足够低，使得孔隙流体有足够的时间流动并没有波动诱发产生孔隙压力梯度时才成立，这也就说明了该公式非常适用于地震资料频带（<100 Hz）。

Gassmann方程中干岩样的体积模量一般是未知的，需要通过实验室测量得到，也有很多人提出了一些简单的计算公式，如Biot（1956）提出了Kd与Kma之间的关系：

式中，B也被称为Biot系数。对于B的取值，一般看成是孔隙度的函数近似求得，采取Nur等（1991）提出的公式：

式中，φ是孔隙度，φcrti是临界孔隙度，灰岩一般取60%。

4）Brown-Korringa固体替代理论

Brown-Korringa（1975）方程是利用岩体弹性张量表示流体替代的理论，也称为各向异性的流体替代。经过简单的改造则可以用来进行固体替代计算含干酪根岩石的体积模量和剪切模量，即

式中，φ是可以转换成TOC的干酪根占有的体积分数；分别为基质、干岩石、饱和岩石的四阶张量；sφ，sTOC分别表示孔隙空间及孔隙空间填充的TOC的柔度张量。

5）Kuster-Toksöz模型

Kuster和Toksöz利用散射理论建立了一个应用很广泛的两相介质的模型，把孔隙度和孔隙纵横比与岩石的体积和剪切模量联系起来。根据这一模型，多孔岩石用整体各向同性固体骨架以及随机分布的孔隙和孔隙流体来表征，并假设孔隙形状为椭圆形，通过孔隙的纵横比来描述孔隙形状的变化。孔隙纵横比定义为椭圆短轴与长轴之比，一般在0～1之间，越接近于0表示孔隙越扁，越接近于1表示孔隙越圆，从而建立了孔隙度和孔隙纵横比与纵横波波速的联系。Kuster-Toksöz模型假设：① 等效介质由具有不同性质的两相组成；② 单相（骨架）是连续的统一体而另一相是随机嵌入的内含物；③ 内含物（孔隙）非常稀疏，它们彼此间无相互联系、不重叠；④ 波长远大于内含物的尺寸。Kuster-Toksöz（KT）方程的表达式如下：

式中，K′为孔隙内含物的体积模量；μ′为孔隙内含物的剪切模量；K为有效体积模量；μ为有效剪切模量；Km和μm分别为骨架体积模量和剪切模量；αl为孔隙纵横比。式（4—28）需要φ/α<<1。泥页岩孔隙纵横比的典型值是0.035，砂岩为0.12，因此该方程仅适用于小孔隙。KT方程中Tiijj（αl）和F（αl）的计算公式为：

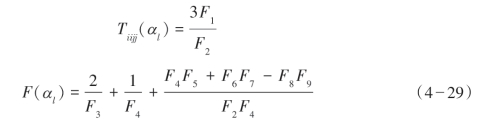
其中

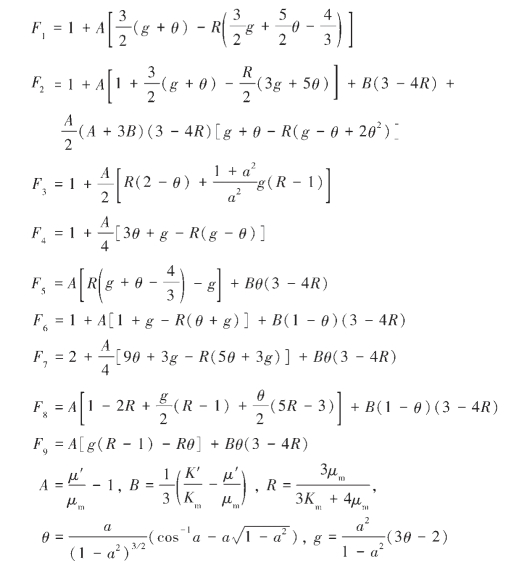
Kuster-Toksöz模型计算等效体积模量时，如果所有孔隙为球形（纵横比为1），则变为Gassmann方程，有效剪切模量不受饱和流体影响。但是，纵横比较小的孔隙求得的干岩石的有效剪切模量远小于饱含水情况下的模量。Kuster-Toksöz方法经常用来计算干岩石模量。它的局限性在于孔隙纵横比必须已知而且它仅适用于各向同性岩石。

Berryman（1995）根据Kuster-Toksöz理论定义了球形、针形、盘形和硬币状裂缝四种三维孔隙形状下岩石的有效体积模量Kkt、μkt，定义式如下：

式中，Pmi、Qmi的值对于不同的孔隙类型是不同的。

Kuster-Toksöz模型假设背景相（骨架）是各向同性的，而另一相（孔隙或孔隙流体）随机嵌入其中，即各个孔隙之间是孤立的、不连通的，孔隙尺寸远远小于波长；同时，要求孔隙具有稀疏性，即满足：

式中φ为孔隙度，α为孔隙纵横比，说明Kuster-Toksöz模型只适用于孔隙度较低的岩石。

另外，KT模型是一个高频模型，适用于实验室超声条件下，所以通常用该模型来计算不含流体的干岩石的体积模量，再用Gassmann方程理论来往空腔中加入流体。

6）微分等效介质（DEM）理论

微分等效介质（DEM）岩石物理模型通过往固体相中逐渐加入填入物来模拟双相混合物（Norris，1985；Zimmerman，1991），固体相是相1，之后逐步加入相2的材料。此过程一直进行到需要的各成分含量达到为止。DEM理论并不是对称地对待每个组成成分，被当成固体矿物或主相的成分可以有不同的选择，且最终的等效模量会依赖于达到最终混合物所采用的路径。用相1作为主相并逐渐加入材料2，与以相2作为主相并逐渐加入材料1，会导致不同的等效属性。公式可以表示为：

式中，分别代表所求的干岩石的体积模量和剪切模量；Ki，μi分别代表填入物的体积模量和剪切模量；y代表相2所占的百分比；P，Q为孔隙因子。

7）自适应（SCA）理论

Hill（1952）与Budiansky（1965）提出了自洽模型（Self-consistent Approximation，SCA），其基本建模思想为：将要求解的多相介质放置于无限大的背景介质中，且背景介质的弹性参数任意可调。通过调整背景介质的弹性参数，使背景介质的弹性参数与多相介质的弹性参数相匹配，当有一平面波入射时，多相介质不再引起散射，此时背景介质的弹性模量与多相介质的有效弹性模量相等。该方法既考虑到孔隙形状的影响，又能够适用于孔隙度较大的岩石。这种方法仍然是计算的内含物的变形，但是该方法中不再选用多相材料中的一相作为背景介质，而是用要求解的有效介质作为背景介质，通过不断改变基质来考虑内含物之间的相互作用。因为该方法考虑了内含物的相互作用，所以能适用于孔隙度较大的岩石。

式中，i代表第i种材料，xi为第i种材料的含量；P、Q为表征孔隙相弹性性质的系数。

8）Xu-White岩石物理模型

Wyllie方程将岩石中的各个组成部分等效为层状，不考虑几何细节，是最简单的岩石物理模型；Gassmann方程将岩石等效为颗粒与球体状的孔隙组成，不考虑孔隙形状的变化；Kuster-Toksöz模型在假设孔隙形状为椭球体的前提下通过引入可以任意调整的二维孔隙表面比将各种尺寸的孔隙考虑到模型计算中，理论上可以考虑孔隙形状的变化，但是它作为高频的模型要求岩石内的孔隙是稀疏且孤立的，这就限制了孔隙和孔隙内流体之间的相互作用。

Xu-White模型是在上述三种岩石物理模型的基础之上，再加上微分等效介质理论（DEM）得到的合成模型，是目前应用最为广泛的岩石物理模型，它将岩石孔隙划分为大孔隙表面比（约0.12）的砂岩孔隙和小孔隙表面比（约0.02～0.05）的泥岩孔隙，同时利用微分介质理论将每种孔隙再划分为多达上百个小孔隙以满足Kuster-Toksöz模型中对孔隙稀疏性的要求，同时，使用Gassmann方程往干岩石中加入流体，计算饱和流体岩石的弹性模量，使其兼具Kuster-Toksöz模型和Gassmann方程考虑孔隙流体影响的优点。但是这个模型也有缺点：首先，它使用固定的二维孔隙表面比，不能够很好地描述复杂的孔隙类型，对于裂缝，尤其是表面比很小（甚至趋于零）的裂缝，该模型不能很好地描述；其次，它将岩石中的泥岩孔隙、砂岩孔隙的表面比固定，限制了其描述速度的范围。通过将这四种岩石物理模型应用于泥页岩储层中（如图4—2所示），可以发现，在非目的层段，四种岩石物理模型得到的速度预测结果基本都能与实测结果相吻合，但是在目的层段差距都比较大，其中Xu-White模型得到的结果相对其他较好。

(www.xing528.com)

图4—2　常用岩石物理模型在泥页岩速度预测中的应用效果

（黑色曲线为实测纵波时差（AC）与横波时差（Dts），彩色曲线为预测结果，其中下画线后的文字代表方法，分别为Xu-White（XW），Kuster-Toksöz（KT），Gassmann方程，以及Wyllie方程；右侧为箭头所指示深度段的典型岩心图，其中a.深灰色含灰泥岩为主，夹灰色粉砂质泥岩、灰色介壳灰岩、深灰色页岩；b.灰黑色含介壳页岩为主，夹薄层介壳灰岩；c.灰黑色含介壳页岩，夹薄层介壳灰岩，网状方解石脉及孔洞发育；d.灰色含泥细砂岩）

通过与岩心的对比发现，在常规的岩石中，比如含泥细砂岩中，各种常规的岩石物理模型都可以得到较好的效果，其中Xu-White模型的效果最好，纵横波速度都能与实测的相吻合。但是在含气层、页岩层段，这些岩石物理模型预测效果都较差，而这些层段的岩心有比较明显的特征，具体为：① 含有比较复杂的孔隙系统，比如生物孔隙、网状的裂缝系统等；② 页岩及泥岩中富含一定的有机质；③ 赋存天然气。这些因素综合起来使得在目的层的泥页岩储层中，常规岩石物理模型不适用。因此，需要发展能够描述复杂孔隙、有机质及能够更加精确地描述含气裂缝的岩石物理模型。

2.页岩气储层岩石物理模型

1）DEM-Gassmann岩石物理模型

DEM-Gassmann模型是基于Berryman（1992）微分等效介质理论（简称DEM）、Gassmann（1951）方程及Wu（1966）的任意孔隙表面比、Berryman（1995）三维特殊孔隙的划分上构建了该岩石物理模型。其建模思想及流程为：① 使用Voigt-Reuss-Hill模型求取混合固体矿物的弹性模量；② 使用DEM理论，计算干岩石的弹性模量；③ 使用Gassmann方程往孔隙中加入流体，计算饱和流体岩石的弹性模量；④ 利用纵横波速度与弹性模量、密度之间的关系式求得最终的饱和流体岩石的纵波速度P和横波速度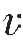S。DEM中的P、Q为表征孔隙相弹性性质的系数，其取值方式有两种，一是Wu（1966）的任意孔隙表面比方式，二是Berryman（1995）的四种特殊三维孔隙的方式。两种取值方式分别对应的计算步骤如下。

（1）Wu（1966）的任意孔隙表面比取值方式

设定孔隙表面比a的初值，当结果与实测结果不匹配时需要不断地调整a的值。孔隙表面比a是速度预测的重要参数，一般a在0～1，越接近于0表示孔隙越扁（裂缝），而接近于1则表示为圆形孔（孔洞）。

（2）Berryman（1995）的三维特殊孔隙取值方式

Berryman（1995）提出将实际岩石孔隙等效模拟成球形孔隙、针形孔隙、碟形孔隙、裂缝型孔隙，如表4—2所示，研究岩石物理模型只选取四种特殊三维孔隙形状中的三种，即球形（表征溶蚀洞）、针形（表征溶蚀孔）、碟形或便士状裂缝（表征缝）。主导孔隙所占相应岩性总孔隙的比例系数为CD（一般在0.6～1.0取值），第一个次要孔隙占相应岩性总孔隙的比例系数为CS，则后面两种孔隙所占的比例依次是0.1CS、0.01CS。再将这种多种孔隙类型进行微分化加入岩石中，可以通过调整比例系数及泥质中裂缝纵横比而达到与实测结果较好地吻合。同时主导三维孔隙的假设符合实际的砂质、灰质和泥质孔隙空间的抽象形态，因此能够保证在调整参数时不会背离实际的地质情况。

表4—2　四种三维孔隙的几何尺寸常量P、Q及其在砂岩与泥岩孔隙中的比例系数

其中，

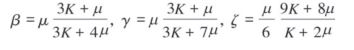
利用最优化测井解释了黏土、石英、方解石和干酪根，在此基础上研究干酪根的添加方式对岩石物理建模和速度预测的影响，分两种情况，即干酪根作为基质与干酪根作为类孔隙物进入岩石。如图4—3所示，AC_c_tff表示干酪根作为基质矿物添加进入岩石所得到的速度预测结果；AC_c_K、AC_c_P表示干酪根作为类孔隙颗粒加入岩石，其中AC_c_K是首先在干岩石中按照DEM-Berryman理论依次加入干酪根、孔隙，随后利用Gassmann方程加入流体，使其成为饱和岩石，而AC_c_P是首先在干岩石中按照DEM-Berryman理论依次加入孔隙、干酪根，随后利用Gassmann方程加入流体，使其成为饱和岩石。

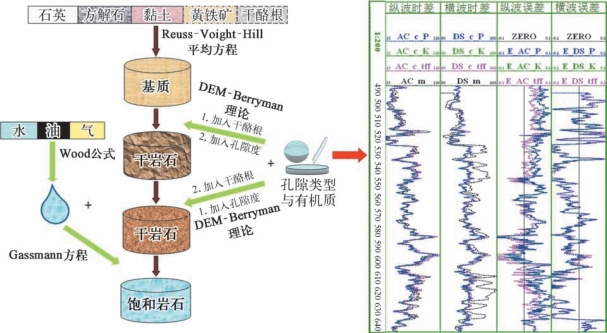
图4—3　干酪根的添加方式对速度预测结果产生的影响

通过AC_c_K、AC_c_P、AC_c_tff曲线对比可以看出，添加干酪根的方式对速度预测结果会产生一定的影响，而干酪根添加的先后顺序对速度预测的结果基本没有影响。其中，在非储层段，把干酪根作为基质矿物添加进去时速度预测效果相对较好，而在储层段干酪根作为类孔隙颗粒加入时效果好。

上述研究发现：从理论上来讲，泥页岩矿物组分解释的精细程度越高，其所建立的岩石物理模型可信度越高，从而使速度预测的结果越接近实际结果。在非储层段，该结论得到验证，但是在储层段，使用精细矿物分析的结果反而不如使用非精细岩性分析法得到的结果，这是由页岩气储层段的复杂性、测井解释中的微小误差、岩石物理建模过程中参数的选择共同决定的，对于使用多矿物分析结果进行速度预测，还需要进一步深入研究。有机质既不同于基质，又不同于流体，在岩石物理建模过程中，采用何种方式加入，对于页岩气储层的岩石物理建模非常重要。通过不同的加入方式及顺序的测试，认为将有机质作为类孔隙颗粒，以微分（DEM）方式加入干岩石中，可以得到更好的效果。对于关于有机质的岩石物理模型，还需要进一步的研究。

2）改进的Xu-White岩石物理模型

针对Xu-White模型的缺点以及页岩气储层的特征，将岩石等效为矿物、含流体孔隙及干酪根颗粒组成，其中矿物包括黏土、石英、方解石。孔隙可分为两种：① 砂质与灰质孔隙；② 泥质孔隙。在砂质中，孔隙多为砂质颗粒间的粒间孔，使用以球体等刚性孔隙类型为主的、以硬币状裂缝等柔性孔隙为次的孔隙谱来描述；在灰质中，孔隙多表现为孔洞状及生物孔，因此使用与砂质孔一样的孔隙谱进行描述。而泥质中的孔隙多为裂缝及微裂缝，因此，使用以裂缝状的柔性孔隙为主，以球体等刚性孔隙为次的孔隙谱来描述。对于干酪根，由于其在岩石中属于柔性成分，既不同于矿物，又不同于流体，因此使用硬币状及裂缝状的柔性颗粒来描述，由于孔隙及有机质的赋存方式为稀疏性存在，因此将干酪根及孔隙以微分方式逐渐加入，每次加入后，新的岩石都作为背景，直到加入的量达到要求。图4—4为具体等效方法的示意图。

图4—4　宏观与微观储层特征及等效方法

（岩心特征：a.灰黑色含介壳页岩为主，夹薄层介壳灰岩；b.灰黑色含介壳页岩，夹薄层介壳灰岩，网状方解石脉及孔洞发育；c.泥岩中裂缝发育；d.海绵）

图4—5为含有机质模型页岩气储层岩石物理模型建模流程图。

图4—5　含有机质多孔岩石物理模型建模流程

核心思想及计算流程表述如下。

（1）类似于Xu-White模型将砂岩和泥岩孔隙分开考虑的办法，将岩石孔隙φtotal划分为砂质和灰质孔隙φquartz+calcite及泥质孔隙φclay，并假设两种孔隙所占的比例正比于两种岩石成分的含量，即：

式中，Vshale、Vquartz+calcite分别代表岩石中泥质、砂质与灰质所占的体积分数。

将岩石固体部分与孔隙分开考虑，则对于纯固体部分，泥质所占的体积分数可由下式得到：

（2）使用Voigt-Reuss-Hill模型求取混合固体矿物的弹性模量。

（3）使用DEM理论，计算干岩石的弹性模量。

不同于Xu-White模型将泥质和砂质孔隙分别设定二维孔隙表面比的做法，在该改进模型中，根据对砂岩和泥岩孔隙形状的主次性统计特征（Cheng和Toksöz，1979），并将灰质孔隙等同于砂质规律考虑，分别将砂质与灰质、泥质孔隙进一步划分为有一种孔隙占主导的四种三维孔隙。具体的做法是：假设砂岩与灰质孔隙的主导孔隙是球形，次要孔隙依次是针形、碟形和裂缝形；假设泥质的主导孔隙是无限裂缝形（表面比可无限小），次要孔隙依次是碟形、针形和球形。

（4）使用DEM理论，将有机质颗粒作为柔性颗粒方式加入岩石中，计算含有机质颗粒的岩石的弹性模量。

（5）使用Wood公式计算流体的弹性模量。

（6）使用Gassmann方程往孔隙中加入流体，计算饱和流体岩石的弹性模量。

（7）利用纵横波速度与弹性模量、密度之间的关系式求得最终的饱和流体岩石的纵波速度P和横波速度S。

将修正的岩石物理模型应用到页岩气速度预测中，如图4—6所示，整体来说，改进岩石物理模型的速度预测结果要好于Xu-White模型，尤其在储层段，新模型的纵波、横波预测结果与实测结果相比较都要更加吻合。

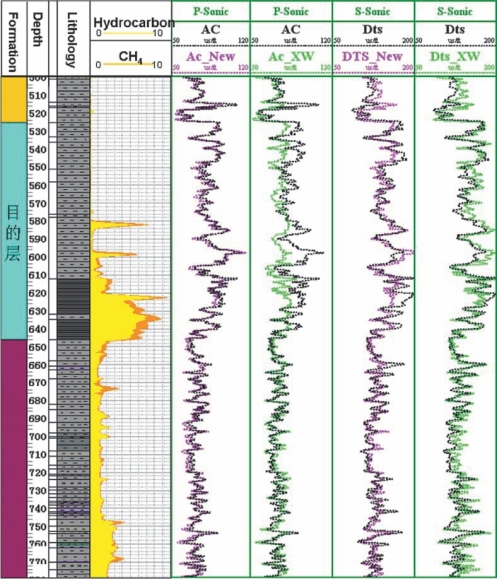
图4—6　使用改进的岩石物理进行速度预测与Xu-White模型结果的对比

3）三维SCA—DEM岩石物理模型

SCA模型虽然既考虑到孔隙形状的影响，又能够适用于孔隙度较大的岩石，但是临界孔隙度的存在使得SCA模型的应用受到一定的限制，因为对于固体相和流体相（孔隙相）组成的混合岩石，当流体相的体积分数大于60%时，SCA模型计算的剪切模量趋向于0（Berryman，1980），这意味着当流体相的体积分数大于60%时，固体相失去了连续性。由于在SCA模型中，岩石中的各相是对等的，也就是说双相介质中流体饱和孔隙度在40%～60%时，能保证双相介质中的两相都是互相连通的。所以在使用SCA模型计算岩石有效弹性模量时要注意。Agnibaha Das（2009）认为由于SCA理论中的假设是在无限大背景条件下，因此固体相和流体相具有对称性，那么反过来当固体相的体积分数达到60%左右时，由SCA模型计算得到的剪模量也为0，即流体相的体积分数必须落在40%～60%时，固体相和流体相组成的有效介质是双连通的，即SCA模型适用的有效孔隙度范围在40%～60%之间，这与绝大部分储层的孔隙度范围是不相适应的。为了解决SCA模型受限的问题，通常的做法是将SCA模型与微分等效介质模型相结合（Hornby，1994； Agnibaha Das，2009），这有效地解决了SCA模型存在临界孔隙度的限制问题。

在SCA模型和微分等效介质模型的基础上，引入Berryman三维孔隙形态，模拟不同孔隙形状对于SCA模型临界孔隙度与岩石速度的影响。在泥页岩中有机质固体充填的思想基础上，利用Brown-Korringa方程将有机质作为固体充填物，建立了富有机质泥页岩三维SCA—DEM模型。基于研究区HF—1井，利用测井解释、分析得到的矿物组分分布及孔隙度分布特征，结合建立新的岩石物理模型，其主要流程如下所述（如图4—7所示）。

图4—7　富有机质泥页岩3DSCA—DEM模型建模流程

（1）给定临界孔隙度，利用SCA理论计算临界孔隙度时的干岩石的体积模量和剪切模量；

（2）利用DEM理论逐步调整孔隙度至真实孔隙度时的干岩石的体积模量和剪切模量；

（3）利用Gassmann方程计算饱和流体岩石的体积模量和剪切模量；

（4）利用Brown-Korringa方程进行固体替代计算含干酪根岩石的体积模量和剪切模量；

（5）最后再利用纵横波速度与弹性模量、密度之间的关系式求得最终的饱和流体岩石的纵波速度P和横波速度S。

图4—8是采用3D SCA—DEM模型对某页岩气井进行纵横波速度预测并与实测纵横波速度及常规岩石物理模型预测的结果（粉红色为3D SCA—DEM模型预测结果，绿色为Xu-White模型预测结果，蓝色为KT模型预测结果）进行对比，讨论该模型在实际页岩气储层中的预测效果。从图中可以看出，预测的纵横波时差3D SCA—DEM与实测的纵横波时差AC、Dts达到了很好的吻合，相对于Xu-White模型及KT模型，此模型预测效果更佳，这就保证了3D SCA—DEM模型的适用性及可靠性。因此，这样建立在精细测井分析和岩石物理模型预测技术上得到的纵横波速度数据就为在无横波测井区同样实现叠前反演、时移地震等需要纵、横波信息联合的储层预测或监测手段带来了可能性。

图4—8　基于3DSCA—DEM模型的纵横波速度预测结果与实测纵横波及常规岩石物理模型预测结果的对比

（以HF—1井为例，左侧为实际测井曲线，右侧为岩性解释剖面，黑色曲线为实测纵横波曲线，粉红色为3D SCA—DEM模型预测结果，绿色为Xu-White模型预测结果，蓝色为KT模型预测结果）

速度预测的结果与常规的岩石物理模型（KT模型、Xu-White模型）对比表明，三维SCA—DEM模型预测结果与实测纵横波时差吻合得很好，相对于常规岩石物理模型效果更佳。