页岩气地震勘探技术：岩石物理基本概念

1.岩石物理的基本概念及其作用

岩石物理学研究岩石的物理性质（包括储层参数和物理性质）及其相互关系。由于反射地震在石油勘探中的重要作用，近年来岩石物理的研究偏重于岩石的地震弹性特性，主要反映在地震波速度等弹性参数与岩石其他性质及岩石所处状态条件的关系，研究在油藏条件下和采油过程中流体与岩石的特征改变量及其对地震特性的影响，是连接地震与油藏工程的纽带，也是把地震特征转换为油藏特征的物理基础。简言之，岩石物理分析的目的就是建立地震特性与储层特性之间的关系。

岩石物理性质的研究成果为从地震数据中提取地下岩石及其饱和流体的性质奠定了物理基础（地震反演过程）。另一方面，了解地震波特性与岩石、流体性质的关系可以帮助我们模拟地震波在复杂地表下的传播（地震正演），理解地球物理响应特征。图4—1为岩石物理作用的示意图。岩石物理在储层特性与地震特性之间的桥梁作用主要体现如下。

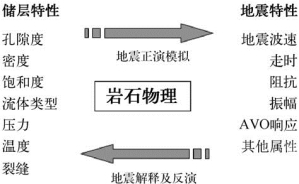
图4-1 岩石物理架起储层特性与地震特性之间的桥梁

1）地震反演

地震属性参数及反射率受控于储层矿物、岩性、流体类型、孔隙度、孔隙形状、渗透率、饱和度、韧性和裂隙、压力、温度等导致的弹性与力学参数。而地震资料直接得到的地震属性参数为时间、振幅、波形、频率、入射角、方位角等，需要将这些属性进行地震反演得到弹性与力学参数，再通过岩石物理桥梁得到储层参数。地震反演有各种各样的算法和实现策略，这里不再一一罗列。

2）地震正演

基于以矿物、岩性、流体类型、孔隙度、孔隙形状、渗透率、饱和度、韧性和裂隙等为参数的储层地质模型，通过岩石物理建模与分析，能够得到储层弹性参数，进行储层地球物理参数建模，从而可以进行地震波场正演模拟，得到以时间、振幅、波形、频率、入射角、方位角为参数的地震合成记录，岩石物理依然是桥梁和纽带。

2.岩石物理理论基础

表示岩石地震弹性物理特征的参数主要有：弹性模量、密度、纵波速度、横波速度、衰减等，它们是地震定量解释储集层的重要地震参数（通过反演得到），基本概念介绍如下。

1）弹性模量

弹性模量是反映岩石在外力作用下发生伸缩剪切和体积变化的特征参数，是联系应力应变关系的常量。正应变模量λ是正应力与正应变的比例系数（可以反映流体的变化）；剪切模量μ表示切应力与切应变之比，是阻止剪切应变的一个度量，流体无剪切模量（反映岩性的变化）；体积模量K反映在外力作用下岩石体积发生的变化，反映岩石的可压缩性；杨氏模量E是物质对受力作用的阻力的度量，固体介质对拉伸力的阻力越大，弹性越好，E越大；泊松比σ是反映岩性和含气性的重要参数，用岩石纵向拉伸和横向压缩的比值来表示，与纵、横波速度存在如下关系：

式中，纵、横波速度比γ＝P/S。实验表明，不同岩石的泊松比分布范围是不同的，它对于区分水饱和和气饱和岩石有特殊意义。综合泊松比和纵、横波速度波可以较好地区分砂岩和泥岩。

上述弹性参数存在一定关系，已知任意两个可求得其余三个，具体关系如下：

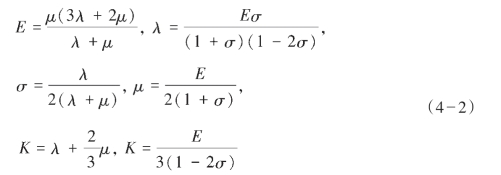
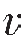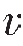2）纵、横波速度P、S

根据弹性波动方程理论，在均匀各向同性完全弹性介质中，密度ρ反映单位体积岩石的质量，纵波速度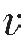P和横波速度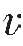S可用密度ρ、体积模量K与正应变模量λ和剪切模量μ表示如下：

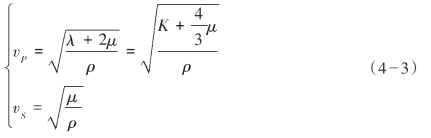
实际应用中，理论计算纵、横波速度需要知道K、μ、ρ三个参数，岩石物理建模就是建立一种计算这三种参数的岩石骨架和孔隙流体的模型。

3）岩石骨架模型

岩石模量求取之前，首先要判断岩石的骨架模型。因为，不同的骨架模型，求取的岩石模量具有一定的差异。常用到的骨架模型主要有Voigt和Reuss模型、Hashin-Shtrikman（HS）边界模型、Kuster-Toksöz模型以及Gassmann方程模型，后面详细阐述。

4）岩石模量的求取方法

干岩石的体积模量是包含流体岩石物理模型的Gassmann方程中采用的重要参数，而Gassmann方程对理解孔隙流体对地震波的效应具有重要价值，因此正确估计干岩石体积模量，对岩石物理的理论研究及一些模型的实际应用十分重要。

（1）直接测定法

直接在实验室测定干岩石的特性是获得干岩石弹性模量最常用的方法，也是最为可靠的方法。当利用超声波法（或低频测量法）测定干岩石弹性模量时，直接测量结果为纵、横波速度，干岩石的体积模量Kd和剪切模量μd可由下述公式换算得到，即：

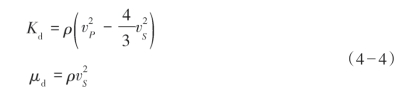
式中，ρ为干岩石的密度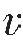；P、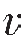S分别为干岩石的纵波速度和横波速度。直接测量需要专门的岩石物理实验室，且需要岩心样品。当不具备实验条件或所研究工区内无岩心样品时，必须考虑其他方法。下面总结了几种具有相当应用价值的干岩石体积模量Kd的计算方法。

（2）Gassmann方程法

① 已知饱和（或部分饱和）岩石的纵波速度和横波速度的情形

不管用测量还是用计算的方法，如果得到饱和（或部分饱和）岩石的纵波速度和横波速度，则可以推导出后向Gassmann方程Kd，形式如下：

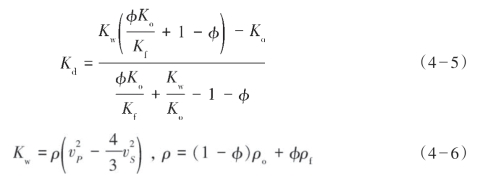
式中，Ko和Kf分别为岩石矿物颗粒的有效体积模量和孔隙流体的有效体积模量；ρ、ρo、ρf分别为岩石、固体矿物颗粒、孔隙流体的平均密度；φ为岩石孔隙度。(www.xing528.com)

② 已知饱和或部分饱和岩石的纵波速度而缺少横波数据的情形

当已知饱和或部分饱和岩石的纵波速度而缺少横波数据时，计算所需的输入参数是不够的，需要补充输入参数。补充参数方法可利用前人提出的经验关系，如纵、横波速度关系等。

（3）Xu-White模型法

Kuster和Toksöz方程是在假设孔隙度足够小的情况下推导出来的，Xu和White应用微分等效介质（Differential Effective Medium，DEM）的方法克服了这种限制。首先把孔隙空间分为很多套，每套孔隙均满足Kuster和Toksöz方程的条件。从坚固岩石开始，运用Kuster和Toksöz方程计算在基质上加一小套孔隙的有效介质，然后把结果作为下次计算的基质，如此重复，直到总的孔隙体积都加到岩石上。

Keys和Xu将基于DEM理论的Kuster和Toksöz方程转化为求解线性常微分方程组的问题，得到了泥质砂岩干岩石体积和剪切模量的简单解析表达式：

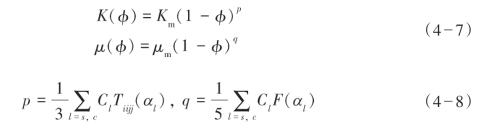
式中，K（φ）和μ（φ）分别是孔隙度为φ时的干岩石体积和剪切模量；Cl是砂岩和页岩占岩石基质的体积百分比；Tiijj（αl）和F（αl）参见Kuster-Toksöz（KT）模型部分。初始基质的模量计算采用下述方程：

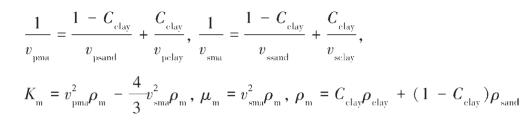
式中，Cclay为泥质含量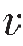；psand和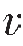pclay分别是砂和泥的纵波速度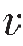；ssand和sclay分别是砂和泥的横波速度；ρsand和ρclay分别为砂和泥的密度；Km、μm和ρm分别是岩石骨架的体积模量、剪切模量和密度。用这种方法计算泥质砂岩的干岩石模量，需要已知砂、泥的基质纵、横波速度和密度等。在缺乏岩心的实验室测量数据时，这种方法是可行的。

（4）经验公式法

① Geertsma和Smit根据测量得到了一个可适用于纯砂岩的干岩石体积模量Kd与岩石基质模量Km和孔隙率φ的经验公式：

② Kief等参照一些实际数据，提出了如下的经验公式：

③ Nur基于临界孔隙度φc的概念，提出了如下线性的模量与孔隙度的关系：

④ Han依据实验数据，提出了如下的关系（D为经验系数）：

⑤ Murphy等通过对气饱和纯石英砂和砂岩样品的超声波测量数据（测量有效压力为50 MPa）的统计分析发现，干岩石骨架模量表现出对孔隙度的明显依赖性，并给出了最佳经验拟合公式。当φ≤0.35时，有

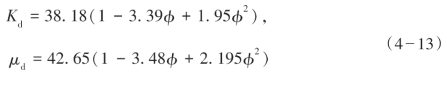
当φ>0.35时，有

上述二式对于泥质砂岩构成一个上边界。

⑥ Han-Eberhart-Phillips（HEP）模型是Eberhart-Phillips利用Han的实验室测量数据，运用回归算法得到的。这个模型显示出模量是孔隙度、有效压力和泥质含量的函数。有效压力是围压跟孔隙压力的差值。干骨架体积模量的表达式如下：

当φ＝0.0时，岩石骨架体积模量为：

类似地，剪切模量的表达式如下：

回归系数如表4—1所示：在回归系数中，数值单位是GPa。

表4—1　Han-Eberhart-Phillips（HEP）模型回归系数

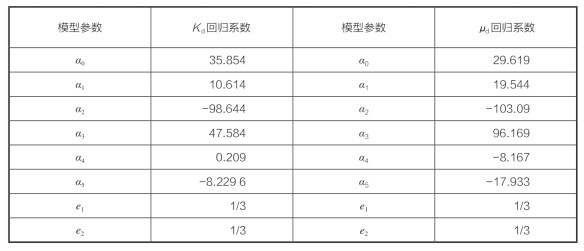
毫无疑问，最简便的方法是统计法或称经验公式法，特别是当工区内无测井岩心资料以及岩石物理实验资料时，该方法具有较大的优越性。但遗憾的是，现有的可以利用的经验公式很少，而且大多是针对纯石英砂岩提出的，公式中仅考虑了孔隙度的影响，从而大大限制了这一方法的应用。