地下局部角度域分解技术，提升页岩气地震勘探效果

1.全方位地下角度域波场分解与成像原理

该方法也遵循各向同性/异性地下模型局部角度域成像与分析的基本原理。成像系统涉及两个波场：入射波场和散射波场（反射和绕射）。每个波场可以分解为局部平面波（或射线），代表波传播的方向。入射和散射射线的方向，一般用它们各自的极角描述，每个极角包含两个分量：倾角和方位角。这里射线的方向指慢度或相速度的方向。成像阶段涉及合并众多代表入射和散射的射线对，每个射线对将采集的地表记录的地震数据映射到地下四维局部角度域空间，如图3—48所示，射线对法线的倾角υ1和方位角υ2，射线对反射开面的开角（或称为张角）γ1和开面的方位角 γ2（与正北方向夹角），这4个标量角度意味着入射与反射射线的方向与地下局部角度域的4个角度相关联。

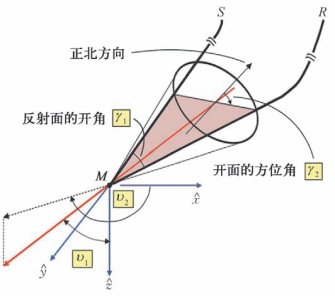
图3—48　地下成像点的入射与散射射线对及其地下局部角度域的4个角度示意图

从成像点向上到地表，射线路径、慢度矢量、旅行时间、几何扩散和相位旋转因子等可计算得到，这就形成一个成像体系，将地表记录地震数据映射到地下成像点的局部角度域。这个成像体系的优势主要在于能够构建不同类型的高质量角度域共像点道集（Angle-Domain Common-Image Gathers，ADCIG）来表示实际三维空间中连续的、全方位的、角度依赖的反射系数。

首先将地震记录数据分解到方向角度道集。注意到，对于每个倾角方向，地震数据同相轴对应的射线对具有相同视反射面方向但开角不同，用一个加权和的形式来表示。倾角道集包含关于镜像和散射能量的方向依赖信息。

在全方位地下局部角度域分解与成像体系中，对在全方位方向角度道集中获得的总散射场进行镜像（反射）和绕射能量分解，是技术核心。它基于对倾向性依赖的镜像属性的估算，该镜像属性衡量沿着3D方向道集在计算的局部菲涅耳带内反射能量的大小。而倾向性依赖的菲涅耳带则用预先计算的绕射射线属性进行估算，比如旅行时间、地表位置，以及慢度矢量。实际工作中，计算镜像反射方向道集的目的是为了从相应的地震方向道集中提取地下局部反射/绕射面的构造面属性（例如倾角、方位角和镜像性/连续性）。

全方位地下角度域波场分解：倾向（或方向）和反射角度道集。全方位地下角度域分解与成像方法包括三个主要过程：射线追踪、全方位角度域分解和最终成像。

射线追踪过程涉及从地下成像点向上到地面发射一系列扇形单程绕射射线。向上进行射线追踪的角度围绕背景反射界面的局部法向方向进行测算。每一条射线的有关属性，如旅行时间、射线坐标、慢度矢量、振幅和相位因子等，都要记录存储。

全方位角度域分解过程涉及构造入射和反射（绕射）射线对的组合。每一个射线对将采集地表记录的地震数据同相轴映射到地下4D局部角度域空间，即射线对法线的倾角和方位角，射线对所在开面的开角和开面的方位角（如图3—49所示）。这里所谓的射线对方向是指基于各向同性或各向异性的速度模型，即入射和散射的慢度方向已知，采用Snell定律计算的视法线方向（也叫作偏移倾向矢量）。当射线对方向的方向与物理反射界面的法向方向一致时，射线对的法向方向才是所谓的镜像方向。

如图3—49所示，炮点和检波点地面的4个坐标（炮点2个，检波点2个）可以用移位矢量（地下成像点的地面投影点和炮检中点之间的水平距离，也称为偏移孔径距离）和偏移距矢量（炮点和检波点之间的距离）来定义，而移位矢量和偏移距矢量均采用水平距离大小和方位方向来定义。理论上4个地表参数完全取决于地下4个局部角度域的角度，反之亦然。但是，倾向角度道集和移位矢量之间的依赖关系更强些，开角角度和偏移距矢量之间的依赖关系更浅一些，尤其是对于一些适度复杂的速度模型来说，更为明显。

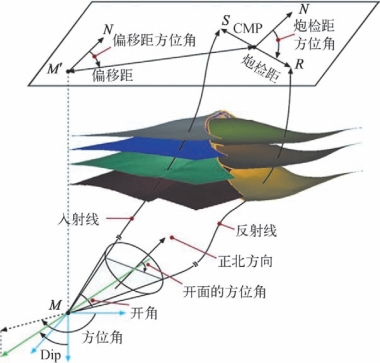
图3—49　基于地下到地面和地面到地下射线的空间映射

地表地震数据U到地下角度域的映射可以表示为：

式中，S＝｛Sx，Sy｝，R＝｛Rx，Ry｝分别为地表炮点和检波点的坐标；M为地下成像点。从地面5D地震数据向地下映射，将会生成7D角度域数据（每个地下界面反射点包括4个角度），这就意味着整个的映射过程需要大容量的计算机内存和海量磁盘空间存储计算结果。尽管上述映射（分解）过程对于提高地震成像和数据分析能力具有极大的价值，但是即使拥有最大的可利用的计算机资源，我们也认为不具有可行性。因此，提出将整个分解过程分裂为两个互补的角度域道集：方向角度域道集和反射角度域道集。在地下每个成像点，通过对其中两个角度进行积分，这些成像角度道集各自仅是两个角度函数。这里我们按照广义拉东变换成像方法的推导过程进行阐述。

2.倾向（或方向）角度道集和反射角度地震道集的求取

在方向角度地震道集中，地下成像点的反射/绕射率Iυ为射线对法向的倾角υ1和方位角υ2的函数：

式中，Kυ是倾向积分的核函数，

式中，Wυ是方向角度道集的积分权重，L是经过滤波和振幅加权的输入数据，

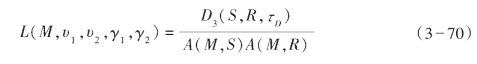
H是倾斜度因子，主要由开角γ1决定；这里用到的术语“绕射率”是指在非镜像方向的反射率。在反射角度道集中，地下成像点的反射率为开角γ1和开面方位角γ2的函数：

式中，Kγ是反射积分的核函数，

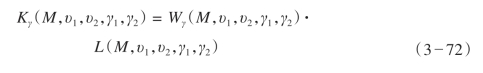
式中，Wγ是反射角度道集的积分权重，L是经过滤波和振幅加权的输入数据，如式（3—70）所示。在倾向和反射角度道集中，积分项都包含有核函数、倾斜度因子和球形面上的面积单元。对于倾向角度道集，积分界限从0到最大的开角γ1max，对于反射角度道集，积分界限从0到最大的射线对法线倾角υ1max，当然两个积分的上限角度都小于π。对于两个积分中的方位角维度υ2和γ2的积分界限均为全方位，即0到2π。式（3—68）和式（3—71）中倾斜度因子H定义为入射和反射射线慢度求和，即双程旅行时梯度的绝对值，它随开角γ1的增大而减小。

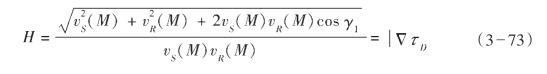
式中，S（M）和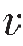R（M）分别是入射和散射射线在成像点的相速度。对于各向同性介质，这两个速度是相同的，则倾斜度因子H简化为：

(www.xing528.com)

也可以看到，当两个射线之间的开角变为直线，即γ1max→π，式（3—73）倾斜度因子变为：

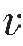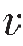进一步分析，当开角为直线时意味着入射和反射射线沿着同一个直线，对于一般的各向异性介质，在成像点它们的相速度相等，即S（M）＝R（M）。

这里，假设入射和反射射线均是地表到地下成像点，与成像点对应的采集地表坐标位置可表示为：

通过对联结成像点与给定炮点和检波点的单程波绕射射线进行追踪，获得这些采集地表的坐标位置。由于地表炮点和检波点位置的确定与背景速度模型和每个成像点的一组局部角度域的角度密切相关，使得这种输出驱动方法的实现十分困难。式（3—70）中的参数为：

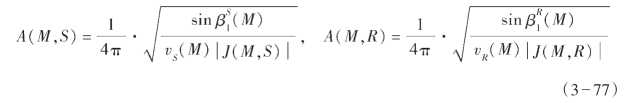
为格林函数的幅值，其中J为射线的Jacobian矩阵，

σ是沿着射线的积分变量，单位［σ］＝m2·s—1，而单位［J］＝m·s，［A］＝m—1，β1和β2分别是成像点射线出射方向的倾角和方位角。式（3—77）中数据滤波公式为：

其中ω是瞬时频率，是相位，定义如下：

U（S，R，ω）是频率域输入地震道，

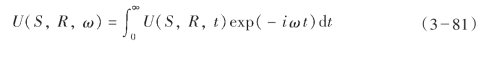
设时间域记录波场的单位是［U］，则频率域的波场单位则为［U］·s。式（3—79）中的因子B为点源的振幅，表示频率域的入射波场和相应的格林函数之间的常数比，单位是［B］＝［U］·m·s，这样滤波后的数据单位［D3］＝m—1·s—2。式（3—70）中振幅加权数据的单位为［L］＝m·s—2，与核函数Kυ和Kγ单位相同。式（3—68）和式（3—81）中估算的反射率的单位为［I］＝m—1。估算的反射率可以解释为I＝Rδ（s—s0），R是实际的反射率，δ（s—s0）是来自位于s0的反射体，是法向带符号的距离（s—s0）处的一维Diracdelta函数。

参数K（S，M，R）是KMAH指数，对沿追踪射线的焦散线个数进行记数，τD（S，M，R）是绕射叠加时间。焦散线是指沿着射线，那些Jacobian行列式消失的点。有两种情形焦散线较为独特：秩为2的Jacobian行列式（在规则点而不是3），即在射线管节面积缩变为一条线（KMAH指数增量为1）；秩为1的情形，射线管节面积缩变为一个点（KMAH指数增量为2）。式（3—81）是输入地震道从时间域到频率域、实数域到复数域的正傅里叶变换公式，根据傅里叶变换的性质，乘以iω相当于时间域导数的傅里叶变换。这样在没有焦散情况下，式（3—79）表示的逆变换将输入地震道的导数的傅里叶变换从频率域再反变换回时间域，若有焦散，通过式（3—80）修正相位再进行从复数域到实数域的变换，绝对的KMAH指数并不是必要的，但是除以4的余数则是必须要给的，当余数是0和2时，得到数据的导数，分别冠以原来的正负号和相反的正负号；余数1和3时，则得到的是导数的Hilbert变换，根据傅里叶变换和Hilbert变换之间的关系，分别冠以原来的正负号和相反的正负号。

式中，P是任意函数，这里P＝U/t，函数经过Hilbert变换仍然是时间域的函数。函数Wυ（M，υ1，υ2，γ1，γ2）和Wγ（M，υ1，υ2，γ1，γ2）是积分权重，与射线的照明度（射线数）成反比例关系。

图3—50给出了计算积分权重的方案。在对反射球面进行积分时，变化的反射双角度γ1，γ2（黑色虚线）是半径为βγ的圆形范围的中心，（红实线）是在此区域内多射线对的反射双角度。同样在方向球面进行积分时，变化的方向双角度υ1，υ2是半径为βυ的圆形范围的中心是该区域内多射线对的方向双角度。

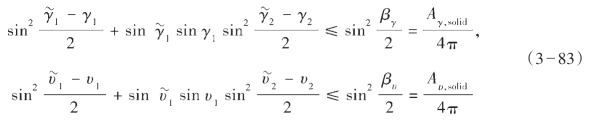
上式的右端项是积分范围的面积（立体角）与整个球面的比值。

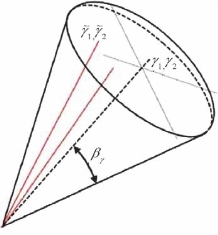
图3—50　立体角定义了反射球面上圆形范围

范围的中心方向见黑色虚线，在积分范围内，射线的起角度用红色实线表示

射线从成像点出射，均匀分布到各个方向，因此给定范围的面积与出射角度在范围半径内的固定射线数目是等价的。对于变化双角度的每个值，由于偏移孔径有限、观测系统以及背景速度模型的复杂性，在积分范围内的有些射线在一定的记录孔径内可以到达地球表面，而有些则不能到达。

3.全方位照明技术

关于地震资料成像，每个地下成像点在一个给定的孔径内，把所有输入数据进行叠加而获得。为了得到一个准确的成像效果，成像点需要从所有方向进行照明，因此需要从地表到地下进行映射，即将在地面的观测数据映射到局部角度域，来控制成像质量。为了判断成像效果的好坏，我们需要一个系统来分析有关映射的大量参数。

全方位照明技术的目的像一个放大镜来研究QC成像情况。照明技术作为一个挖掘地震数据属性的工具，用于深度成像，能够指导偏移成像的参数选取、分析、判断成像效果。该工具同时能够验证复杂构造、观测系统及不确定解释层位。

照明技术利用的数据为射线扇，该射线扇是通过交互射线追踪得到的。射线扇包括射线路径和射线属性。射线属性是沿着射线的传播计算参数的集合，包括位移距、偏移距、旅行时间、几何因子等，是地下角度的函数。