早期地震反演主要是利用地震走时信息，即基于地震射线理论的反演方法。从20世纪70年代开始，由于波场模拟技术和观测技术的发展，地震学家开始研究基于波动方程的反演方法，即波形反演。波形反演完全利用了地震记录中的振幅和走时（在频率域中为相位）信息，从理论上说可大大提高地震反演分辨率。由于受限于当时的计算条件，该方法在提出之后并未被广泛研究应用，而与此理论同时发展起来的偏移方法在近几十年却逐渐成为标准的地震处理流程。随着计算机技术的高速发展，原先无法实现的全波形反演逐渐成为可能；更由于地震偏移遇到了速度建模这个技术瓶颈，近年来，越来越多的研究人员重新开始投入波形反演的理论和应用的研究。波形反演可以在时间域和频率域两个数据域中实现。时间域方法有更长的研究历史，其算法核心是逆时偏移算法，随着近年逆时偏移技术逐渐被应用，时间域波形反演实用化研究也得到很大进步。频率域方法由于其理论上的优越性，受到更多的理论研究的关注。本书中针对近地表速度建模的early-arrival反演主要采用时间域波形反演方法，而针对复杂速度模型速度建模方法主要采用频率域波形反演方法。
1.波形反演基本理论
1）时间域和频率域
波形反演最早由Lailly和Tarantola等提出，其思想是建立一个反演目标函数使观测记录的波场数据和理论模拟波场的残差达到最小二乘。
Lailly最早提出波形最小二乘拟合反演在时间域的实现方法：作为模型扰动方向的目标函数梯度可以通过从源出射的正向传播波场和波场残差的逆向传播波场的互相关而得到，其算法与逆时偏移具有相同的算法结构，不同点在于逆时偏移逆时传播接收点记录波场，而波形反演逆时传播观测波场和模拟波场的残差。频率域波形反演公式最早由Shin推导得到。Pratt等人系统论述并实现了频率域波形反演。其思路是将波动方程变换到频率域后，对于某一单频点，时间域的逆时传播可以通过频率域波动方程的伴随方程实现，其优点主要表现在两个方面。
（1）对于某一单频点，频率域波动方程求解最后归结为一个大型稀疏矩阵方程的求解，在完成该稀疏矩阵的LU分解之后，不同炮点计算只是不同右端项的一个快速回代过程，如此对于多炮记录大大提高了计算效率。
（2）利用波场频率和模型尺度的内在联系，选择先低频后高频的反演策略，只需少数离散的频点即可完成反演，同时这种自然的多尺度实现方式减少了反演的非线性特征，提高了解的稳定性。
随着计算机技术的发展，多处理器多核并行集群的使用，时间域波形反演多炮正演很容易实现并行计算。而频率域正演求解大规模问题LU分解并行越来越困难，加速比无法随着处理器数量的增加而显著提高；更甚者，对于三维问题当前计算机内存很难满足直接LU分解的要求，其多炮快速正演的优点正在逐渐丧失。而单频多尺度的优点在时间域也很容易通过滤波方法实现。
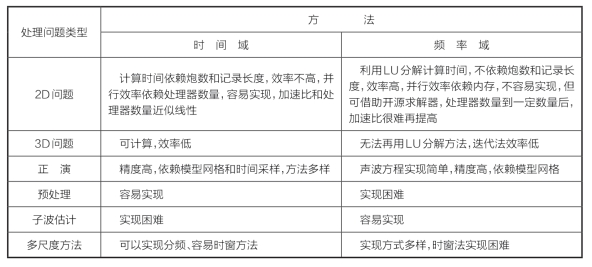
因此，有了对时间域波形反演和频率域波形反演孰优孰劣的问题。表3—1列出了两种实现方法在解决实际问题上的一些表现。由表可见对于两种方法的计算效率不仅仅依赖方法本身，主要还依赖计算机技术的发展。频率域方法的LU分解需要更多的内存，而时间域方法为解决多炮问题需要更多的处理器。时间域方法容易实现数据的预处理和与时窗相关的各种处理，但是很难实现子波估计，而频率域方法正好相反。
表3—1 波形反演时间域和频率域实现方法对比
2）时间域算法原理和实现
（1）时间域标量波动方程
时间域标量波动方程如式（3—45）所示。
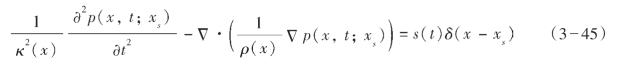
式中，κ（x）＝ρ（x）2（x）为体积模量，（x）为模型速度，ρ（x）为模型密度，x为模型网格位置；p（x，t；xs）为波场；s（t）为震源，δ（·）为Dirac函数，xs为震源位置。式（3—45）可使用有限差分、有限元等数值解法方便求解。本文采用16阶交错网格有限差分公式。式（3—45）的解可写成如下形式：
式中，G（x，t；x′，0）为Green函数，*为褶积。由式（3—46）得到的波场记为pcal，实际观测的波场记为pobs，时间域波形反演即求取使目标函数极小的模型m：
由式（3—47）推导得到：
(www.xing528.com)
式（3—48）为本文计算所用的速度校正梯度方向。由式（3—48）可见，波形反演校正梯度方向公式和逆时偏移成像具有完全相同的算法结构，不同之处在于波形反演将波形残差而非观测波场逆时传播，其成像条件为正传波场和逆传波场对时间一阶导数的零延迟互相关。计算得到梯度方向之后，可用如下的最速下降法公式更新模型。
式中，下标k为迭代次数；m为模型参数，对于我们研究的速度建模问题即速度；α为需要优化选取的校正步长。
（2）early-arrival反演
early-arrival特指地震初至后几个子波长度的波场信息。early-arrival反演就是只利用early-arrival信息的波形反演。Pratt最早在井间地震波形反演中使用了该方法。Sheng等研究该方法进行表层速度建模，研究认为early-arrival反演相比走时初至反演利用了更多的波场信息，反演结果具有更高的分辨率。另一方面early-arrival反演相比全波形反演，其目标函数局部极值较少，反演结果更稳定。early-arrival反演实现首先利用在时间域记录上切除early-arrival之外的地震信息，然后用时间域波形反演实现。
（3）频率域算法原理和实现
频率域单频标量声波方程可写成如式（3—50）所示形式：
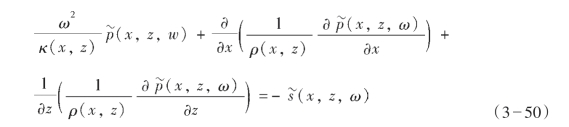
式中，ω为频率，κ为体积模量，ρ为密度，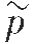
为频率域波场，
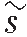为单频震源形式。利用有限差分或者有限元法求解上式可简化为
由于矩阵A只和频率和模型参数相关，所以对于同一频率多炮数据具有相同的矩阵A，对矩阵S进行LU分解有
利用公式（3—52）正演多炮记录，算法时间复杂度和炮数无关，大大提高了多炮数据的正演计算效率，为频率域反演打下了良好的基础。
（4）模型试算
为了验证波形反演结果对复杂近地表模型的建模效果，这里对Marmousi模型进行了试算。选取模型表层一段，由一组逆冲断层构成，结构复杂，常被用来作为深度偏移方法的测试模型，该模型最低速度为1 500 m/s，最高速度为5 500 m/s；原始模型网格间距dx＝12.5 m，dz＝4 m；网格数nx＝737，nz＝750。试算对模型进行重新采样，横向网格间距和网格数不变，纵向重采样后dz＝12.5 m，nz＝240。重采样使用su软件中的unisam2命令。模拟数据观测系统为炮距50 m，共计184炮，全排列接收。
为了突出对比表层速度建模效果，用ximage命令显示最低速度1 500 m/s，最高速度2 200 m/s。图3—36显示了反演结果，其中图3—36（a）显示了真实Marmousi模型的表层结构，图3—36（b）为走时层析反演的初始速度，是一个1 500 m/s ～500 m/s线性变化模型，图3—36（c）为利用时间域波形反演方法反演早震数据的结构，由图可见，波形反演精细刻画了真实速度模型的表层结构，具有很高的反演分辨率。
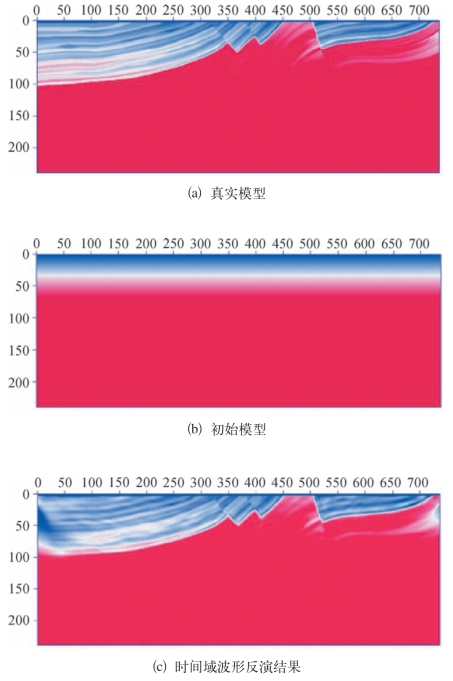
图3—36 Marmousi模型表层反演结果
频率域反演算法：从线性变化初始模型开始，应用单频顺序反演频点：0.3 ～18 Hz，频率间隔0.3 Hz，共计60个频点，每个频点最多迭代10次，如图3—37所示。
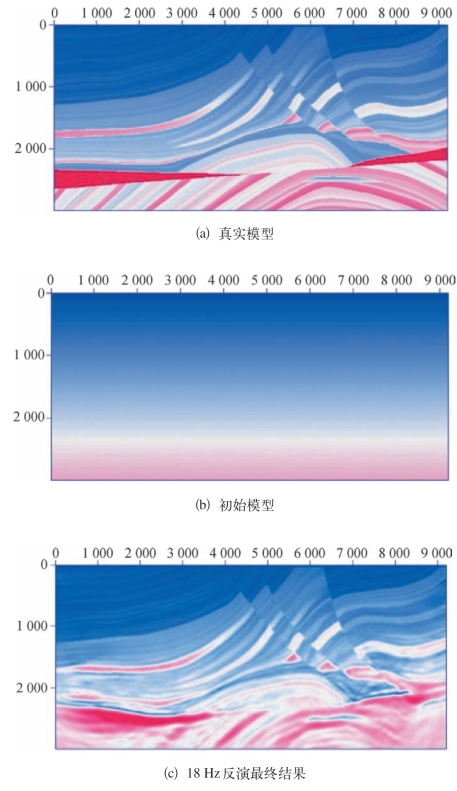
图3—37 Marmousi模型波形反演结果
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
